November 2012
Intermediate to advanced
794 pages
22h 9m
English
book
Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications
by John J. Shynk
Content preview from Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
9.21 PROPERTIES OF LS ESTIMATORS
In this section, we present some properties of the weighted LS estimator in (9.315) using matrix a in (9.311).
9.21.1 Minimum 
Substituting the WLS estimator into (9.313) gives
(9.347)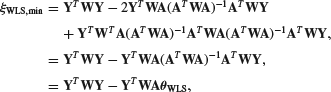 
where a symmetric weighting W = WT has been assumed. Substituting the LS parameters causes the third term in the expansion to cancel, and the last expression has 
reinserted after no further simplification is possible. A plot of the LS cost function 
for Example 9.44 with W = I is shown in Figure 9.17(a). It has a convex quadratic form, and the minimum is close to 
. Note that 
is not an ensemble quantity; it is a function of the samples so that the plot would change with different outcomes for X and Y. However, for large N, the basic shape and location of the minimum are as shown in the figure.
FIGURE 9.17 LS cost function for Example 9.44. (a) Nonsingular AT A. (b) Singular ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.