Chapter 4. Developing a Rigorous Approach Toward Problem Solving
Imagine that you have spent the last few months mentoring a friend who is in the early stages of a career in software development.
Your friend Emma started her first programming job about a year ago, and was mostly self-taught before then. Determined to gain experience as quickly as she can, Emma occasionally asks you for help whenever she hits a rough patch in her work.
In the last few weeks, Emma has noticed she seems to do well whenever she is working on well-defined tasks, but struggles when working on problems that have lots of fine-grained details that need to be sorted out before they can be solved.
Recognizing this stumbling block, Emma asks if it’d be worth trying out some programming puzzles as practice exercises.
You mull this idea over for a moment. Puzzles often needlessly complicate implementation details, represent data in inconvenient ways, and can be difficult to validate until all of their rules have been properly sorted out. This makes them awkward to use for developing practical coding skills, but perfect for exploring general problem solving techniques.
You find a puzzle you think Emma might like. She gets to work on it, while you stick around to help her out with any questions she has along the way.
In this chapter…
You will learn several straightforward tactics for breaking down and solving challenging problems in a methodical fashion.
Begin by gathering the facts and stating them plainly
Emma begins by reviewing the problem description for Counting Cards,1 the puzzle the two of you will be working on today. She finishes reading it in five minutes, which surprises you. You ask her to share her thoughts on it:
Emma: I get the basic idea behind this puzzle, but I’m not sure how to get started.
You: That’s OK. Try explaining what you know so far, and let’s see how far that gets us.
Emma: There’s a game transcript from some card game, and it lists out the different actions each player takes on their turn. You’re supposed to track the flow of cards as the game progresses, in order to figure out what’s in a particular player’s hand at the end of each round.
You: Yep, that’s my understanding of the problem, too. What do you think the challenging parts of solving it will be?
Emma: Well, you don’t have full information about what cards are in play. So I guess you’d need to use some sort of process of elimination to figure out what is in everybody’s hands? This is where I start drawing a blank.
You: Now that I think of it, this problem is probably complicated enough where just reading its description might not get us far. How about if we go back and take some notes on some of its key details, and see what that turns up?
Emma: If you think that would help, sure. Let’s do it.
Sifting through the noise in order to find the signal is a necessary first step whenever you’re working on a complicated problem. Rather then getting into a boring lecture on that topic, you attempt to demonstrate this to Emma by example.
You read the puzzle description out loud while she jots down notes, and then you swap roles and repeat the process. After you’ve finished reviewing and combining your notes, the basic details of the card game begin to take shape:
-
The game is played with a single standard deck of playing cards.
-
There are four kinds of actions that can happen on a player’s turn: drawing a card, passing a card to another player, receiving a card from another player, or discarding a card.
-
There is no apparent limit to the number of cards that can be drawn, passed, received, and discarded in a single player’s turn.
-
Once a card is discarded, it is out of play for the rest of the game.
The game transcript lists out the various actions taken on each player’s turn, but the amount of information provided varies for each player:

The expected output for the puzzle is a list of the cards in Lil’s hand at the end of each round. In order to generate this list, it’ll be necessary to try out the various sequences of moves provided for each of her turns, and then figure out which sequence is the correct one. This is the process of elimination that Emma mentioned earlier; all that remains is to figure out how to implement it.
Emma takes a few minutes to look over her notes and think about the problem. Then, in a flash of insight, she finds a foothold that will be good enough to get started with:
Emma: Oh, I see! If we track what we know about where each card is supposed to be, then we can eliminate sequences of moves that would lead to impossible outcomes… like when someone draws a card that has already been discarded, or attempts to pass a card that we know is actually in someone else’s hand.
You: Yep. It’s worth noting that for the full challenge, the process of elimination won’t be quite so straightforward, but your basic idea is exactly right.
Emma: I think I need to study the problem a little more to understand where those complications might come up. But I’ve looked over some of the practice data sets for the puzzle and I think I understand them now. How about if we start with those and see how far I can get with what I already know?
You: Sure! That sounds good.
Before this point, the problem description was just a sea of meaningless details and its input files were made up of cryptic symbols that resisted interpretation. But now with a sense of the end goal in mind and a glimpse of the path that might get her there, Emma sees the problem in a whole new light.
Work part of the problem by hand before writing code
You remain silent for a few moments while Emma reviews the first practice data set. This one is mostly meant to introduce the syntax and basic structure of the game transcript, so it only contains a single, valid sequence for each of Lil’s turns:
Shady +?? +?? +?? +?? Rocky +QH +KD +8S +9C Danny +?? +?? +?? +?? Lil +8H +9H +JS +6H Shady -QD:discard -2S:discard Rocky -KD:Shady +7H Danny -QC:Rocky +?? +?? Lil -6H:Rocky -??:Shady -8H:discard +?? -10S:discard +?? * -JS:Shady +10S +QS Shady +KD:Rocky +??:Lil -KD:discard -??:Lil Rocky +QC:Danny +6H:Lil -9C:Danny -6H:discard -7H:discard +3D +3H Danny +9C:Rocky -AD:discard +?? Lil +??:Shady +?? -??:Danny -??:Shady +?? * +AH:Shady +8D -8D:Danny -QS:Shady +8C Shady +??:Lil -7S:discard +?? -10H:discard Rocky -QH:Lil +5D -8S:Shady -3H:discard -QC:discard Danny +??:Lil +?? +?? -??:Lil -3S:Rocky -??:Shady Lil +QH:Rocky +??:Danny -AH:Rocky -QH:discard * +4D:Danny
Ten minutes later, Emma breaks her focus and signals that she needs some help:
Emma: I’m having trouble figuring out how to process this file.
You: Do you mean you don’t understand the actions themselves, or that you don’t know how to write the code to parse the file?
Emma: The latter. For example, I know that things like
+QHmean “draw a Queen of Hearts” and that-??:Shadymeans “pass an (unknown) card to Shady”—but I’m not really sure how best to model this data.The format for the possible sequences on Lil’s turn are a bit confusing to me, too. I know that the lines with the asterisks are meant to fill in the
??parts of Lil’s turn, but it’s not obvious to me how to write the code to merge them together.
You: To be honest, I’m not sure how to model this data yet, either. I usually work through a problem manually for a bit before thinking about how to write the code; it helps to see the moving parts before getting bogged down in implementation details.
Let’s do a step-by-step review of the game transcript, and see where that gets us.
Emma reads off the actions one by one, while you manually update a table that lists the state of each player’s hand. After completing the initial draw and the first full round of play, you end up with the following table:
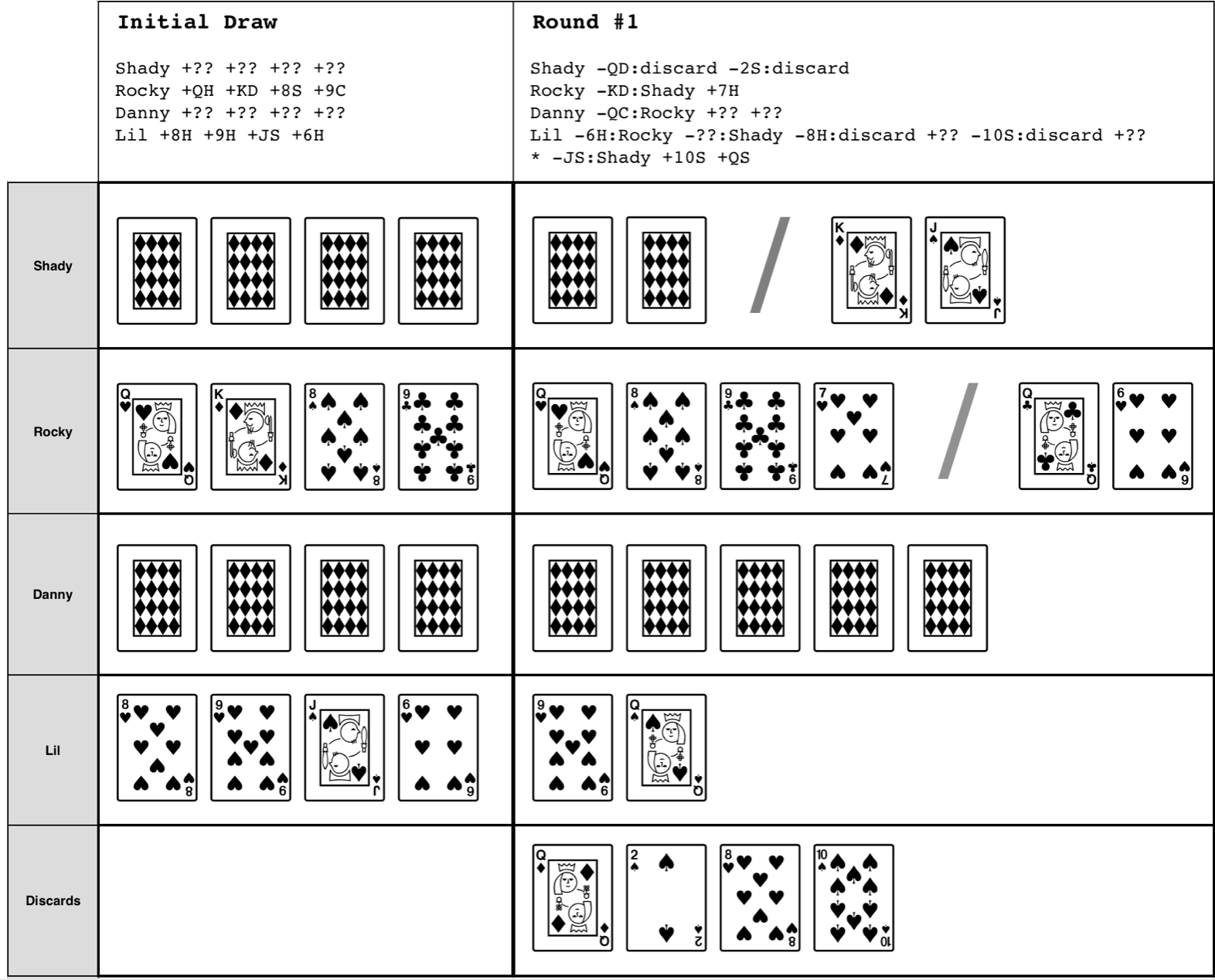
After you take a closer look at the table, the underlying structure of the problem becomes a bit easier to see:
-
A hand is a collection of cards assigned to a player, sorted in insertion order.
-
A hand may contain cards that have not been revealed yet.
-
Passing cards is a two-step process that isn’t finished until the receiver’s turn.
-
A discard pile is an append-only collection of revealed cards.
Using these basic ideas as a guide, Emma works on building some code to
model the hand and discard pile concepts. She begins by writing some
functions to match the various kinds of actions in the input files, so
that something like +QC becomes hand.add("QC").
In the process of coding up these models, Emma discovers that updating a
player’s hand involves more than just adding and removing
elements from a collection. For example, the behavior of the discard()
function depends on whether the card has been revealed yet or not, bringing up the question of how unrevealed cards ought to be
modeled.
Several other small “gotchas” like this come up as Emma works and she starts to get frustrated. But when you remind her that working the problem by hand was only about figuring out the big picture ideas, she realizes that it’s normal to hit some rough patches when sorting out fine-grained details in code.
Emma works through a few more edge cases that weren’t easy to spot when working the problem by hand. Eventually, her code starts working as expected in isolated tests, so she manually translates the game transcript from the first sample data set into function calls on her models.
Emma runs her script and is pleasantly surprised when it produces the correct output on the first try. This small win is important because it will keep her motivated as she works through the rest of the puzzle.
Validate your input data before attempting to process it
Emma turns her attention to the second practice data set:
Lil +5C +2H +8H +6D Shady +QH +AC +7C +2D +8C +3S -??:Lil Rocky +KS Danny +4H discard +4D +7D +JS +6S +6H +2C +5D +3C Lil +??:Shady -6D:discard -??:Danny +?? +?? * +8H:Shady -2H:Danny +JD +2D * +8C:Shady -8C:Danny +JD +4S * +QH:Shady -2H:Danny +7D +AS * +AC:Shady -8H:Rocky +AS +8D * +8C:Shady -2H:Danny +10H +9H +4C * -8H:Danny +8C:Shady +4S +AS
Noticing the small differences between how this file is formatted and how the first sample file was laid out, she returns to the problem description to read the notes about what this sample is for:
This file represents one round of the game immediately before Lil's turn. In this sample, you know what's currently in each of the players' hands and what's in the discard pile. Here there are six possible branches, only one of which can match Lil's actual moves. See if you can determine which is the correct set of moves, and deduce the cards in Lil's hand at the end of the round. Note that the invalid branches in this sample cover many (but not all) of the corner cases you're likely to encounter in the main puzzle.
Emma tells you that she plans to begin by walking through the transcript and listing out all the cards in play, similar to how you approached the first data set.
This is a good idea, but there is something else that is important to look at first. You ask her to review the branch syntax to make sure that she fully understands how it works before proceeding with her plan.
To test her assumptions, Emma constructs a table with the fully expanded
turn instructions for each branch. In theory, this should just be a
matter of matching up any action with a ?? to the corresponding action
in each branch. In practice, it turns out that not all branches are
properly formed:
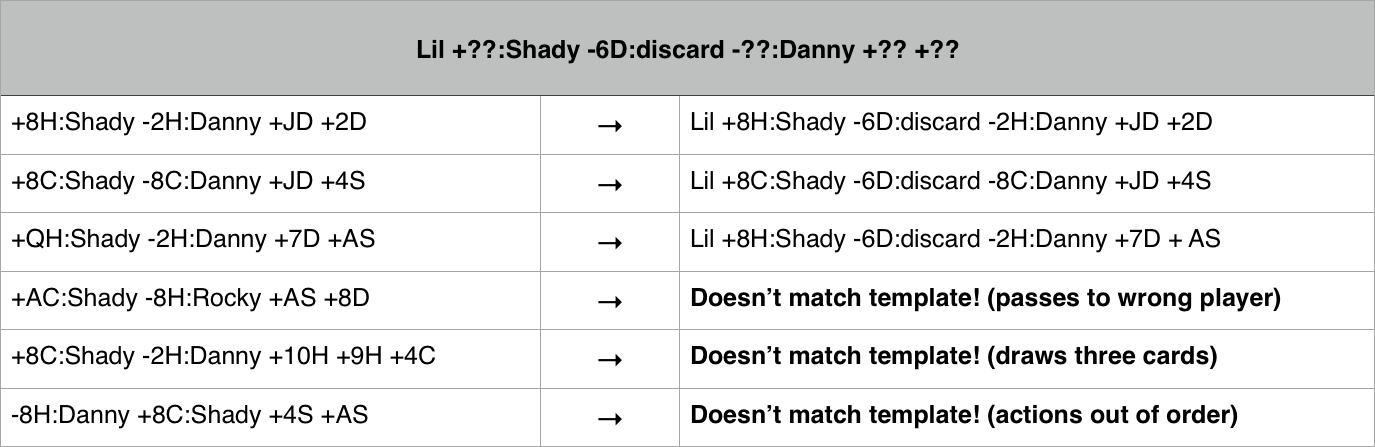
Emma is surprised by this discovery. The two of you talk a bit about it because there is an important lesson to be learned here:
Emma: This feels like complication for the sake of complication. It doesn’t really add anything to the interesting part of the problem, so why would the puzzle’s author want us to jump through this extra hoop?
You: Well, I’d argue that it was most likely meant to make the puzzle a little more realistic. Raw data is usually messy, so the idea of having to process this sample before we can make use of it is only natural.
Emma: So are you saying that you knew the sample data would have problems, and that’s why you had me hand-verify it?
You: No, it’s just a good habit to get into; otherwise, you can easily write programs that take garbage in, and spit garbage out.
As soon as you identified a single branch that wasn’t in the correct form, you discovered the need to validate all of the branches. It only took you a few minutes to find this issue, so it was well worth the initial time investment.
There are certain cases where assuming that data is in a valid format is a safe bet, but if in doubt, it’s better to err on the side of caution.
Emma: OK, I think I understand that now, thanks.
In order to write a validation method, Emma needs to process Lil’s turns
and extract the actions with ?? in them. You suggest converting this
data into an array of arrays, to capture its basic structure in code:
Lil +??:Shady -6D:discard -??:Danny +?? +?? [[:receive, "Shady"], [:pass,"Danny"], [:draw], [:draw]]
From here, the same translation can be applied to each of the branches. If doing so produces an identical structure, the branch is at least in the correct form. If it produces a different result, it can immediately be marked as invalid.
Emma walks through the six possible branches in the sample file and manually translates the lines of text into the format you suggested. In doing so, she finds that the first three exactly match the structure of Lil’s turn, while the last three all produce non-matching structures.
The two of you work together to implement a validation method based on these ideas, and then use a similar approach to build a parser for the game transcripts. Emma learns some interesting text processing tricks along the way, but they’re not the focus of the lesson. She quickly shifts her attention back to the problem at hand.
Make use of deductive reasoning to check your work
With the improperly formed branches weeded out, the next step will be to logically verify the three remaining branches to figure out which one lists the correct sequence of moves. At this point, a sketch of the state of each player’s hand is exactly what’s needed, so Emma puts one together:2
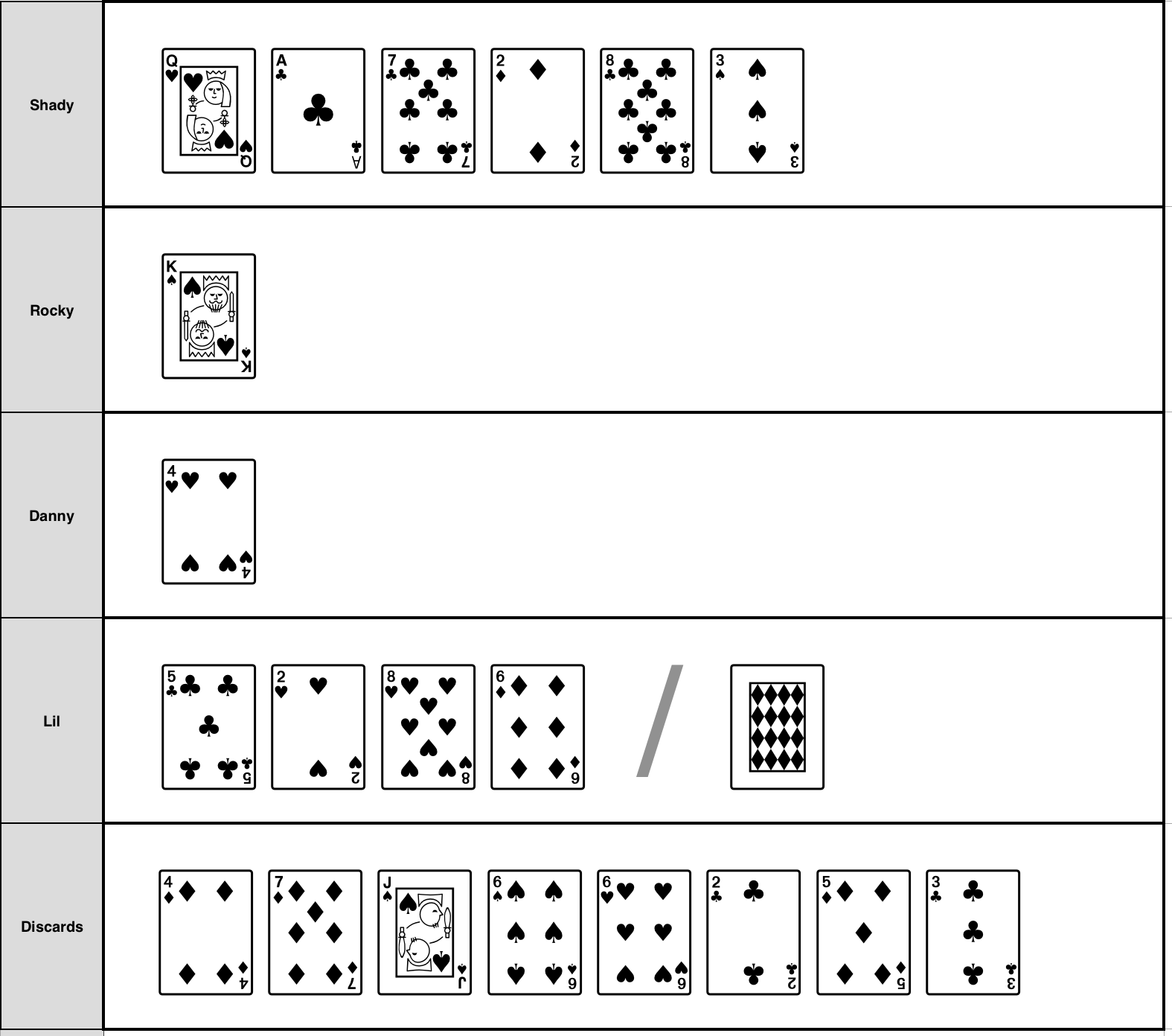
Using the table of moves she produced earlier, Emma walks through the branches one by one and hand-verifies them while talking out loud:
Emma: The first branch is
Lil +8H:Shady -6D:discard -2H:Danny +JD +2D.Right away, I can see this is impossible. Because Lil already had the Eight of Hearts in her hand, there is no way that Shady could pass it to her in this turn.
You: That’s right! How about the next one?
Emma: The second branch is
Lil +8C:Shady -6D:discard -8C:Danny +JD +4S.Shady does have the Eight of Clubs, so there’s no reason she couldn’t pass it to Lil. Lil does have the Six of Diamonds, so discarding it would be a valid move. If Shady did pass the Eight of Clubs to Lil, then Lil could definitely pass it immediately to Danny, so no problems there either.
Finally, both the Jack of Diamonds and the Four of Spades don’t appear in anyone’s hand or in the discard pile, so there’s no reason why Lil couldn’t draw them from the deck. I’d say this branch is possible.
You: Sounds right to me. Because this data set only covers a single round of the game, we know (in theory) that the third and final branch is impossible without even looking at it. But just to check our work, we should verify it nonetheless.
Emma: OK, the third branch is
Lil +8H:Shady -6D:discard -2H:Danny +7D +AS.I see immediately that this has the same problem as the first branch; it’s impossible for Shady to be passing the Eight of Hearts because it’s already in Lil’s hand.
You: Nice work; it looks like we’ve got our answer. Now it’s time to move on from the practice data sets and start exploring the real challenge.
Author’s note
In the process of constructing this dialogue, I had made a transcription error that incorrectly led me to believe the second branch was invalid. It wasn’t until I wrote the “let’s check just to be sure” line that I caught my error. Embarrassing, but a funny enough coincidence that proves the point of this section.
Solve simple problems to understand more difficult ones
Working with two practice data sets has given Emma a solid starting point for solving the puzzle, but the difficult part will be combining these ideas together in order to process a full game with many branches per round.
Before going any further, you check in with Emma to see what her plans are for the remaining work to be done:
You: Can you walk me through what you plan to do next?
Emma: Sure. The challenge data set is basically a combination of the two samples we’ve seen so far, right?
You: That’s right. The first data set showed you what a transcript of game actions looked like, and from that you were able to start tracking everyone’s hands as the game played out.
The second data set showed you how to narrow down the possible sets of actions on Lil’s turn until you found the only branch that would not lead to an impossible move.
Emma: OK. I should update the code so that whenever we get to Lil’s turn, we’ll first eliminate any branches that aren’t in the proper form.
From there, we take one branch at a time and run its sequence of actions. If we can run all the actions listed in the branch without running into an impossible move, we will know we found the right branch.
What I don’t understand is why the challenge data set is so small. With only three possible branches for each round, and only five rounds to go through, wouldn’t that at most require checking 15 different possibilities? That seems really easy to do by hand.
You: Nope, there are actually 243 different possibilities. To understand why, go ahead and check out the three branches for Lil’s first round in the challenge data set. Use the same process of elimination we did earlier, and see where it gets you.
Emma reviews the first several lines of the challenge data set:
Shady +?? +?? +?? +?? Rocky +5S +QH +6H +JC Danny +?? +?? +?? +?? Lil +7C +3S +8D +9H Shady -4H:discard -??:Danny +?? Rocky +10D -10D:Danny +4S +2D -4S:discard -JC:Lil Danny +??:Shady +10D:Rocky +?? +?? +?? -4D:discard Lil +JC:Rocky +?? -??:Shady +?? * +JH -7C:Shady +10C * +JH -8D:Shady +9S * +JH -8D:Shady +10C (... next four rounds would follow here ..)
After scribbling notes down for a few minutes, Emma notices what you had hoped she would: without looking beyond the first round, it is impossible to eliminate any of the three branches listed for Lil’s first turn.
When she does look ahead, Emma starts to see how a particular branch choice might lead to an impossible move on a future turn, but eliminating possibilities ends up taking much more effort than she originally thought it would. Discovering a dead end can mean playing out the game all the way to the last line of the transcript, making this data set much more difficult to process by hand than the practice sets were.
With this detail of the puzzle clarified, there is a whole lot more to think about. Emma takes a short break to process it all, while you think through how you might be able to help her get through this tricky part of the problem.
When Emma returns, you show her a simplified problem that you’ve constructed to help her understand the work that needs to be done:
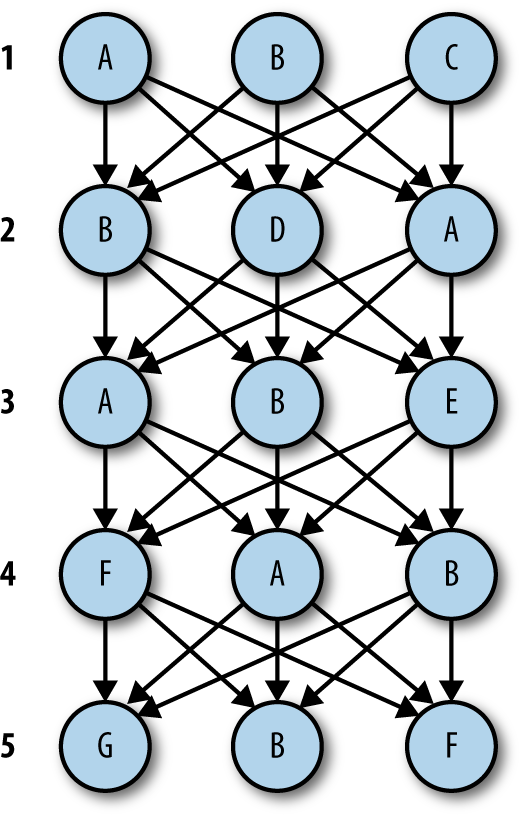
Emma: Wow, that’s a lot of arrows! What am I looking at here?
You: Well, it’s basically an idealized form of the Counting Cards puzzle. I know it looks a bit abstract, but I promise it is directly relevant to solving the problem.
It consists of five sets of letters. The goal of this puzzle-within-a-puzzle is to pick exactly one letter from each set so that you end up with
{A, B, C, D, E}in the end. The order that you collect the letters in doesn’t matter, so long as you pick up all five.The arrows represent all the possible sequences of choices you could make if you were choosing letters blindly. It amounts to a total of 243 distinct paths from top to bottom.
Emma: Ah, I see what you did there. The five sets represent the five rounds of the card game, the three choices per set represent Lil’s branching turns, and the 243 possibilities are all the different combinations that can be made of those branches.
Seeing the structure of the problem definitely helps, but I’m still a little lost on how to translate this into implementation details. Can you give me a few more hints?
You: Sure. Imagine that you don’t know much about how everything in this graph is laid out, but you do know the goal: to get a set that (when sorted) is equal to
{A, B, C, D, E}. From that, you can start to derive rules for when you know you’re on a dead-end branch. Can you think of one?
Emma: I see some other letters in the sets, like
FandG. If we ran into one of those, we’d know it wasn’t a valid choice, and so we could eliminate the branch straightaway.
You: Yep, that’s roughly similar to when we reject branches in the card game that don’t match the structure of Lil’s turn. Can you find another constraint that’s more subtle?
Emma thinks for a few minutes, and then realizes that if you ever happen
to pick the same letter from more than one set, it’s impossible to
produce the correct output. For example, if you chose the first elements
of the first three sets, you’d end up with ABA. With only two sets
left of letters to pick from, it’d be impossible to complete the full
{A, B, C, D, E} set.
You point out the similarity between this observation and the idea of making an “impossible move” in the card game, and Emma smiles as she begins to understand what you’re getting at.
You: At this point, we’ve simplified the puzzle to a graph traversal problem. We use a selection criteria to identify dead-end branches, and we keep iterating until we find the one path that gets us all the way to the end.
Emma: I understand the selection part, but I might need some help in figuring out how to iterate through the different paths.
You: Well, the data set is small enough where it’s probably not worth looking for some sort of fancy heuristic to narrow the search space. Instead, you could probably use a simple depth-first search.
Emma: So you mean: keep taking the left-most path until you hit a dead end, then jump one level up and try the next path, repeating that over and over?
You: Yep! Go ahead and look at the graph and tell me what the first few dead-end paths would look like.
Emma:
ABA, ABB, ABEF, ABEA, ABEB… Should I keep going?
You: Nope. You’ve successfully exhausted the
ABpath. The next step would be to go on toADand repeat the process, and so on from there.Now what I’d like you to do is write the program that solves this little puzzle. I can help you where needed, but it should be fairly straightforward.
It takes some effort, but Emma eventually gets her program up and running. When she’s done, she has a script that recursively walks through the graph, trying out the various different paths.
Emma runs her program, and then traces the path it outputs onto the original graph, producing the following result:
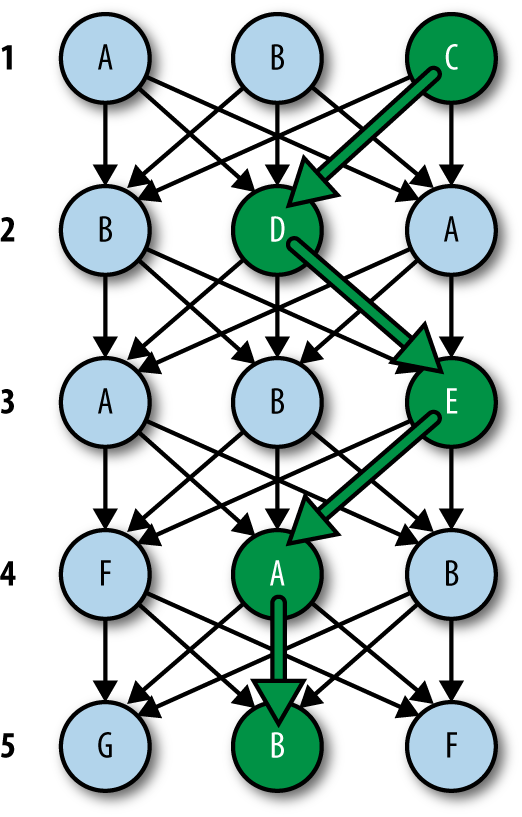
You: Awesome! You found the needle in the haystack. Now should we get back to the original puzzle and solve that too?
Emma: If you don’t mind, I think I’d like to solve the rest of this on my own. The stuff you’ve showed me so far has been super helpful, and I think I can keep applying it to sort out the rest of the puzzle.
You: Hey, that’s a great idea. I’m available to help if you need me, but as long as you’re feeling up for it, finishing it on your own will almost certainly be more rewarding. It also reminds me of the most important lesson from what we worked on today…
Emma: What’s that?
You: Real problem solving is often a solitary experience. You can get support from others, but in the end, you need to understand all the pieces of a problem for yourself in order to see how it all comes together. That’s the essence of what it means to think rigorously anyway: to understand something with a great deal of precision and detail.
Emma: That makes a lot of sense. And it seems like if you can take complicated problems and break them down like we did today, they become more approachable. Before it kind of felt like hitting a wall whenever I started working on a problem that I didn’t immediately understand, but I think I might be able to look at things differently now.
You: Really good to hear that. I won’t lie, this is something that we all need to remind ourselves of from time to time. But it seems like you definitely have the right idea. Good luck with the rest of the puzzle!
As you pack up your things, you look over and see Emma still hard at work. A puzzle that she had initially thought was totally beyond her reach has captured her interest and attention, and now she has a great chance at solving it.
You’ve made it to the middle of the book. Hooray!
Here’s another little riddle for you to solve, if you’re up for it…
Midway through the $tack, it’s time to unwind. A secret message is what you’ll find!
1 Counting Cards by Eric Gjertsen. The chapter does not assume you’ve read this problem description, but if you want a more immersive experience, go ahead and do that now.
2 The state of everyone’s hand is known with one exception: Shady passed a card to Lil, but that card has not been identified yet. That said, it must be one of the cards listed in Shady’s row.
Get Programming Beyond Practices now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

