Programming Collective Intelligence

Appendix B. Mathematical Formulas

Throughout the book I have introduced a number of mathematical concepts. This appendix covers selected concepts and gives a description, relevant formulas, and code for each of them.

Euclidean Distance

Euclidean distance finds the distance between two points in multidimensional space, which is the kind of distance you measure with a ruler. If the points are written as (p₁, p₂, p₃, p₄, ...) and (q₁, q₂, q₃, q₄, ...), then the formula for Euclidean distance can be expressed as shown in Figure B-1.

Figure B-1. Euclidean distance

A clear implementation of this formula is shown here:

def euclidean(p,q):
  sumSq=0.0

  # add up the squared differences
  for i in range(len(p)):
    sumSq+=(p[i]-q[i])**2

  # take the square root
  return (sumSq**0.5)

Euclidean distance is used in several places in this book to determine how similar two items are.

Pearson Correlation Coefficient

The Pearson correlation coefficient is a measure of how highly correlated two variables are. It is a value between 1 and −1, where 1 indicates that the variables are perfectly correlated, 0 indicates no correlation, and −1 means they are perfectly inversely correlated.

Figure B-2 shows the Pearson correlation coefficient.

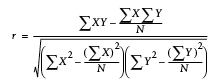
Figure B-2. Pearson correlation coefficient

This can be implemented with the following code: ...