Quantitative Risk Management: A Practical Guide to Financial Risk, + Website

10.1 Volatility, Triangle Addition, and Risk Reduction

As a guide for understanding how the risk of assets combine to yield the total portfolio risk, volatility and linear approximations are extremely useful. Volatility may not be the perfect measure of risk, but the intuition it builds regarding the often-nonintuitive aggregation of risk is effective, even invaluable.

The volatility of a portfolio is calculated from the volatilities of two assets according to:¹

(10.1a)

The cross term 2ρσ₁σ₂ means that the portfolio variance and volatility are not the simple addition of the position variances or volatilities. In fact, position volatilities combine like the legs of a triangle:²

(10.1b)

The two expressions will be equivalent when cos θ = – ρ:

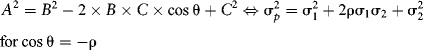
Consider the portfolio of $20M U.S. Treasury bond and €7M nominal of CAC equity index futures considered in Chapter 9, shown in Table 10.1.

Table 10.1 Volatility for Government Bond and CAC Equity Index Futures (reproduced from Table 9.7)

Based on Table 5.2 from A Practical Guide to Risk Management, © 2011 by the Research Foundation of CFA Institute.

In Figure 10.1, Panel A shows the combination of the two volatilities as the two legs of a triangle. ...