Quantum Physics For Dummies, Revised Edition

Chapter 3

Getting Stuck in Energy Wells

In This Chapter

• Understanding potential wells
• Working with infinite square wells
• Determining energy levels
• Trapping particles with potential barriers
• Handling free particles

What's that, Lassie? Stuck in an energy well? Go get help! In this chapter, you get to see quantum physics at work, solving problems in one dimension. You see particles trapped in potential wells and solve for the allowable energy states using quantum physics. That goes against the grain in classical physics, which doesn't restrict trapped particles to any particular energy spectrum. But as you know, when the world gets microscopic, quantum physics takes over.

The equation of the moment is the Schrödinger equation (derived in Chapter 2), which lets you solve for the wave function, ψ(x), and the energy levels, E:

Looking into a Square Well

A square well is a potential (that is, a potential energy well) that forms a square shape, as you can see in Figure 3-1.

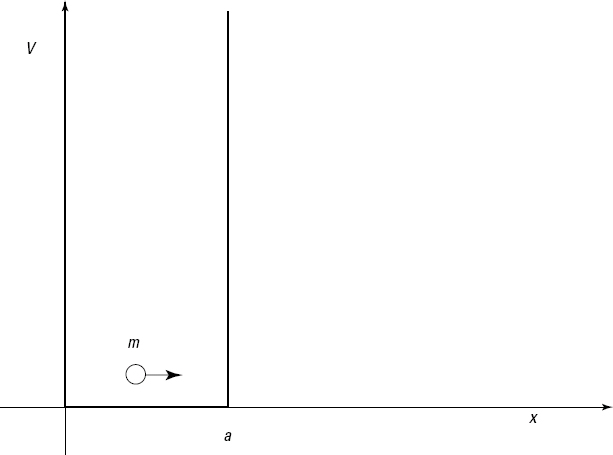
Figure 3-1: A square well.

The potential, or V(x), goes to infinity at x < 0 and x > a (where x is distance), like this:

• V(x) = ∞, where x < 0
• V(x) = 0, where 0 ≤ x ≤ a
• V(x) = ∞, where x > a

Using square wells, you can trap particles. If you put a particle into a square well with a limited amount of energy, it'll ...