January 2010
Beginner
634 pages
19h 50m
English
Content preview from R in a Nutshell
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
Correlation and Covariance
Very often, when analyzing data, you want to know if two variables are correlated. Informally, correlation answers the question “when we increase (or decrease) x, does y increase (or decrease), and by how much?” Formally, correlation measures the linear dependence between two random variables. Correlation measures range between −1 and 1; 1 means that one variable is a (positive) linear function of the other, 0 means the two variables aren’t correlated at all, and −1 means that one variable is a negative linear function of the other (the two move in completely opposite directions; see Figure 16-1).
Figure 16-1. Correlation
The most commonly used correlation measurement is the Pearson correlation statistic (it’s the formula behind
the CORREL function in
Excel):
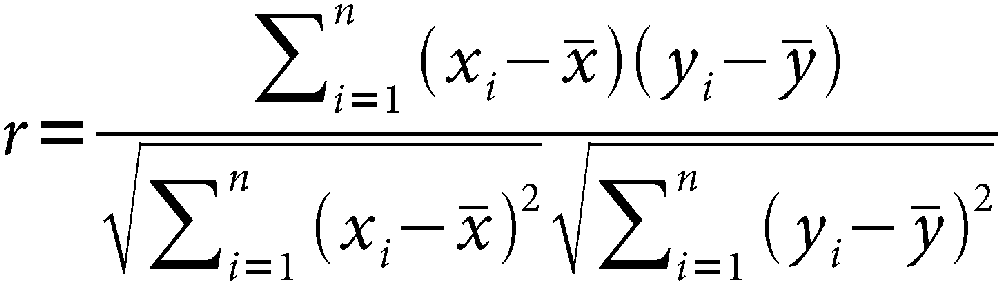
where x̄ is the mean of variable x, and ȳ is the mean of variable y. The Pearson correlation statistic is rooted in properties of the normal distribution and works best with normally distributed data. An alternative correlation function is the Spearman correlation statistic. Spearman correlation is a nonparametric statistic and doesn’t make any assumptions about the underlying distribution:
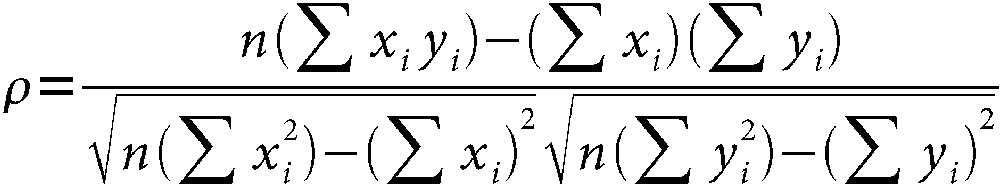
Another measurement ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.