Regression Analysis by Example, 4th Edition

CHAPTER 2

SIMPLE LINEAR REGRESSION

2.1 INTRODUCTION

We start with the simple case of studying the relationship between a response variable Y and a predictor variable X₁. Since we have only one predictor variable, we shall drop the subscript in X₁ and use X for simplicity. We discuss covariance and correlation coefficient as measures of the direction and strength of the linear relationship between the two variables. Simple linear regression model is then formulated and the key theoretical results are given without mathematical derivations, but illustrated by numerical examples. Readers interested in mathematical derivations are referred to the bibliographic notes at the end of the chapter, where books that contain a formal development of regression analysis are listed.

2.2 COVARIANCE AND CORRELATION COEFFICIENT

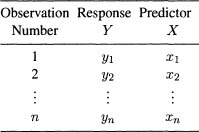
Suppose we have observations on n subjects consisting of a dependent or response variable Y and an explanatory variable X. The observations are usually recorded as in Table 2.1. We wish to measure both the direction and the strength of the relationship between Y and X. Two related measures, known as the covariance and the correlation coefficient, are developed below.

Table 2.1 Notation for the Data Used in Simple Regression and Correlation

On the scatter plot of Y versus X, let us draw a vertical line at and a horizontal line at , as shown in Figure 2.1, where

are the sample ...