RF and Microwave Engineering: Fundamentals of Wireless Communications

2.2 Maxwell's Equations

In the previous sections we reviewed basic electromagnetic field quantities for the static case. Now, Maxwell's equations provide a set of differential equations that describe the time-varying behaviour of electromagnetic phenomena in general. The field quantities in these formulas are real-valued vector functions of space and time t. (If—for instance—we look at the Cartesian coordinates of the electric field vector, the component in x-direction would read .)

Using Maxwell's equations we can calculate the electric and magnetic fields for a given initial field and a set of boundary conditions (initial boundary-value problem).⁹ Maxwell's equations exist in differential and integral form. In the following sections we will investigate both forms and focus primarily on their physical meaning and visual interpretation.

2.2.1 Differential Form in the Time Domain

Maxwell's first equation (Ampere's law) in differential form is given by

2.39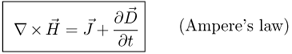

where is the current density in conductive media. It is therefore often called conduction current density . The expression has the ...