RF and Microwave Engineering: Fundamentals of Wireless Communications

4.2 Coaxial Line

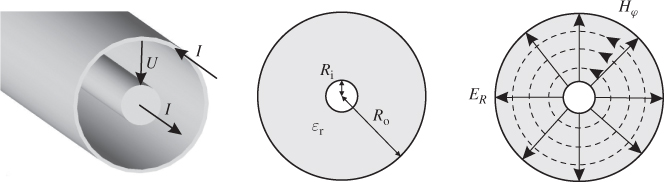
A coaxial line consists of two concentric cylindrical conductors (see Figure 4.2), where R_i and R_o are the inner and outer radius, respectively. The two conductors are separated by a homogeneous dielectric material with a relative permittivity of ε_r. The voltage U between the inner and outer conductor corresponds to a radial electric field strength E_R and the current I in the conductors produces a circulating magnetic field strength H_φ.

Figure 4.2 Geometry of a coaxial line and electric and magnetic field distribution of a TEM wave.

In the following sections we will derive the transmission line parameters of a coaxial line. The cylindrical symmetry of the problem allows a mathematically quite simple treatment using cylindrical coordinates. In our considerations we employ our knowledge of electromagnetic theory from Chapter 2 and the definitions from the transmission line theory in Chapter 3.

4.2.1 Specific Inductance and Characteristic Impedance

Let us consider a loss-less transmission line. We can calculate the characteristic impedance Z₀ from the inductance per unit length L′, the material parameters ε_r and μ_r and the light speed in vacuum c₀ (see Equation 3.69).

4.1

Technical transmission lines commonly use dielectric, non-magnetic materials. Hence, we set μ ...