Signals and Systems

7.7 CIRCULAR OR PERIODIC CONVOLUTION

If we convolve two finite sequences x(n) with y(n), we can determine the convolution sum. If x(n) and y(n) are periodic, the sequence x(n) and y(n– k) is of infinite length and hence the sum does not converge. Therefore, we get the infinite convolution which is absolutely meaningless. It is possible in such cases that for over one period. the convolution result gives the similar result of normal convolution. Figure 7.10 shows the sequences x(n) and y(n).

 

 

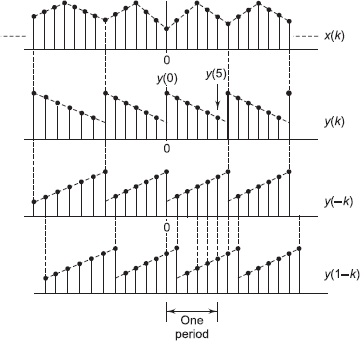
Fig. 7.10 x(n) and y(n)

 

We can write for one period of y(n)

 

 

Therefore, the value of y(0) which slips out the period enters at the left and hence ...