Signals and Systems

9.8.4 Solution of Non-homogeneous State Equation

In this case u (t) is taken into account.

Taking Laplace transform of Eq.(9.49), we get,

 

s X(s) – x(0) = AX(s) + BU(s)

 

∴      (sI – A) X(s) = x(0) + BU(s)

 

∴    X(s) = [sI – A] ⁻¹ x(0) + (sI – A) ⁻¹ BU(s)       (9.64)

 

Taking inverse Laplace transform of Eq. (9.64), we get,

 

x(t) = LT⁻¹[(sI – A)⁻¹ x(0) + (sI – A) ⁻¹BU(s)]

= LT⁻¹[(sI – A) −1 x(0) + LT⁻¹[sI – A) ⁻¹BU(s)]

 

Now  LT⁻¹[(sI – A)⁻¹x(0)] = ϕ(t) x(0) = e^Atx(0)

 

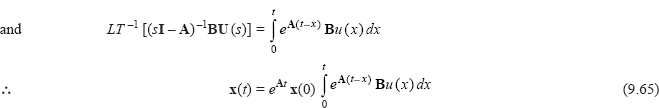
Eq. (9.67) represents the solution of non-homogeneous equation. It consists of (i) the term e^Atx(0) called homogeneous or free response and (ii) the term called forced ...