Speaking JavaScript

Chapter 11. Numbers

JavaScript has a single type for all numbers: it treats all of them as floating-point numbers. However, the dot is not displayed if there are no digits after the decimal point:

> 5.000
5

Internally, most JavaScript engines optimize and do distinguish between floating-point numbers and integers (details: Integers in JavaScript). But that is something that programmers don’t see.

JavaScript numbers are double (64-bit) values, based on the IEEE Standard for Floating-Point Arithmetic (IEEE 754). That standard is used by many programming languages.

Number Literals

A number literal can be an integer, floating point, or (integer) hexadecimal:

> 35  // integer
35
> 3.141  // floating point
3.141
> 0xFF  // hexadecimal
255

Exponent

An exponent, eX, is an abbreviation for “multiply with 10^X”:

> 5e2
500
> 5e-2
0.05
> 0.5e2
50

Invoking Methods on Literals

With number literals, the dot for accessing a property must be distinguished from the decimal dot. This leaves you with the following options if you want to invoke toString() on the number literal 123:

123..toString()
123 .toString()  // space before the dot
123.0.toString()
(123).toString()

Converting to Number

Values are converted to numbers as follows:

Value	Result
`undefined`	`NaN`
`null`	`0`
A boolean	`false` → `0`
	`true` → `1`
A number	Same as input (nothing to convert)
A string	Parse the number in the string (ignoring leading and trailing whitespace); the empty string is converted to 0. Example: `'3.141'` → `3.141`
An object	Call `ToPrimitive(value, Number)` (see Algorithm: ToPrimitive()—Converting a Value to a Primitive) and convert the resulting primitive.

When converting the empty string to a number, NaN would arguably be a better result. The result 0 was chosen to help with empty numeric input fields, in line with what other programming languages did in the mid-1990s.^[14]

Manually Converting to Number

The two most common ways to convert any value to a number are:

`Number(value)`	(Invoked as a function, not as a constructor)
`+value`

I prefer Number(), because it is more descriptive. Here are some examples:

> Number('')
0
> Number('123')
123
> Number('\t\v\r12.34\n ')  // ignores leading and trailing whitespace
12.34

> Number(false)
0
> Number(true)
1

parseFloat()

The global function parseFloat() provides another way to convert values to numbers. However, Number() is usually a better choice, as we shall see in a moment. This code:

parseFloat(str)

converts str to string, trims leading whitespace, and then parses the longest prefix that is a floating-point number. If no such prefix exists (e.g., in an empty string), NaN is returned.

Comparing parseFloat() and Number():

Applying parseFloat() to a nonstring is less efficient, because it coerces its argument to a string before parsing it. As a consequence, many values that Number() converts to actual numbers are converted to NaN by parseFloat():
```
> parseFloat(true)  // same as parseFloat('true')
NaN
> Number(true)
1

> parseFloat(null)  // same as parseFloat('null')
NaN
> Number(null)
0
```
parseFloat() parses the empty string as NaN:
```
> parseFloat('')
NaN
> Number('')
0
```
parseFloat() parses until the last legal character, meaning you get a result where you may not want one:
```
> parseFloat('123.45#')
123.45
> Number('123.45#')
NaN
```
parseFloat() ignores leading whitespace and stops before illegal characters (which include whitespace):
```
> parseFloat('\t\v\r12.34\n ')
12.34
```
Number() ignores both leading and trailing whitespace (but other illegal characters lead to NaN).

Special Number Values

JavaScript has several special number values:

Two error values, NaN and Infinity.
Two values for zero, +0 and -0. JavaScript has two zeros, a positive zero and a negative zero, because the sign and the magnitude of a number are stored separately. In most of this book, I pretend that there is only a single zero, and you almost never see in JavaScript that there are two of them.

NaN

The error value NaN (an abbreviation for “not a number”) is, ironically, a number value:

> typeof NaN
'number'

It is produced by errors such as the following:

A number could not be parsed:

> Number('xyz')
NaN
> Number(undefined)
NaN

An operation failed:

> Math.acos(2)
NaN
> Math.log(-1)
NaN
> Math.sqrt(-1)
NaN

One of the operands is NaN (this ensures that, if an error occurs during a longer computation, you can see it in the final result):
```
> NaN + 3
NaN
> 25 / NaN
NaN
```

Pitfall: checking whether a value is NaN

NaN is the only value that is not equal to itself:

> NaN === NaN
false

Strict equality (===) is also used by Array.prototype.indexOf. You therefore can’t search for NaN in an array via that method:

> [ NaN ].indexOf(NaN)
-1

If you want to check whether a value is NaN, you have to use the global function isNaN():

> isNaN(NaN)
true
> isNaN(33)
false

However, isNaN does not work properly with nonnumbers, because it first converts those to numbers. That conversion can produce NaN and then the function incorrectly returns true:

> isNaN('xyz')
true

Thus, it is best to combine isNaN with a type check:

function myIsNaN(value) {
    return typeof value === 'number' && isNaN(value);
}

Alternatively, you can check whether the value is unequal to itself (as NaN is the only value with this trait). But that is less self-explanatory:

function myIsNaN(value) {
    return value !== value;
}

Note that this behavior is dictated by IEEE 754. As noted in Section 7.11, “Details of comparison predicates”:^[15]

Every NaN shall compare unordered with everything, including itself.

Infinity

Infinity is an error value indicating one of two problems: a number can’t be represented because its magnitude is too large, or a division by zero has happened.

Infinity is larger than any other number (except NaN). Similarly, -Infinity is smaller than any other number (except NaN). That makes them useful as default values—for example, when you are looking for a minimum or maximum.

Error: a number’s magnitude is too large

How large a number’s magnitude can become is determined by its internal representation (as discussed in The Internal Representation of Numbers), which is the arithmetic product of:

A mantissa (a binary number 1.f₁f₂...)
2 to the power of an exponent

The exponent must be between (and excluding) −1023 and 1024. If the exponent is too small, the number becomes 0. If the exponent is too large, it becomes Infinity. 2¹⁰²³ can still be represented, but 2¹⁰²⁴ can’t:

> Math.pow(2, 1023)
8.98846567431158e+307
> Math.pow(2, 1024)
Infinity

Error: division by zero

Dividing by zero produces Infinity as an error value:

> 3 / 0
Infinity
> 3 / -0
-Infinity

Computing with Infinity

You get the error result NaN if you try to “neutralize” one Infinity with another one:

> Infinity - Infinity
NaN
> Infinity / Infinity
NaN

If you try to go beyond Infinity, you still get Infinity:

> Infinity + Infinity
Infinity
> Infinity * Infinity
Infinity

Checking for Infinity

Strict and lenient equality work fine for Infinity:

> var x = Infinity;
> x === Infinity
true

Additionally, the global function isFinite() allows you to check whether a value is an actual number (neither infinite nor NaN):

> isFinite(5)
true
> isFinite(Infinity)
false
> isFinite(NaN)
false

Two Zeros

Because JavaScript’s numbers keep magnitude and sign separate, each nonnegative number has a negative, including 0.

The rationale for this is that whenever you represent a number digitally, it can become so small that it is indistinguishable from 0, because the encoding is not precise enough to represent the difference. Then a signed zero allows you to record “from which direction” you approached zero; that is, what sign the number had before it was considered zero. Wikipedia nicely sums up the pros and cons of signed zeros:

It is claimed that the inclusion of signed zero in IEEE 754 makes it much easier to achieve numerical accuracy in some critical problems, in particular when computing with complex elementary functions. On the other hand, the concept of signed zero runs contrary to the general assumption made in most mathematical fields (and in most mathematics courses) that negative zero is the same thing as zero. Representations that allow negative zero can be a source of errors in programs, as software developers do not realize (or may forget) that, while the two zero representations behave as equal under numeric comparisons, they are different bit patterns and yield different results in some operations.

Best practice: pretend there’s only one zero

JavaScript goes to great lengths to hide the fact that there are two zeros. Given that it normally doesn’t matter that they are different, it is recommended that you play along with the illusion of the single zero. Let’s examine how that illusion is maintained.

In JavaScript, you normally write 0, which means +0. But -0 is also displayed as simply 0. This is what you see when you use a browser command line or the Node.js REPL:

> -0
0

That is because the standard toString() method converts both zeros to the same '0':

> (-0).toString()
'0'
> (+0).toString()
'0'

Equality doesn’t distinguish zeros, either. Not even ===:

> +0 === -0
true

Array.prototype.indexOf uses === to search for elements, maintaining the illusion:

> [ -0, +0 ].indexOf(+0)
0
> [ +0, -0 ].indexOf(-0)
0

The ordering operators also consider the zeros to be equal:

> -0 < +0
false
> +0 < -0
false

Distinguishing the two zeros

How can you actually observe that the two zeros are different? You can divide by zero (-Infinity and +Infinity can be distinguished by ===):

> 3 / -0
-Infinity
> 3 / +0
Infinity

Another way to perform the division by zero is via Math.pow() (see Numerical Functions):

> Math.pow(-0, -1)
-Infinity
> Math.pow(+0, -1)
Infinity

Math.atan2() (see Trigonometric Functions) also reveals that the zeros are different:

> Math.atan2(-0, -1)
-3.141592653589793
> Math.atan2(+0, -1)
3.141592653589793

The canonical way of telling the two zeros apart is the division by zero. Therefore, a function for detecting negative zeros would look like this:

function isNegativeZero(x) {
    return x === 0 && (1/x < 0);
}

Here is the function in use:

> isNegativeZero(0)
false
> isNegativeZero(-0)
true
> isNegativeZero(33)
false

The Internal Representation of Numbers

JavaScript numbers have 64-bit precision, which is also called double precision (type double in some programming languages). The internal representation is based on the IEEE 754 standard. The 64 bits are distributed between a number’s sign, exponent, and fraction as follows:

Sign	Exponent ∈ [−1023, 1024]	Fraction
1 bit	11 bits	52 bits
Bit 63	Bits 62–52	Bits 51–0

The value of a number is computed by the following formula:

(–1)^sign × %1.fraction × 2^exponent

The prefixed percentage sign (%) means that the number in the middle is written in binary notation: a 1, followed by a binary point, followed by a binary fraction—namely the binary digits of the fraction (a natural number). Here are some examples of this representation:

+0		(sign = 0, fraction = 0, exponent = −1023)
–0		(sign = 1, fraction = 0, exponent = −1023)
1	= (−1)⁰ × %1.0 × 2⁰	(sign = 0, fraction = 0, exponent = 0)
2	= (−1)⁰ × %1.0 × 2¹
3	= (−1)⁰ × %1.1 × 2¹	(sign = 0, fraction = 2⁵¹, exponent = 0)
0.5	= (−1)⁰ × %1.0 × 2⁻¹
−1	= (−1)¹ × %1.0 × 2⁰

The encodings of +0, −0, and 3 can be explained as follows:

±0: Given that the fraction is always prefixed by a 1, it’s impossible to represent 0 with it. Hence, JavaScript encodes a zero via the fraction 0 and the special exponent −1023. The sign can be either positive or negative, meaning that JavaScript has two zeros (see Two Zeros).
3: Bit 51 is the most significant (highest) bit of the fraction. That bit is 1.

Special Exponents

The previously mentioned representation of numbers is called normalized. In that case, the exponent e is in the range −1023 < e < 1024 (excluding lower and upper bounds). −1023 and 1024 are special exponents:

1024 is used for error values such as NaN and Infinity.
−1023 is used for:
- Zero (if the fraction is 0, as just explained)
- Small numbers close to zero (if the fraction is not 0).
To enable both applications, a different, so-called denormalized, representation is used:
(–1)^sign × %0.fraction × 2^–1022
To compare, the smallest (as in “closest to zero”) numbers in normalized representation are:
(–1)^sign × %1.fraction × 2^–1022
Denormalized numbers are smaller, because there is no leading digit 1.

Handling Rounding Errors

JavaScript’s numbers are usually entered as decimal floating-point numbers, but they are internally represented as binary floating-point numbers. That leads to imprecision. To understand why, let’s forget JavaScript’s internal storage format and take a general look at what fractions can be well represented by decimal floating-point numbers and by binary floating-point numbers. In the decimal system, all fractions are a mantissa m divided by a power of 10:

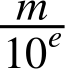
So, in the denominator, there are only tens. That’s why cannot be expressed precisely as a decimal floating-point number—there is no way to get a 3 into the denominator. Binary floating-point numbers only have twos in the denominator. Let’s examine which decimal floating-point numbers can be represented well as binary and which can’t. If there are only twos in the denominator, the decimal number can be represented:

0.5_dec = 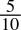= = 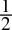0.1_bin
0.75_dec = 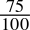= = 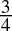0.11_bin
0.125_dec = 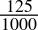= = 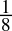0.001_bin

Other fractions cannot be represented precisely, because they have numbers other than 2 in the denominator (after prime factorization):

0.1_dec = =
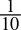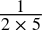
0.2_dec = =

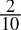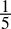
You can’t normally see that JavaScript doesn’t store exactly 0.1 internally. But you can make it visible by multiplying it with a high enough power of 10:

> 0.1 * Math.pow(10, 24)
1.0000000000000001e+23

And if you add two imprecisely represented numbers, the result is sometimes imprecise enough that the imprecision becomes visible:

> 0.1 + 0.2
0.30000000000000004

Another example:

> 0.1 + 1 - 1
0.10000000000000009

Due to rounding errors, as a best practice you should not compare nonintegers directly. Instead, take an upper bound for rounding errors into consideration. Such an upper bound is called a machine epsilon. The standard epsilon value for double precision is 2⁻⁵³:

var EPSILON = Math.pow(2, -53);
function epsEqu(x, y) {
    return Math.abs(x - y) < EPSILON;
}

epsEqu() ensures correct results where a normal comparison would be inadequate:

> 0.1 + 0.2 === 0.3
false
> epsEqu(0.1+0.2, 0.3)
true

Integers in JavaScript

As mentioned before, JavaScript has only floating-point numbers. Integers appear internally in two ways. First, most JavaScript engines store a small enough number without a decimal fraction as an integer (with, for example, 31 bits) and maintain that representation as long as possible. They have to switch back to a floating-point representation if a number’s magnitude grows too large or if a decimal fraction appears.

Second, the ECMAScript specification has integer operators: namely, all of the bitwise operators. Those operators convert their operands to 32-bit integers and return 32-bit integers. For the specification, integer only means that the numbers don’t have a decimal fraction, and 32-bit means that they are within a certain range. For engines, 32-bit integer means that an actual integer (non-floating-point) representation can usually be introduced or maintained.

Ranges of Integers

Internally, the following ranges of integers are important in JavaScript:

Safe integers (see Safe Integers), the largest practically usable range of integers that JavaScript supports:
- 53 bits plus a sign, range (−2⁵³, 2⁵³)
Array indices (see Array Indices):
- 32 bits, unsigned
- Maximum length: 2³²−1
- Range of indices: [0, 2³²−1) (excluding the maximum length!)
Bitwise operands (see Bitwise Operators):
- Unsigned right shift operator (>>>): 32 bits, unsigned, range [0, 2³²)
- All other bitwise operators: 32 bits, including a sign, range [−2³¹, 2³¹)
“Char codes,” UTF-16 code units as numbers:
- Accepted by String.fromCharCode() (see String Constructor Method)
- Returned by String.prototype.charCodeAt() (see Extract Substrings)
- 16 bits, unsigned

Representing Integers as Floating-Point Numbers

JavaScript can only handle integer values up to a magnitude of 53 bits (the 52 bits of the fraction plus 1 indirect bit, via the exponent; see The Internal Representation of Numbers for details).

The following table explains how JavaScript represents 53-bit integers as floating-point numbers:

Bits	Range	Encoding
1 bit	0	(See The Internal Representation of Numbers.)
1 bit	1	%1 × 2⁰
2 bits	2–3	%1.f₅₁ × 2¹
3 bits	4–7 = 2²–(2³−1)	%1.f₅₁f₅₀ × 2²
4 bits	2³–(2⁴−1)	%1.f₅₁f₅₀f₄₉ × 2³
⋯	⋯	⋯
53 bits	2⁵²–(2⁵³−1)	%1.f₅₁⋯f₀ × 2⁵²

There is no fixed sequence of bits that represents the integer. Instead, the mantissa %1.f is shifted by the exponent, so that the leading digit 1 is in the right place. In a way, the exponent counts the number of digits of the fraction that are in active use (the remaining digits are 0). That means that for 2 bits, we use one digit of the fraction and for 53 bits, we use all digits of the fraction. Additionally, we can represent 2⁵³ as %1.0 × 2⁵³, but we get problems with higher numbers:

Bits	Range	Encoding
54 bits	2⁵³–(2⁵⁴−1)	%1.f₅₁⋯f₀0 × 2⁵³
55 bits	2⁵⁴–(2⁵⁵−1)	%1.f₅₁⋯f₀00 × 2⁵⁴
⋯

For 54 bits, the least significant digit is always 0, for 55 bits the two least significant digits are always 0, and so on. That means that for 54 bits, we can only represent every second number, for 55 bits only every fourth number, and so on. For example:

> Math.pow(2, 53) - 1  // OK
9007199254740991
> Math.pow(2, 53)  // OK
9007199254740992
> Math.pow(2, 53) + 1  // can't be represented
9007199254740992
> Math.pow(2, 53) + 2  // OK
9007199254740994

Best practice

If you work with integers of up to 53 bits magnitude, you are fine. Unfortunately, you’ll often encounter 64-bit unsigned integers in programming (Twitter IDs, databases, etc.). These must be stored in strings in JavaScript. If you want to perform arithmetic with such integers, you need special libraries. There are plans to bring larger integers to JavaScript, but that will take a while.

Safe Integers

JavaScript can only safely represent integers i in the range −2⁵³ < i < 2⁵³. This section examines what that means and what the consequences are. It is based on an email by Mark S. Miller to the es-discuss mailing list.

The idea of a safe integer centers on how mathematical integers are represented in JavaScript. In the range (−2⁵³, 2⁵³) (excluding the lower and upper bounds), JavaScript integers are safe: there is a one-to-one mapping between mathematical integers and their representations in JavaScript.

Beyond this range, JavaScript integers are unsafe: two or more mathematical integers are represented as the same JavaScript integer. For example, starting at 2⁵³, JavaScript can represent only every second mathematical integer (the previous section explains why). Therefore, a safe JavaScript integer is one that unambiguously represents a single mathematical integer.

Definitions in ECMAScript 6

ECMAScript 6 will provide the following constants:

Number.MAX_SAFE_INTEGER = Math.pow(2, 53)-1;
Number.MIN_SAFE_INTEGER = -Number.MAX_SAFE_INTEGER;

It will also provide a function for determining whether an integer is safe:

Number.isSafeInteger = function (n) {
    return (typeof n === 'number' &&
        Math.round(n) === n &&
        Number.MIN_SAFE_INTEGER <= n &&
        n <= Number.MAX_SAFE_INTEGER);
}

For a given value n, this function first checks whether n is a number and an integer. If both checks succeed, n is safe if it is greater than or equal to MIN_SAFE_INTEGER and less than or equal to MAX_SAFE_INTEGER.

Safe results of arithmetic computations

How can we make sure that results of arithmetic computations are correct? For example, the following result is clearly not correct:

> 9007199254740990 + 3
9007199254740992

We have two safe operands, but an unsafe result:

> Number.isSafeInteger(9007199254740990)
true
> Number.isSafeInteger(3)
true
> Number.isSafeInteger(9007199254740992)
false

The following result is also incorrect:

> 9007199254740995 - 10
9007199254740986

This time, the result is safe, but one of the operands isn’t:

> Number.isSafeInteger(9007199254740995)
false
> Number.isSafeInteger(10)
true
> Number.isSafeInteger(9007199254740986)
true

Therefore, the result of applying an integer operator op is guaranteed to be correct only if all operands and the result are safe. More formally:

isSafeInteger(a) && isSafeInteger(b) && isSafeInteger(a op b)

implies that a op b is a correct result.

Converting to Integer

In JavaScript, all numbers are floating point. Integers are floating-point numbers without a fraction. Converting a number n to an integer means finding the integer that is “closest” to n (where the meaning of “closest” depends on how you convert). You have several options for performing this conversion:

The Math functions Math.floor(), Math.ceil(), and Math.round() (see Integers via Math.floor(), Math.ceil(), and Math.round())
The custom function ToInteger() (see Integers via the Custom Function ToInteger())
Binary bitwise operators (see 32-bit Integers via Bitwise Operators)
The global function parseInt() (see Integers via parseInt())

Spoiler: #1 is usually the best choice, #2 and #3 have niche applications, and #4 is OK for parsing strings, but not for converting numbers to integers.

Integers via Math.floor(), Math.ceil(), and Math.round()

The following three functions are usually the best way of converting a number to an integer:

Math.floor() converts its argument to the closest lower integer:
```
> Math.floor(3.8)
3
> Math.floor(-3.8)
-4
```
Math.ceil() converts its argument to the closest higher integer:
```
> Math.ceil(3.2)
4
> Math.ceil(-3.2)
-3
```

Math.round() converts its argument to the closest integer:

> Math.round(3.2)
3
> Math.round(3.5)
4
> Math.round(3.8)
4

The result of rounding -3.5 may be surprising:

> Math.round(-3.2)
-3
> Math.round(-3.5)
-3
> Math.round(-3.8)
-4

Therefore, Math.round(x) is the same as:

Math.floor(x + 0.5)

Integers via the Custom Function ToInteger()

Another good option for converting any value to an integer is the internal ECMAScript operation ToInteger(), which removes the fraction of a floating-point number. If it was accessible in JavaScript, it would work like this:

> ToInteger(3.2)
3
> ToInteger(3.5)
3
> ToInteger(3.8)
3
> ToInteger(-3.2)
-3
> ToInteger(-3.5)
-3
> ToInteger(-3.8)
-3

The ECMAScript specification defines the result of ToInteger(number) as:

sign(number) × floor(abs(number))

For what it does, this formula is relatively complicated because floor seeks the closest larger integer; if you want to remove the fraction of a negative integer, you have to seek the closest smaller integer. The following code implements the operation in JavaScript. We avoid the sign operation by using ceil if the number is negative:

function ToInteger(x) {
    x = Number(x);
    return x < 0 ? Math.ceil(x) : Math.floor(x);
}

32-bit Integers via Bitwise Operators

Binary bitwise operators (see Binary Bitwise Operators) convert (at least) one of their operands to a 32-bit integer that is then manipulated to produce a result that is also a 32-bit integer. Therefore, if you choose the other operand appropriately, you get a fast way to convert an arbitrary number to a 32-bit integer (that is either signed or unsigned).

Bitwise Or (|)

If the mask, the second operand, is 0, you don’t change any bits and the result is the first operand, coerced to a signed 32-bit integer. This is the canonical way to execute this kind of coercion and is used, for example, by asm.js (refer back to Is JavaScript Fast Enough?):

// Convert x to a signed 32-bit integer
function ToInt32(x) {
    return x | 0;
}

ToInt32() removes the fraction and applies modulo 2³²:

> ToInt32(1.001)
1
> ToInt32(1.999)
1
> ToInt32(1)
1
> ToInt32(-1)
-1
> ToInt32(Math.pow(2, 32)+1)
1
> ToInt32(Math.pow(2, 32)-1)
-1

Shift operators

The same trick that worked for bitwise Or also works for shift operators: if you shift by zero bits, the result of a shift operation is the first operand, coerced to a 32-bit integer. Here are some examples of implementing operations of the ECMAScript specification via shift operators:

// Convert x to a signed 32-bit integer
function ToInt32(x) {
    return x << 0;
}

// Convert x to a signed 32-bit integer
function ToInt32(x) {
    return x >> 0;
}

// Convert x to an unsigned 32-bit integer
function ToUint32(x) {
    return x >>> 0;
}

Here is ToUint32() in action:

> ToUint32(-1)
4294967295
> ToUint32(Math.pow(2, 32)-1)
4294967295
> ToUint32(Math.pow(2, 32))
0

Should I use bitwise operators to coerce to integer?

You have to decide for yourself if the slight increase in efficiency is worth your code being harder to understand. Also note that bitwise operators artificially limit themselves to 32 bits, which is often neither necessary nor useful. Using one of the Math functions, possibly in addition to Math.abs(), is a more self-explanatory and arguably better choice.

Integers via parseInt()

The parseInt() function:

parseInt(str, radix?)

parses the string str (nonstrings are coerced) as an integer. The function ignores leading whitespace and considers as many consecutive legal digits as it can find.

The radix

The range of the radix is 2 ≤ radix ≤ 36. It determines the base of the number to be parsed. If the radix is greater than 10, letters are used as digits (case-insensitively), in addition to 0–9.

If radix is missing, then it is assumed to be 10, except if str begins with “0x” or “0X,” in which case radix is set to 16 (hexadecimal):

> parseInt('0xA')
10

If radix is already 16, then the hexadecimal prefix is optional:

> parseInt('0xA', 16)
10
> parseInt('A', 16)
10

So far I have described the behavior of parseInt() according to the ECMAScript specification. Additionally, some engines set the radix to 8 if str starts with a zero:

> parseInt('010')
8
> parseInt('0109')  // ignores digits ≥ 8
8

Thus, it is best to always explicitly state the radix, to always call parseInt() with two arguments.

Here are a few examples:

> parseInt('')
NaN
> parseInt('zz', 36)
1295
> parseInt('   81', 10)
81

> parseInt('12**', 10)
12
> parseInt('12.34', 10)
12
> parseInt(12.34, 10)
12

Don’t use parseInt() to convert a number to an integer. The last example gives us hope that we might be able to use parseInt() for converting numbers to integers. Alas, here is an example where the conversion is incorrect:

> parseInt(1000000000000000000000.5, 10)
1

Explanation

The argument is first converted to a string:

> String(1000000000000000000000.5)
'1e+21'

parseInt doesn’t consider “e” to be an integer digit and thus stops parsing after the 1. Here’s another example:

> parseInt(0.0000008, 10)
8
> String(0.0000008)
'8e-7'

Summary

parseInt() shouldn’t be used to convert numbers to integers: coercion to string is an unnecessary detour and even then, the result is not always correct.

parseInt() is useful for parsing strings, but you have to be aware that it stops at the first illegal digit. Parsing strings via Number() (see The Function Number) is less forgiving, but may produce nonintegers.

Arithmetic Operators

The following operators are available for numbers:

number1 + number2

Numerical addition, unless either of the operands is a string. Then both operands are converted to strings and concatenated (see The Plus Operator (+)):

> 3.1 + 4.3
7.4
> 4 + ' messages'
'4 messages'

number1 - number2

Subtraction.

number1 * number2

Multiplication.

number1 / number2

Division.

number1 % number2

Remainder:

> 9 % 7
2
> -9 % 7
-2

Warning

This operation is not modulo. It returns a value whose sign is the same as the first operand (more details in a moment).

-number

Negates its operand.

+number

Leaves its operand as is; nonnumbers are converted to a number.

++variable, --variable

Returns the current value of the variable after incrementing (or decrementing) it by 1:

> var x = 3;
> ++x
4
> x
4

variable++, variable--

Increments (or decrements) the value of the variable by 1 and returns it:

> var x = 3;
> x++
3
> x
4

Mnemonic: increment (++) and decrement (--) operators

The position of the operand can help you remember whether it is returned before or after incrementing (or decrementing) it. If the operand comes before the increment operator, it is returned before incrementing it. If the operand comes after the operator, it is incremented and then returned. (The decrement operator works similarly.)

The result of the remainder operator always has the sign of the first operand (for modulo, it is the sign of the second operand):

> -5 % 2
-1

That means that the following function does not work:

// Wrong!
function isOdd(n) {
    return n % 2 === 1;
}
console.log(isOdd(-5)); // false
console.log(isOdd(-4)); // false

The correct version is:

function isOdd(n) {
    return Math.abs(n % 2) === 1;
}
console.log(isOdd(-5)); // true
console.log(isOdd(-4)); // false

Bitwise Operators

JavaScript has several bitwise operators that work with 32-bit integers. That is, they convert their operands to 32-bit integers and produce a result that is a 32-bit integer. Use cases for these operators include processing binary protocols, special algorithms, etc.

Background Knowledge

This section explains a few concepts that will help you understand bitwise operators.

Binary complements

Two common ways of computing a binary complement (or inverse) of a binary number are:

Ones’ complement

You compute the ones’ complement ~x of a number x by inverting each of the 32 digits. Let’s illustrate the ones’ complement via four-digit numbers. The ones’ complement of 1100 is 0011. Adding a number to its ones’ complement results in a number whose digits are all 1:

1 + ~1 = 0001 + 1110 = 1111

Twos’ complement

The twos’ complement -x of a number x is the ones’ complement plus one. Adding a number to its twos’ complement results in 0 (ignoring overflow beyond the most significant digit). Here’s an example using four-digit numbers:

1 + -1 = 0001 + 1111 = 0000

Signed 32-bit integers

32-bit integers don’t have an explicit sign, but you can still encode negative numbers. For example, −1 can be encoded as the twos’ complement of 1: adding 1 to the result yields 0 (within 32 bits). The boundary between positive and negative numbers is fluid; 4294967295 (2³²−1) and −1 are the same integer here. But you have to decide on a sign when you convert such an integer from or to a JavaScript number, which has an explicit sign as opposed to an implicit one. Therefore, signed 32-bit integers are partitioned into two groups:

Highest bit is 0: number is zero or positive.
Highest bit is 1: number is negative.

The highest bit is often called the sign bit. Accordingly, 4294967295, interpreted as a signed 32-bit integer, becomes −1 when converted to a JavaScript number:

> ToInt32(4294967295)
-1

ToInt32() is explained in 32-bit Integers via Bitwise Operators.

Note

Only the unsigned right shift operator (>>>) works with unsigned 32-bit integers; all other bitwise operators work with signed 32-bit integers.

Inputting and outputting binary numbers

In the following examples, we work with binary numbers via the following two operations:

parseInt(str, 2) (see Integers via parseInt()) parses a string str in binary notation (base 2). For example:
```
> parseInt('110', 2)
6
```
num.toString(2) (see Number.prototype.toString(radix?)) converts the number num to a string in binary notation. For example:
```
> 6..toString(2)
'110'
```

Bitwise Not Operator

~number computes the ones’ complement of number:

> (~parseInt('11111111111111111111111111111111', 2)).toString(2)
'0'

Binary Bitwise Operators

JavaScript has three binary bitwise operators:

number1 & number2 (bitwise And):

> (parseInt('11001010', 2) & parseInt('1111', 2)).toString(2)
'1010'

number1 | number2 (bitwise Or):

> (parseInt('11001010', 2) | parseInt('1111', 2)).toString(2)
'11001111'

number1 ^ number2 (bitwise Xor; eXclusive Or):

> (parseInt('11001010', 2) ^ parseInt('1111', 2)).toString(2)
'11000101'

There are two ways to intuitively understand binary bitwise operators:

One boolean operation per bit

In the following formulas, n_i means bit i of number n interpreted as a boolean (0 is false, 1 is true). For example, 2₀ is false; 2₁ is true:

And: result_i = number1_i && number2_i
Or: result_i = number1_i || number2_i
Xor: result_i = number1_i ^^ number2_i
The operator ^^ does not exist. If it did, it would work like this (the result is true if exactly one of the operands is true):
```
x ^^ y === (x && !y) || (!x && y)
```

Changing bits of number1 via number2

And: Keeps only those bits of number1 that are set in number2. This operation is also called masking, with number2 being the mask.
Or: Sets all bits of number1 that are set in number2 and keeps all other bits unchanged.
Xor: Inverts all bits of number1 that are set in number2 and keeps all other bits unchanged.

Bitwise Shift Operators

JavaScript has three bitwise shift operators:

number << digitCount (left shift):

> (parseInt('1', 2) << 1).toString(2)
'10'

number >> digitCount (signed right shift):
The 32-bit binary number is interpreted as signed (see the preceding section). When shifting right, the sign is preserved:
```
> (parseInt('11111111111111111111111111111110', 2) >> 1).toString(2)
'-1'
```
We have right-shifted –2. The result, –1, is equivalent to a 32-bit integer whose digits are all 1 (the twos’ complement of 1). In other words, a signed right shift by one digit divides both negative and positive integers by two.
number >>> digitCount` (unsigned right shift):
```
> (parseInt('11100', 2) >>> 1).toString(2)
'1110'
```
As you can see, this operator shifts in zeros from the left.

The Function Number

The function Number can be invoked in two ways:

Number(value)

As a normal function, it converts value to a primitive number (see Converting to Number):

> Number('123')
123
> typeof Number(3)  // no change
'number'

new Number(num)

As a constructor, it creates a new instance of Number (see Wrapper Objects for Primitives), an object that wraps num (after converting it to a number). For example:

> typeof new Number(3)
'object'

The former invocation is the common one.

Number Constructor Properties

The object Number has the following properties:

Number.MAX_VALUE

The largest positive number that can be represented. Internally, all digits of its fraction are ones and the exponent is maximal, at 1023. If you try to increment the exponent by multiplying it by two, the result is the error value Infinity (see Infinity):

> Number.MAX_VALUE
1.7976931348623157e+308
> Number.MAX_VALUE * 2
Infinity

Number.MIN_VALUE

The smallest representable positive number (greater than zero, a tiny fraction):

> Number.MIN_VALUE
5e-324

Number.NaN

The same value as the global NaN.

Number.NEGATIVE_INFINITY

The same value as -Infinity:

> Number.NEGATIVE_INFINITY === -Infinity
true

Number.POSITIVE_INFINITY

The same value as Infinity:

> Number.POSITIVE_INFINITY === Infinity
true

Number Prototype Methods

All methods of primitive numbers are stored in Number.prototype (see Primitives Borrow Their Methods from Wrappers).

Number.prototype.toFixed(fractionDigits?)

Number.prototype.toFixed(fractionDigits?) returns an exponent-free representation of the number, rounded to fractionDigits digits. If the parameter is omitted, the value 0 is used:

> 0.0000003.toFixed(10)
'0.0000003000'
> 0.0000003.toString()
'3e-7'

If the number is greater than or equal to 10²¹, then this method works the same as toString(). You get a number in exponential notation:

> 1234567890123456789012..toFixed()
'1.2345678901234568e+21'
> 1234567890123456789012..toString()
'1.2345678901234568e+21'

Number.prototype.toPrecision(precision?)

Number.prototype.toPrecision(precision?) prunes the mantissa to precision digits before using a conversion algorithm similar to toString(). If no precision is given, toString() is used directly:

> 1234..toPrecision(3)
'1.23e+3'

> 1234..toPrecision(4)
'1234'

> 1234..toPrecision(5)
'1234.0'

> 1.234.toPrecision(3)
'1.23'

You need the exponential notation to display 1234 with a precision of three digits.

Number.prototype.toString(radix?)

For Number.prototype.toString(radix?), the parameter radix indicates the base of the system in which the number is to be displayed. The most common radices are 10 (decimal), 2 (binary), and 16 (hexadecimal):

> 15..toString(2)
'1111'
> 65535..toString(16)
'ffff'

The radix must be at least 2 and at most 36. Any radix greater than 10 leads to alphabetical characters being used as digits, which explains the maximum 36, as the Latin alphabet has 26 characters:

> 1234567890..toString(36)
'kf12oi'

The global function parseInt (see Integers via parseInt()) allows you to convert such notations back to a number:

> parseInt('kf12oi', 36)
1234567890

Decimal exponential notation

For the radix 10, toString() uses exponential notation (with a single digit before the decimal point) in two cases. First, if there are more than 21 digits before the decimal point of a number:

> 1234567890123456789012
1.2345678901234568e+21
> 123456789012345678901
123456789012345680000

Second, if a number starts with 0. followed by more than five zeros and a non-zero digit:

> 0.0000003
3e-7
> 0.000003
0.000003

In all other cases, a fixed notation is used.

Number.prototype.toExponential(fractionDigits?)

Number.prototype.toExponential(fractionDigits?) forces a number to be expressed in exponential notation. fractionDigits is a number between 0 and 20 that determines how many digits should be shown after the decimal point. If it is omitted, then as many significant digits are included as necessary to uniquely specify the number.

In this example, we force more precision when toString() would also use exponential notation. Results are mixed, because we reach the limits of the precision that can be achieved when converting binary numbers to a decimal notation:

> 1234567890123456789012..toString()
'1.2345678901234568e+21'

> 1234567890123456789012..toExponential(20)
'1.23456789012345677414e+21'

In this example, the magnitude of the number is not large enough for an exponent being displayed by toString(). However, toExponential() does display an exponent:

> 1234..toString()
'1234'

> 1234..toExponential(5)
'1.23400e+3'

> 1234..toExponential()
'1.234e+3'

In this example, we get exponential notation when the fraction is not small enough:

> 0.003.toString()
'0.003'

> 0.003.toExponential(4)
'3.0000e-3'

> 0.003.toExponential()
'3e-3'

Functions for Numbers

The following functions operate on numbers:

isFinite(number): Checks whether number is an actual number (neither Infinity nor NaN). For details, see Checking for Infinity.
isNaN(number): Returns true if number is NaN. For details, see Pitfall: checking whether a value is NaN.
parseFloat(str): Turns str into a floating-point number. For details, see parseFloat().
parseInt(str, radix?): Parses str as an integer whose base is radix (2–36). For details, see Integers via parseInt().

Sources for This Chapter

I referred to the following sources while writing this chapter:

“IEEE Standard 754 Floating Point Numbers” by Steve Hollasch
“Data Types and Scaling (Fixed-Point Blockset)” in the MATLAB documentation
“IEEE floating point” on Wikipedia

^[14]Source: Brendan Eich, http://bit.ly/1lKzQeC.

^[15]Béla Varga (@netzzwerg) pointed out that IEEE 754 specifies NaN as not equal to itself.

Get Speaking JavaScript now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial