SQL and Relational Theory, 2nd Edition

GROUP, UNGROUP, AND RELATION VALUED ATTRIBUTES

Recall from Chapter 2 that relations with relation valued attributes (RVAs for short) are legal. Figure 7-1 below shows relations R1 and R4 from Figure 2-1 and Figure 2-2 in that chapter; R4 has an RVA and R1 doesn’t, but the two relations clearly represent the same information.

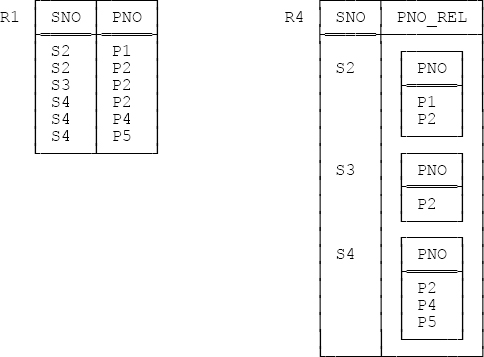
Figure 7-1. Relations R1 and R4 from Figure 2-1 and Figure 2-2 in Chapter 2

Now, we obviously need a way to map between relations without RVAs and relations with them, and that’s the purpose of the GROUP and UNGROUP operators. I don’t want to go into a lot of detail on those operators here; let me just say that, given the relations shown in Figure 7-1, the expression

     R1 GROUP ( { PNO } AS PNO_REL )

will produce R4, and the expression

     R4 UNGROUP ( PNO_REL )

will produce R1.

By the way, it’s worth noting that the following expression—

     EXTEND R1 { SNO } : { PNO_REL := !!R1 }

—will produce exactly the same result as the GROUP example shown above. In other words, GROUP can be defined in terms of EXTEND and image relations. Now, I’m not suggesting that we get rid of our useful GROUP operator; quite apart from anything else, a language that had an explicit UNGROUP operator (as Tutorial D does) but no explicit GROUP operator could certainly be criticized on ergonomic grounds, if nothing else. But it’s at least interesting, and perhaps pedagogically helpful, to note that the ...