Statistical and Machine Learning Approaches for Network Analysis

2.6 Clustered Network

2.6.1 Clustering Coefficient

Highly connected subnetworks are embedded in real-world networks by groups and modules. To measure the clustering effects, the clustering coefficient [18] was proposed. This measure denotes the density among neighbors of node i, and is defined as the ratio of the number of edges among the neighbors to the number of all possible connections among the neighbors:

(2.19)

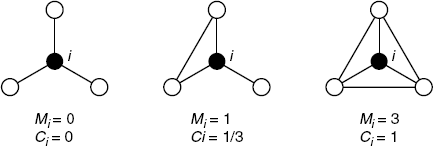
where M_i is the number of edges among the neighbors of node i (see Fig. 2.7). The overall tendency of clustering is measured by the average clustering coefficient . A high average clustering coefficient implies that the network is clustered.

Figure 2.7 The clustering coefficients of node i with degree of 3 (i.e., k_i = 3).

In random networks, since the probability that an edge is drawn between a given node pair is p, the clustering coefficient is equivalent to the probability p (the model parameter) C^rand = p. Assuming that real-world networks are randomly constructed, the clustering coefficient is estimated as

(2.20)

where E and N are the number of edges and nodes, respectively. ...