7.2 The Sampling Distribution of The Mean
Suppose μ is some unknown population mean. We want to determine its “true value.” How should we proceed to find μ? A reasonable approach is to take a simple random sample and make an inference from the sample to the population. How is this inference made? We use an estimator for μ. Think of an estimator as a function of the sample values used to estimate μ. A logical estimator for μ is the sample mean ![]() . (Specifying an estimator is a form of data reduction—we summarize the information about μ contained in a sample by determining some essential characteristic of the sample values. So for purposes of inference about μ, we employ the realization of
. (Specifying an estimator is a form of data reduction—we summarize the information about μ contained in a sample by determining some essential characteristic of the sample values. So for purposes of inference about μ, we employ the realization of ![]() rather than the entire set of observed data points.) Under random sampling,
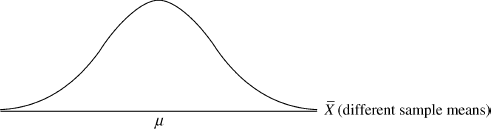
rather than the entire set of observed data points.) Under random sampling, ![]() is a random variable and thus has a probability distribution that we shall term the sampling distribution of the mean—a distribution showing the probabilities of obtaining different sample means from random samples of size n taken from a population of size N (Fig. 7.1).
is a random variable and thus has a probability distribution that we shall term the sampling distribution of the mean—a distribution showing the probabilities of obtaining different sample means from random samples of size n taken from a population of size N (Fig. 7.1).
Figure 7.1 Sampling distribution of the mean.
We shall call ...
Get Statistical Inference: A Short Course now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

