July 2012
Intermediate to advanced
400 pages
9h 33m
English
Content preview from Statistical Inference: A Short Course
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
8.4 A Confidence Interval For The Population Mean μ (σ Unknown)
In the discussion that follows, we shall assume that we are sampling from a normal population. We determined above that a 
confidence interval for the population mean μ is 
when σ is known. But if σ is unknown, it must be estimated by
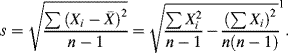
Additionally, if n is “small” 
, then the statistic
follows a t distribution with
degrees of freedom. So once s replaces σ and n is small, the resulting statistic [Eq. (8.10)] is no longer N(0, 1).
Let us examine the properties of the sampling distribution of the t statistic [Eq. (8.10)]:
1. It is symmetrical about a mean of zero and asymptotic to the horizontal axis.
2. There is a different t distribution for each sample size, that is, t varies with 
. This dependency on is termed degrees ...
. This dependency on is termed degrees ...Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.