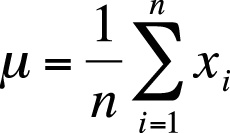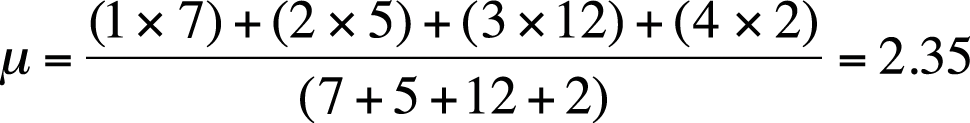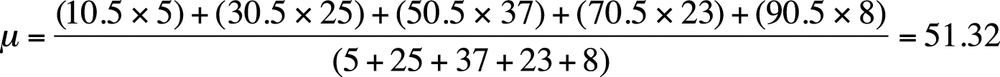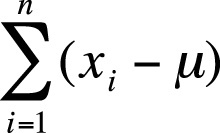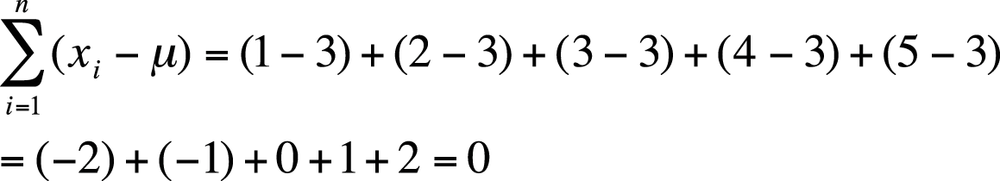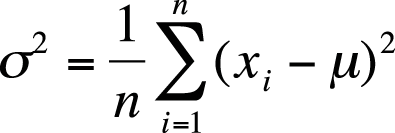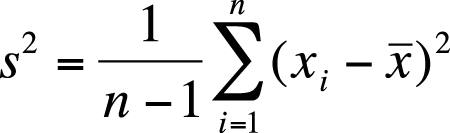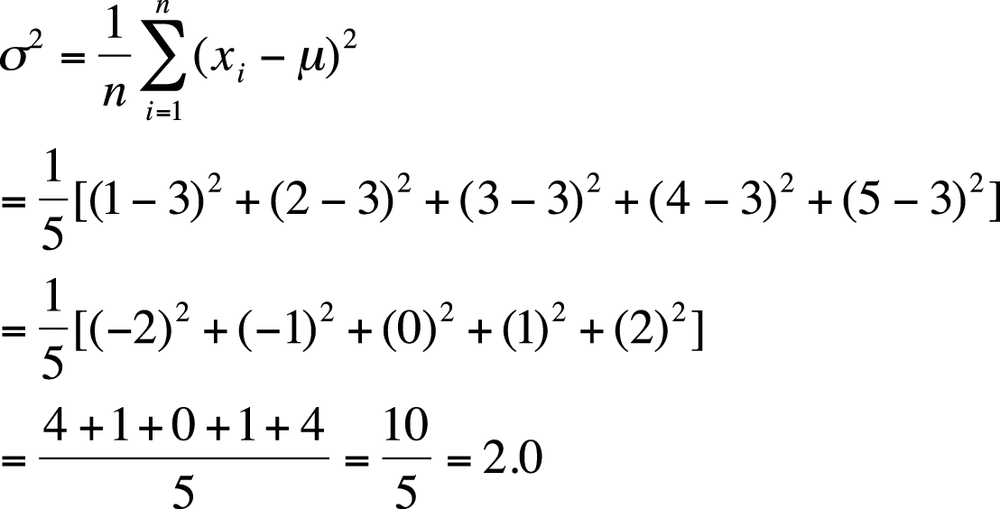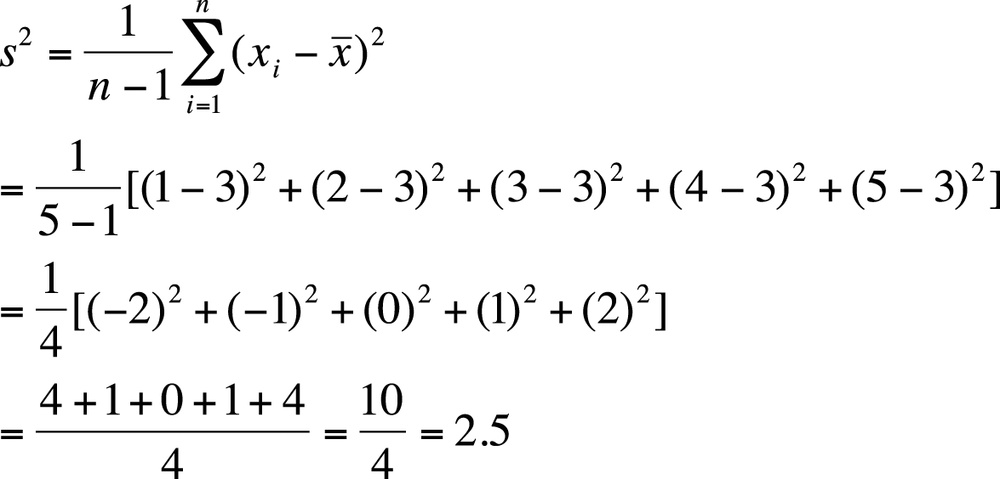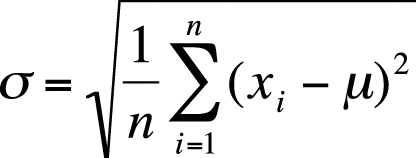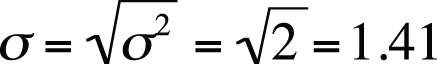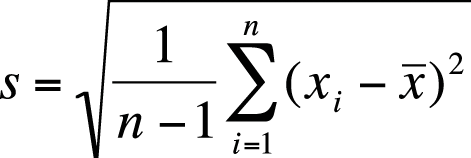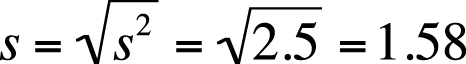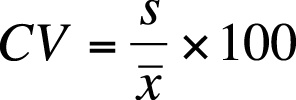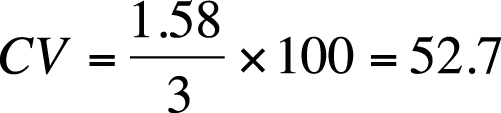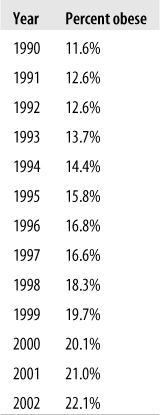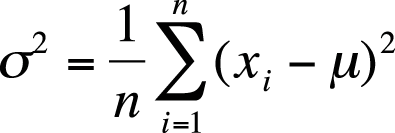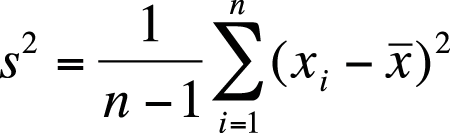Most of this book, as is the case with most statistics books, is concerned with statistical inference, meaning the practice of drawing conclusions about a population by using statistics calculated on a sample. However, another type of statistics is the concern of this chapter: descriptive statistics, meaning the use of statistical and graphic techniques to present information about the data set being studied. Nearly everyone involved in statistical work works with both types of statistics, and often, computing descriptive statistics is a preliminary step in what will ultimately be an inferential statistical analysis. In particular, it is a common practice to begin an analysis by examining graphical displays of a data set and to compute some basic descriptive statistics to get a better sense of the data to be analyzed. You can never be too familiar with your data, and time spent examining it is nearly always time well spent. Descriptive statistics and graphic displays can also be the final product of a statistical analysis. For instance, a business might want to monitor sales volumes for different locations or different sales personnel and wish to present that information using graphics, without any desire to use that information to make inferences (for instance, about other locations or other years) using the data collected.
The same data set may be considered as either a population or a sample, depending on the reason for its collection and analysis. For instance, the final exam grades of the students in a class are a population if the purpose of the analysis is to describe the distribution of scores in that class, but they are a sample if the purpose of the analysis is to make some inference from those scores to the scores of other students (perhaps students in different classes or different schools). Analyzing a population means your data set is the complete population of interest, so you are performing your calculations on all members of the group of interest to you and can make direct statements about the characteristics of that group. In contrast, analyzing a sample means you are working with a subset drawn from a larger population, and any statements made about the larger group from which your sample was drawn are probabilistic rather than absolute. (The reasoning behind inferential statistics is discussed further in Chapter 3.) Samples rather than populations are often analyzed for practical reasons because it might be impossible or prohibitively expensive to study all members of a population directly.
The distinction between descriptive and inferential statistics is fundamental, and a set of notational conventions and terminology has been developed to distinguish between the two. Although these conventions differ somewhat from one author to the next, as a general rule, numbers that describe a population are referred to as parameters and are signified by Greek letters such as µ (for the population mean) and σ (for the population standard deviation); numbers that describe a sample are referred to as statistics and are signified by Latin letters such as ![]() (the sample mean) and s (the sample standard deviation).
(the sample mean) and s (the sample standard deviation).
Measures of central tendency, also known as measures of location, are typically among the first statistics computed for the continuous variables in a new data set. The main purpose of computing measures of central tendency is to give you an idea of what a typical or common value for a given variable is. The three most common measures of central tendency are the arithmetic mean, the median, and the mode.
The arithmetic mean, or simply the mean, is often referred to in ordinary speech as the average of a set of values. Calculating the mean as a measure of central tendency is appropriate for interval and ratio data, and the mean of dichotomous variables coded as 0 or 1 provides the proportion of subjects whose value on the variable is 1. For continuous data, for instance measures of height or scores on an IQ test, the mean is simply calculated by adding up all the values and then dividing by the number of values. The mean of a population is denoted by the Greek letter mu (µ) whereas the mean of a sample is typically denoted by a bar over the variable symbol: for instance, the mean of x would be written ![]() and pronounced “x-bar.” Some authors adapt the bar notation for the names of variables also. For instance, some authors denote “the mean of the variable age” by
and pronounced “x-bar.” Some authors adapt the bar notation for the names of variables also. For instance, some authors denote “the mean of the variable age” by ![]() , which would be pronounced “age-bar.”
, which would be pronounced “age-bar.”
Suppose we have a population with only five cases, and these are the values for members of that population for the variable x:
| 100, 115, 93, 102, 97 |
We can calculate the mean of x by adding these values and dividing by 5 (the number of values):
Statisticians often use a convention called summation notation, introduced in Chapter 1, which defines a statistic by describing how it is calculated. The computation of the mean is the same whether the numbers are considered to represent a population or a sample; the only difference is the symbol for the mean itself. The mean of a population, as expressed in summation notation, is shown in Figure 4-1.
In this formula, µ (the Greek letter mu) is the population mean for x, n is the number of cases (the number of values for x), and xi is the value of x for a particular case. The Greek letter sigma (Σ) means summation (adding together), and the figures above and below the sigma define the range over which the operation should be performed. In this case, the notation says to sum all the values of x from 1 to n. The symbol i designates the position in the data set, so x1 is the first value in the data set, x2 the second value, and xn the last value in the data set. The summation symbol means to add together or sum the values of x from the first (x1) to the last (xn). The population mean is therefore calculated by summing all the values for the variable in question and then dividing by the number of values, remembering that dividing by n is the same thing as multiplying by 1/n.
The mean is an intuitive measure of central tendency that is easy for most people to understand. However, the mean is not an appropriate summary measure for every data set because it is sensitive to extreme values, also known as outliers (discussed further later) and can also be misleading for skewed (nonsymmetrical) data.
Consider one simple example. Suppose the last value in our tiny data set was 297 instead of 97. In this case, the mean would be:
The mean of 141.4 is not a typical value for this data, In fact, 80% of the data (four of the five values) are below the mean, which is distorted by the presence of one extremely high value.
The problem here is not simply theoretical; many large data sets also have a distribution for which the mean is not a good measure of central tendency. This is often true of measures of income, such as household income data in the United States. A few very rich households make the mean household income in the United States a larger value than is truly representative of the average or typical household, and for this reason, the median household income is often reported instead (more about medians later).
The mean can also be calculated using data from a frequency table, that is, a table displaying data values and how often each occurs. Consider the following simple example in Figure 4-2.
To find the mean of these numbers, treat the frequency column as a weighting variable. That is, multiply each value by its frequency. For the denominator, add the frequencies to get the total n. The mean is then calculated as shown in Figure 4-3.
This is the same result as you would reach by adding each score (1+1+1+1+ . . .) and dividing by 26.
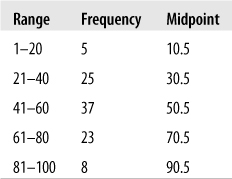
The mean for grouped data, in which data has been tabulated by range and exact values are not known, is calculated in a similar manner. Because we don’t know the exact values for each case (we know, for instance, that 5 values fell into the range of 1–20 but not the specific values for those five cases), for the purposes of calculation we use the midpoint of the range as a stand-in for the specific values. Therefore, to calculate the mean, we first calculate this midpoint for each range and then multiply it by the frequency of values in the range. To calculate the midpoint for a range, add the first and last values in the range and divide by 2. For instance, for the 1–20 range, the midpoint is:
A mean calculated in this way is called a grouped mean. A grouped mean is not as precise as the mean calculated from the original data points, but it is often your only option if the original values are not available. Consider the following grouped data set in Figure 4-4.
The mean is calculated by multiplying the midpoint of each interval by the number of values in the interval (the frequency) and dividing by the total frequency, as shown in Figure 4-5.
One way to lessen the influence of outliers is by calculating a trimmed mean, also known as a Winsorized mean. As the name implies, a trimmed mean is calculated by trimming or discarding a certain percentage of the extreme values in a distribution and then calculating the mean of the remaining values. The purpose is to calculate a mean that represents most of the values well and is not unduly influenced by extreme values. Consider the example of the second population with five members previously cited, with values 100, 115, 93, 102, and 297. The mean of this population is distorted by the influence of one very large value, so we calculate a trimmed mean by dropping the highest and lowest values (equivalent to dropping the lowest and highest 20% of values). The trimmed mean is calculated as:
The value of 105.7 is much closer to the typical values in the distribution than 141.4, the value of the mean including all the data values. Of course, we seldom would be working with a population with only five members, but the principle applies to large populations as well. Usually, a specific percentage of the data values are trimmed from the extremes of the distribution, and this decision would have to be reported to make it clear what the calculated mean actually represents.
The mean can also be calculated for dichotomous data by using 0–1 coding, in which case the mean is equivalent to the percentage of values with the number 1. Suppose we have a population of 10 subjects, 6 of whom are male and 4 of whom are female, and we have coded males as 1 and females as 0. Computing the mean will give us the percentage of males in the population:
The median of a data set is the middle value when the values are ranked in ascending or descending order. If there are n values, the median is formally defined as the (n +1)/2th value, so if n = 7, the middle value is the (7+1)/2th or fourth value. If there is an even number of values, the median is the average of the two middle values. This is formally defined as the average of the (n /2)th and ((n /2)+1)th value. If there are six values, the median is the average of the (6/2)th and ((6/2)+1)th value, or the third and fourth values. Both techniques are demonstrated here:
| Odd number (5) of values: 1, 4, 6, 6, 10; Median = 6 because (5+1)/2 = 3, and 6 is the third value in the ordered list. |
| Even number (6) of values: 1, 3, 5, 6, 10, 15; Median = (5+6)/2 = 5.5 because 6/2 = 3 and [(6/2) +1] = 4, and 5 and 6 are the third and fourth values in the ordered list. |
The median is a better measure of central tendency than the mean for data that is asymmetrical or contains outliers. This is because the median is based on the ranks of data points rather than their actual values, and by definition, half of the data values in a distribution lie below the median and half above the median, without regard to the actual values in question. Therefore, it does not matter whether the data set contains some extremely large or small values because they will not affect the median more than less extreme values. For instance, the median of all three of the following distributions is 4:
| Distribution A: 1, 1, 3, 4, 5, 6, 7 |
| Distribution B: 0.01, 3, 3, 4, 5, 5, 5 |
| Distribution C: 1, 1, 2, 4, 5, 100, 2000 |
Of course, the median is not always an appropriate measure to describe a population or a sample. This is partly a judgment call; in this example, the median seems reasonably representative of the data values in Distributions A and B, but perhaps not for Distribution C, whose values are so disparate that any single summary measure can be misleading.
A third common measure of central tendency is the mode, which refers to the most frequently occurring value. The mode is most often useful in describing ordinal or categorical data. For instance, imagine that the following numbers reflect the favored news sources of a group of college students, where 1 = newspapers, 2 = television, and 3 = Internet:
We can see that the Internet is the most popular source because 3 is the modal (most common) value in this data set.
When modes are cited for continuous data, usually a range of values is referred to as the mode (because with many values, as is typical of continuous data, there might be no single value that occurs substantially more often than any other). If you intend to do this, you should decide on the categories in advance and use standard ranges if they exist. For instance, age for adults is often collected in ranges of 5 or 10 years, so it might be the case that in a given data set, divided into ranges of 10 years, the modal range was ages 40–49 years.
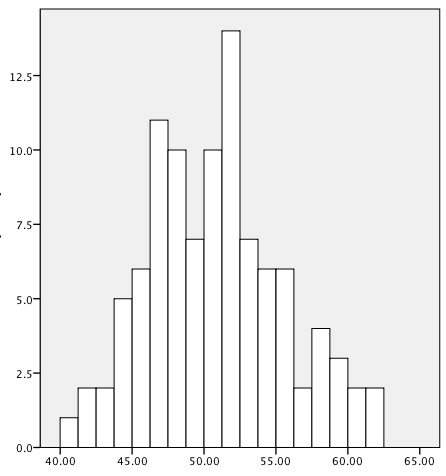
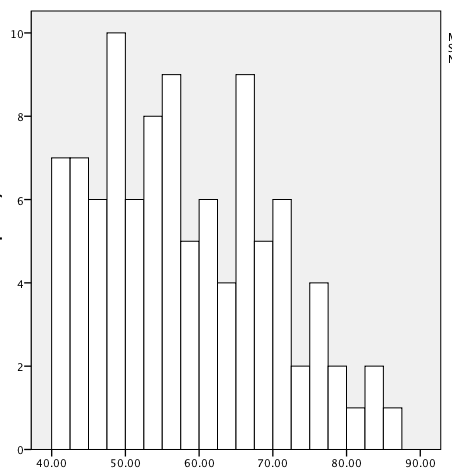
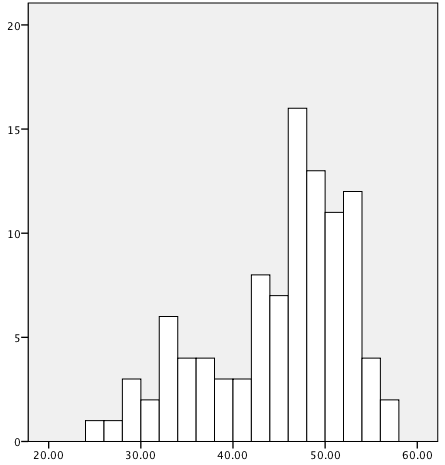
In a perfectly symmetrical distribution (such as the normal distribution, discussed in Chapter 3), the mean, median, and mode are identical. In an asymmetrical or skewed distribution, these three measures will differ, as illustrated in the data sets graphed as histograms in Figures 4-6, 4-7, and 4-8. To facilitate calculating the mode, we have also divided each data set into ranges of 5 (35–39.99, 40–44.99, etc.).
The data in Figure 4-6 is approximately normal and symmetrical with a mean of 50.88 and a median of 51.02; the most common range is 50.00–54.99 (37 cases), followed by 45.00–49.99 (34 cases). In this distribution, the mean and median are very close to each other, and the two most common ranges also cluster around the mean.
The data in Figure 4-7 is right skewed; the mean is 58.18, and the median is 56.91; a mean higher than a median is common for right-skewed data because the extreme higher values pull the mean up but do not have the same effect on the median. The modal range is 45.00–49.99 with 16 cases; however, several other ranges have 14 cases, making them very close in terms of frequency to the modal range and making the mode less useful in describing this data set.
The data in Figure 4-8 is left skewed; the mean is 44.86, and the median is 47.43. A mean lower than the median is typical of left-skewed data because the extreme lower values pull the mean down, whereas they do not have the same effect on the median. The skew in Figure 4-8 is greater than that in Figure 4-7, and this is reflected in the greater difference between the mean and median in Figure 4-8 as compared to Figure 4-7. The modal range for Figure 4-8 is 45.00–49.99.
Dispersion refers to how variable or spread out data values are. For this reason, measures of dispersions are sometimes called measures of variability or measures of spread. Knowing the dispersion of data can be as important as knowing its central tendency. For instance, two populations of children may both have mean IQs of 100, but one could have a range of 70 to 130 (from mild retardation to very superior intelligence) whereas the other has a range of 90 to 110 (all within the normal range). The distinction could be important, for instance, to educators, because despite having the same average intelligence, the range of IQ scores for these two groups suggests that they might have different educational and social needs.
The simplest measure of dispersion is the range, which is simply the difference between the highest and lowest values. Often the minimum (smallest) and maximum (largest) values are reported as well as the range. For the data set (95, 98, 101, 105), the minimum is 95, the maximum is 105, and the range is 10 (105–95). If there are one or a few outliers in the data set, the range might not be a useful summary measure. For instance, in the data set (95, 98, 101, 105, 210), the range is 115, but most of the numbers lie within a range of 10 (95–105). Inspection of the range for any variable is a good data screening technique; an unusually wide range or extreme minimum or maximum values might warrant further investigation. Extremely high or low values or an unusually wide range of values might be due to reasons such as data entry error or to inclusion of a case that does not belong to the population under study. (Information from an adult might have been included mistakenly in a data set concerned with children.)
The interquartile range is an alternative measure of dispersion that is less influenced than the range by extreme values. The interquartile range is the range of the middle 50% of the values in a data set, which is calculated as the difference between the 75th and 25th percentile values. The interquartile range is easily obtained from most statistical computer programs but can also be calculated by hand, using the following rules (n = the number of observations, k the percentile you wish to find):
Rank the observations from smallest to largest.
If (nk)/100 is an integer (a round number with no decimal or fractional part), the kth percentile of the observations is the average of the ((nk)/100)th and ((nk)/100 + 1)th largest observations.
If (nk)/100 is not an integer, the kth percentile of the observation is the (j + 1)th largest measurement, where j is the largest integer less than (nk)/100.
Calculate the interquartile range as the difference between the 75th and 25th percentile measurements.
Consider the following data set with 13 observations (1, 2, 3, 5, 7, 8, 11, 12, 15, 15, 18, 18, 20):
First, we want to find the 25th percentile, so k = 25.
We have 13 observations, so n = 13.
(nk)/100 = (25 × 13)/100 = 3.25, which is not an integer, so we will use the second method (#3 in the preceding list).
j = 3 (the largest integer less than (nk)/100, that is, less than 3.25).
Therefore, the 25th percentile is the ( j + 1)th or 4th observation, which has the value 5.
We can follow the same steps to find the 75th percentile:
(nk)/100 = (75*13)/100 = 9.75, not an integer.
j = 9, the smallest integer less than 9.75.
Therefore, the 75th percentile is the 9 + 1 or 10th observation, which has the value 15.
Therefore, the interquartile range is (15 − 5) or 10.
The resistance of the interquartile range to outliers should be clear. This data set has a range of 19 (20 − 1) and an interquartile range of 10; however, if the last value was 200 instead of 20, the range would be 199 (200 − 1), but the interquartile range would still be 10, and that number would better represent most of the values in the data set.
The most common measures of dispersion for continuous data are the variance and standard deviation. Both describe how much the individual values in a data set vary from the mean or average value. The variance and standard deviation are calculated slightly differently depending on whether a population or a sample is being studied, but basically the variance is the average of the squared deviations from the mean, and the standard deviation is the square root of the variance. The variance of a population is signified by σ2 (pronounced “sigma-squared”; σ is the Greek letter sigma) and the standard deviation as σ, whereas the sample variance and standard deviation are signified by s2 and s, respectively.
The deviation from the mean for one value in a data set is calculated as (xi − µ) where xi is value i from the data set and µ is the mean of the data set. If working with sample data, the principle is the same, except that you subtract the mean of the sample (![]() ) from the individual data values rather than the mean of the population. Written in summation notation, the formula to calculate the sum of all deviations from the mean for the variable x for a population with n members is shown in Figure 4-9.
) from the individual data values rather than the mean of the population. Written in summation notation, the formula to calculate the sum of all deviations from the mean for the variable x for a population with n members is shown in Figure 4-9.
Unfortunately, this quantity is not useful because it will always equal zero, a result that is not surprising if you consider that the mean is computed as the average of all the values in the data set. This may be demonstrated with the tiny data set (1, 2, 3, 4, 5). First, we calculate the mean:
Then we calculate the sum of the deviations from the mean, as shown in Figure 4-10.
To get around this problem, we work with squared deviations, which by definition are always positive. To get the average deviation or variance for a population, we square each deviation, add them up, and divide by the number of cases, as shown in Figure 4-11.
The sample formula for the variance requires dividing by n − 1 rather than n; the reasons are technical and have to do with degrees of freedom and unbiased estimation. (For a detailed discussion, see the Wilkins article listed in Appendix C.) The formula for the variance of a sample, notated as s2, is shown in Figure 4-12.
Continuing with our tiny data set with values (1, 2, 3, 4, 5), with a mean value of 3, we can calculate the variance for this population as shown in Figure 4-13.
If we consider these numbers to be a sample rather than a population, the variance would be computed as shown in Figure 4-14.
Note that because of the different divisor, the sample formula for the variance will always return a larger result than the population formula, although if the sample size is close to the population size, this difference will be slight.
Because squared numbers are always positive (outside the realm of imaginary numbers), the variance will always be equal to or greater than 0. (The variance would be zero only if all values of a variable were the same, in which case the variable would really be a constant.) However, in calculating the variance, we have changed from our original units to squared units, which might not be convenient to interpret. For instance, if we were measuring weight in pounds, we would probably want measures of central tendency and dispersion expressed in the same units rather than having the mean expressed in pounds and variance in squared pounds. To get back to the original units, we take the square root of the variance; this is called the standard deviation and is signified by σ for a population and s for a sample.
For a population, the formula for the standard deviation is shown in Figure 4-15.
Note that this is simply the square root of the formula for variance. In the preceding example, the standard deviation can be found as shown in Figure 4-16.
The formula for the sample standard deviation is shown in Figure 4-17.
As with the population standard deviation, the sample standard deviation is the square root of the sample variance (Figure 4-18).
In general, for two groups of the same size and measured with the same units (e.g., two groups of people, each of size n = 30 and both weighed in pounds), we can say that the group with the larger variance and standard deviation has more variability among their scores. However, the unit of measure affects the size of the variance, which can make it tricky to compare the variability of factors measured in different units. To take an obvious example, a set of weights expressed in ounces would have a larger variance and standard deviation than the same weights measured in pounds. When comparing completely different units, such as height in inches and weight in pounds, it is even more difficult to compare variability. The coefficient of variation (CV), a measure of relative variability, gets around this difficulty and makes it possible to compare variability across variables measured in different units. The CV is shown here using sample notation but could be calculated for a population by substituting σ for s. The CV is calculated by dividing the standard deviation by the mean and then multiplying by 100, as shown in Figure 4-19.
For the previous example, this would be calculated as shown in Figure 4-20.
The CV cannot be calculated if the mean of the data is 0 (because you cannot divide by 0) and is most useful when the variable in question has only positive values. If a variable has both positive and negative values, the mean can be close to zero although the data actually has quite a broad range, and this can produce a misleading CV value because the denominator will be a small number, potentially producing a large CV value even if the standard deviation is fairly moderate.
The usefulness of the CV should be clear by considering the same data set as expressed in feet and inches; for instance, 60 inches is the same as 5 feet. The data as expressed in feet has a mean of 5.5566 and a standard deviation of 0.2288; the same data as expressed in inches has a mean of 66.6790 and a standard deviation of 2.7453. However, the CV is not affected by the change in units and produces the same result either way, except for rounding error:
| 5.5566/0.2288 = 24.2858 (data in feet) |
| 66.6790/2.7453 = 24.2884 (data in inches) |
There is no absolute agreement among statisticians about how to define outliers, but nearly everyone agrees that it is important that they be identified and that appropriate analytical techniques be used for data sets that contain outliers. An outlier is a data point or observation whose value is quite different from the others in the data set being analyzed. This is sometimes described as a data point that seems to come from a different population or is outside the typical pattern of the other data points. Suppose you are studying educational achievement in a sample or population, and most of your subjects have completed from 12 to 16 years of schooling (12 years = high school graduation, 16 years = university graduation). However, one of your subjects has a value of 0 for this variable (implying that he has no formal education at all) and another has a value of 26 (implying many years of post-graduate education). You will probably consider these two cases to be outliers because they have values far removed from the other data in your sample of population. Identification and analysis of outliers is an important preliminary step in many types of data analysis because the presence of just one or two outliers can completely distort the value of some common statistics, such as the mean.
It’s also important to identify outliers because sometimes they represent data entry errors. In the preceding example, the first thing to do is check whether the data was entered correctly; perhaps the correct values are 10 and 16, respectively. The second thing to do is investigate whether the cases in question actually belong to the same population as the other cases. For instance, does the 0 refer to the years of education of an infant when the data set was supposed to contain only information about adults?
If neither of these simple fixes solves the problem, it is necessary to make a judgment call (possibly in consultation with others involved in the research) about what to do with the outliers. It is possible to delete cases with outliers from the data set before analysis, but the acceptability of this practice varies from field to field. Sometimes a statistical fix already exists, such as the trimmed mean previously described, although the acceptability of such fixes also varies from one field to the next. Other possibilities are to transform the data (discussed in Chapter 3) or use nonparametric statistical techniques (discussed in Chapter 13), which are less influenced by outliers.
Various rules of thumb have been developed to make the identification of outliers more consistent. One common definition of an outlier, which uses the concept of the interquartile range (IQR), is that mild outliers are those lower than the 25th quartile minus 1.5 × IQR or greater than the 75th quartile plus 1.5 × IQR. Cases this extreme are expected in about 1 in 150 observations in normally distributed data. Extreme outliers are similarly defined with the substitution of 3 × IQR for 1.5 × IQR; values this extreme are expected about once per 425,000 observations in normally distributed data.
There are innumerable graphic methods to present data, from the basic techniques included with spreadsheet software such as Microsoft Excel to the extremely specific and complex methods available in computer languages such as R. Entire books have been written on the use and misuse of graphics in presenting data, and the leading (if also controversial) expert in this field is Edward Tufte, a Yale professor (with a Master’s degree in statistics and a PhD in political science). His most famous work is The Visual Display of Quantitative Information (listed in Appendix C), but all of Tufte’s books are worthwhile reading for anyone seriously interested in the graphic display of data. It would be impossible to cover even a fraction of the available methods to display data in this section, so instead, a few of the most common methods are presented, including a discussion of issues concerning each.
It’s easy to get carried away with fancy graphical presentations, particularly because spreadsheets and statistical programs have built-in routines to create many types of graphs and charts. Tufte’s term for graphic material that does not convey information is “chartjunk,” which concisely conveys his opinion of such presentations. The standards for what is considered junk vary from one field of endeavor to another, but as a general rule, it is wise to use the simplest type of chart that clearly presents your information while remaining aware of the expectations and standards within your chosen profession or field of study.
The first question to ask when considering how best to display data is whether a graphical method is needed at all. It’s true that in some circumstances a picture may be worth a thousand words, but at other times, frequency tables do a better job than graphs at presenting information. This is particularly true when the actual values of the numbers in different categories, rather than the general pattern among the categories, are of primary interest. Frequency tables are often an efficient way to present large quantities of data and represent a middle ground between text (paragraphs describing the data values) and pure graphics (such as a histogram).
Suppose a university is interested in collecting data on the general health of their entering classes of freshmen. Because obesity is a matter of growing concern in the United States, one of the statistics they collect is the Body Mass Index (BMI), calculated as weight in kilograms divided by squared height in meters. The BMI is not an infallible measure. For instance, athletes often measure as either underweight (distance runners, gymnasts) or overweight or obese (football players, weight throwers), but it’s an easily calculated measurement that is a reliable indicator of a healthy or unhealthy body weight for many people.
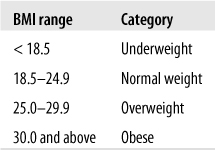
The BMI is a continuous measure, but it is often interpreted in terms of categories, using commonly accepted ranges. The ranges for the BMI shown in Figure 4-21, established by the Centers for Disease Control and Prevention (CDC) and the World Health Organization (WHO), are generally accepted as useful and valid.
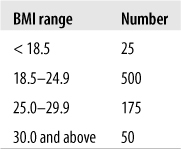
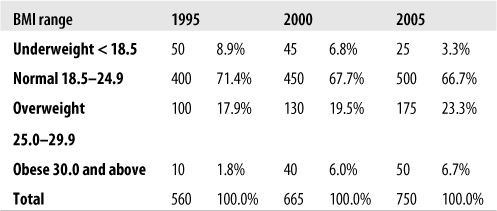
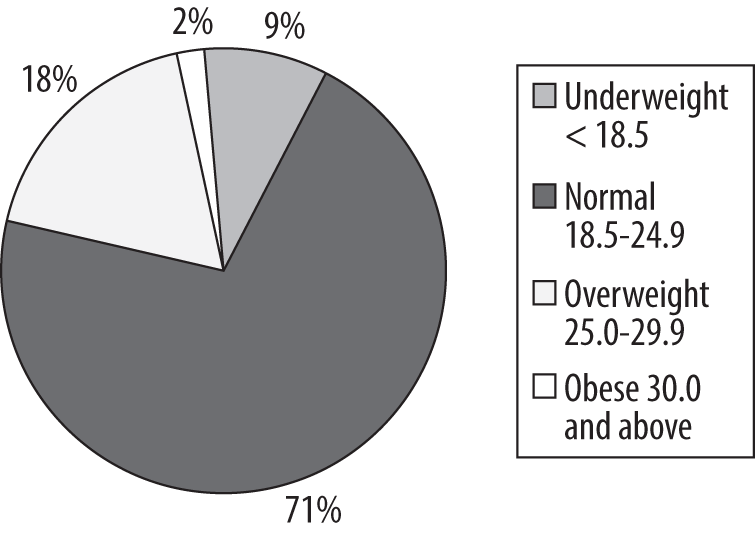
Now consider Figure 4-22, an entirely fictitious list of BMI classifications for entering freshmen.
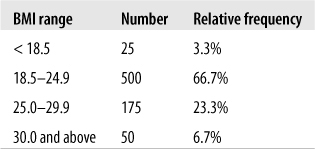
This simple table tells us at a glance that most of the freshman are of normal body weight or are moderately overweight, with a few who are underweight or obese. Note that this table presents raw numbers or counts for each category, which are sometimes referred to as absolute frequencies; these numbers tell you how often each value appears, which can be useful if you are interested in, for instance, how many students might require obesity counseling. However, absolute frequencies don’t place the number of cases in each category into any kind of context. We can make this table more useful by adding a column for relative frequency, which displays the percent of the total represented by each category. The relative frequency is calculated by dividing the number of cases in each category by the total number of cases (750) and multiplying by 100. Figure 4-23 shows the both the absolute and the relative frequencies for this data.
Note that relative frequencies should add up to approximately 100%, although the total might be slightly higher or lower due to rounding error.
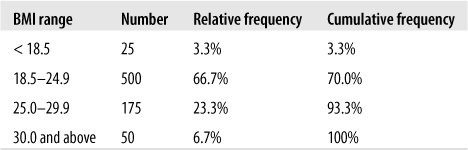
We can also add a column for cumulative frequency, which shows the relative frequency for each category and those below it, as in Figure 4-24. The cumulative frequency for the final category should always be 100% except for rounding error.
Cumulative frequency tells us at a glance, for instance, that 70% of the entering class is normal weight or underweight. This is particularly useful in tables with many categories because it allows the reader to ascertain specific points in the distribution quickly, such as the lowest 10%, the median (50% of the cumulative frequency), or the top 5%.
You can also construct frequency tables to make comparisons between groups. You might be interested, for instance, in comparing the distribution of BMI in male and female freshmen or for the class that entered in 2005 versus the entering classes of 2000 and 1995. When making comparisons of this type, raw numbers are less useful (because the size of the classes can differ) and relative and cumulative frequencies more useful. Another possibility is to create graphic presentations such as the charts described in the next section, which can make such comparisons clearer.
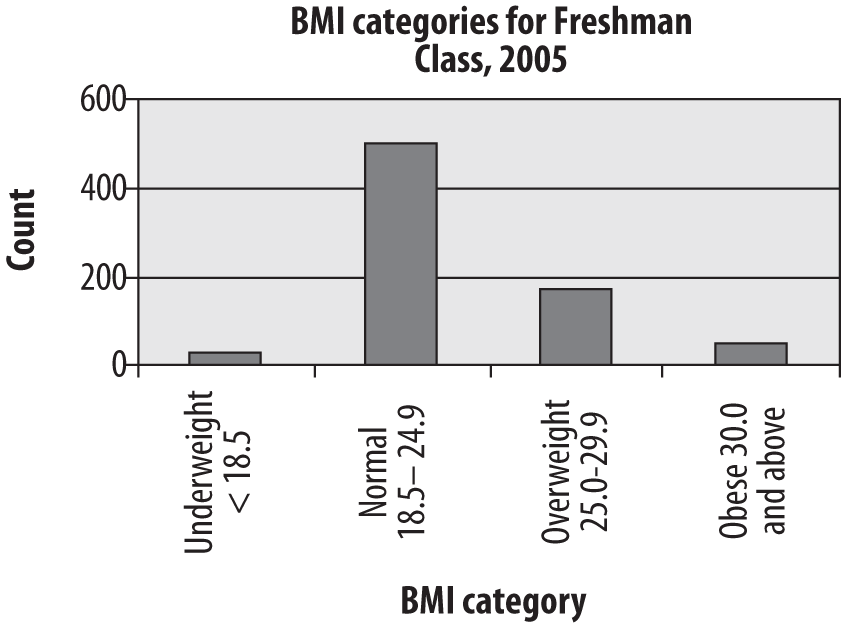
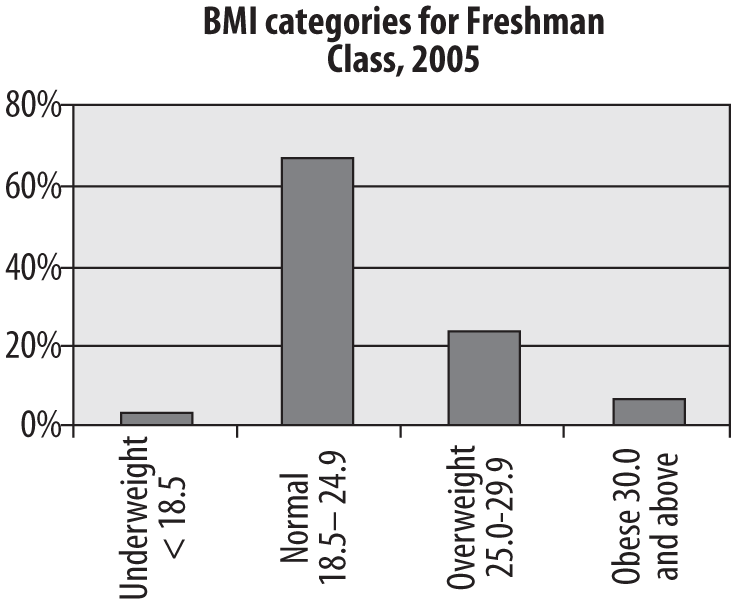
The bar chart is particularly appropriate for displaying discrete data with only a few categories, as in our example of BMI among the freshman class. The bars in a bar chart are customarily separated from each other so they do not suggest continuity; although in this case, our categories are based on categorizing a continuous variable, they could equally well be completely nominal categories such as favorite sport or major field of study. Figure 4-25 shows the freshman BMI information presented in a bar chart. (Unless otherwise noted, the charts presented in this chapter were created using Microsoft Excel.)
Absolute frequencies are useful when you need to know the number of people in a particular category, whereas relative frequencies are more useful when you need to know the relationship of the numbers in each category. Relative frequencies are particularly useful, as we will see, when comparing multiple groups, for instance whether the proportion of obese students is rising or falling over the years. For a simple bar chart, the absolute versus relative frequencies question is less critical, as can be seen by comparing a bar chart of the student BMI data, presented as relative frequencies in Figure 4-26 with the same data presented as absolute frequencies in Figure 4-25. Note that the two charts are identical except for the y-axis (vertical axis) labels, which are frequencies in Figure 4-25 and percentages in Figure 4-26.
The concept of relative frequencies becomes even more useful if we compare the distribution of BMI categories over several years. Consider the fictitious frequency information in Figure 4-27.
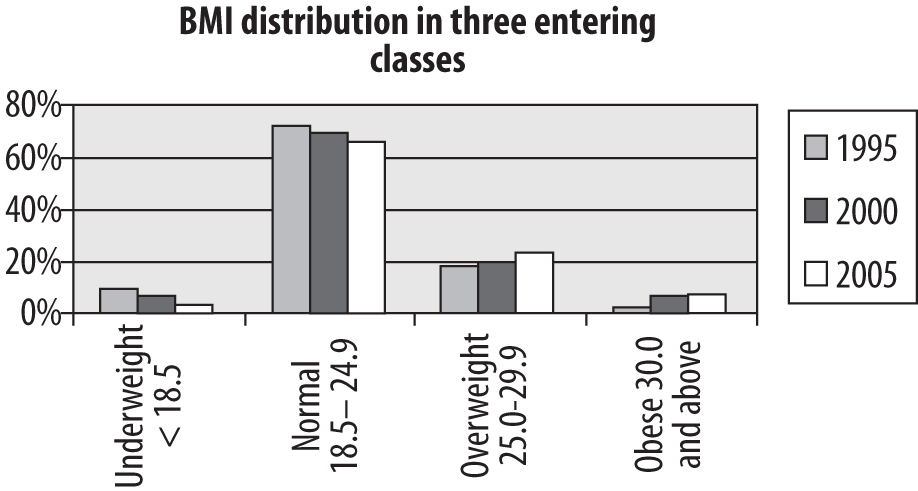
Because the class size is different in each year, the relative frequencies (percentages) are most useful in observing trends in weight category distribution. In this case, there has been a clear decrease in the proportion of underweight students and an increase in the number of overweight and obese students. This information can also be displayed using a bar chart, as in Figure 4-28.
This is a grouped bar chart, which shows that there is a small but definite trend over 10 years toward fewer underweight and normal weight students and more overweight and obese students (reflecting changes in the American population at large). Bear in mind that creating a chart is not the same thing as conducting a statistical test, so we can’t tell from this chart alone whether these differences are statistically significant.
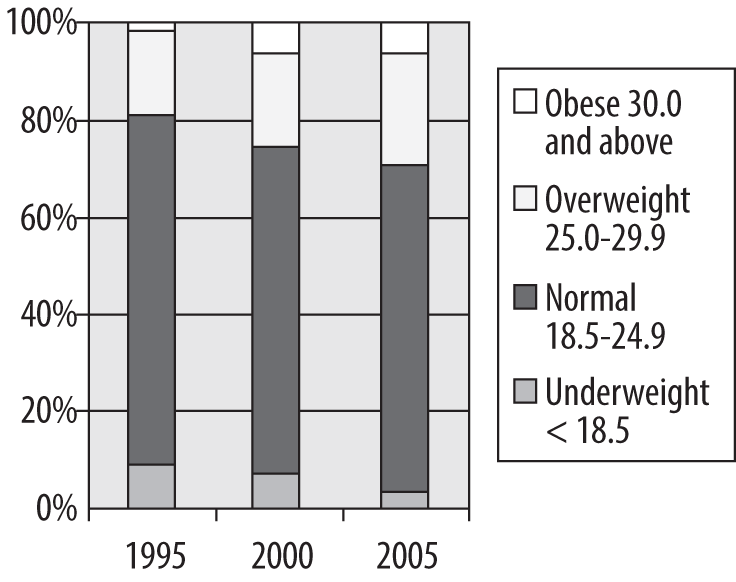
Another type of bar chart, which emphasizes the relative distribution of values within each group (in this case, the relative distribution of BMI categories in three entering classes), is the stacked bar chart, illustrated in Figure 4-29.
In this type of chart, each bar represents one year of data, and each bar totals to 100%. The relative proportion of students in each category can be seen at a glance by comparing the proportion of area within each bar allocated to each category. This arrangement facilitates comparison in multiple data series (in this case, the three years). It is immediately clear that the proportion of underweight students has declined, and the proportion of overweight and obese students has increased over time.
The familiar pie chart presents data in a manner similar to the stacked bar chart: it shows graphically what proportion each part occupies of the whole. Pie charts, like stacked bar charts, are most useful when there are only a few categories of information and the differences among those categories are fairly large. Many people have particularly strong opinions about pie charts, and although pie charts are still commonly used in some fields, they have also been aggressively denounced in others as uninformative at best and potentially misleading at worst. So you must make your own decision based on context and convention; I will present the same BMI information in pie chart form (Figure 4-30), and you may be the judge of whether this is a useful way to present the data. Note that this is a single pie chart, showing one year of data, but other options are available, including side-by-side charts (to facilitate comparison of the proportions of different groups) and exploded sections (to show a more detailed breakdown of categories within a segment).
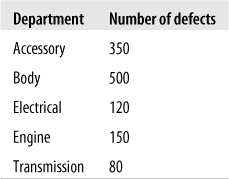
The Pareto chart or Pareto diagram combines the properties of a bar chart and a line chart; the bars display frequency and relative frequency, whereas the line displays cumulative frequency. The great advantage of a Pareto chart is that it is easy to see which factors are most important in a situation and, therefore, to which factors most attention should be directed. For instance, Pareto charts are often used in industrial contexts to identify factors that are responsible for the preponderance of delays or defects in the manufacturing process. In a Pareto chart, the bars are ordered in descending frequency from left to right (so the most common cause is the furthest to the left and the least common the furthest to the right), and a cumulative frequency line is superimposed over the bars (so you see, for instance, how many factors are involved in 80% of production delays). Consider the hypothetical data set shown in Figure 4-31, which displays the number of defects traceable to different aspects of the manufacturing process in an automobile factory.
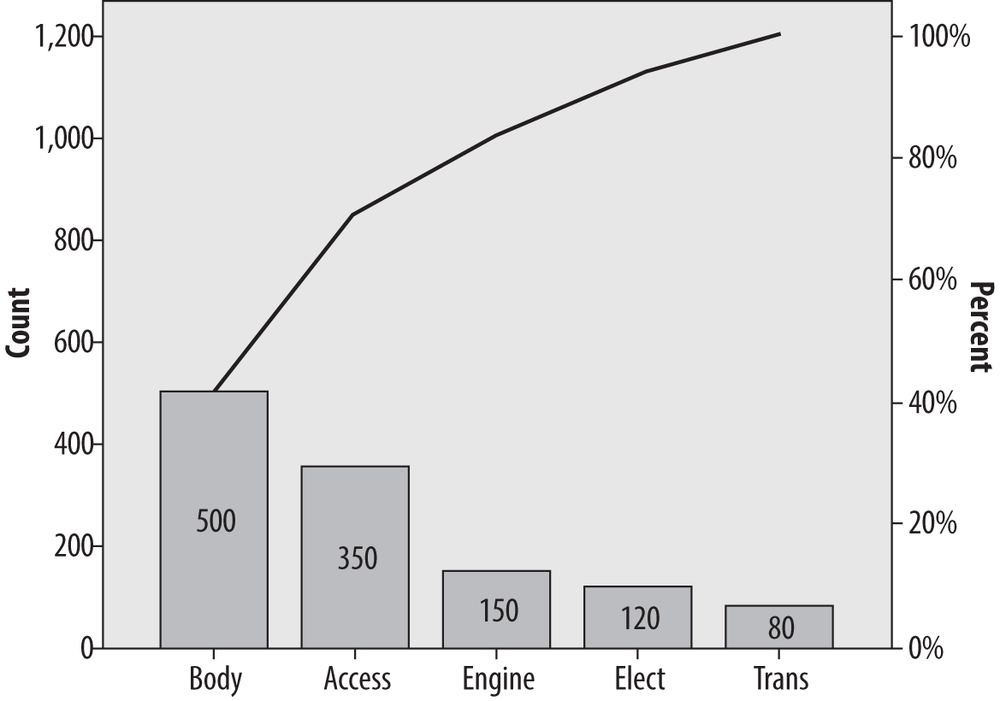
Although we can see that the Accessory and Body departments are responsible for the greatest number of defects, it is not immediately obvious what proportion of defects can be traced to them. Figure 4-32, which displays the same information presented in a Pareto chart (produced using SPSS), makes this clearer.
This chart tells us not only that the most common causes of defects are in the Body and Accessory manufacturing processes but also that together they account for about 75% of defects. We can see this by drawing a straight line from the bend in the cumulative frequency line (which represents the cumulative number of defects from the two largest sources, Body and Accessory) to the right-hand y-axis. This is a simplified example and violates the 80:20 rule (discussed in the next sidebar about Vilfredo Pareto) because only a few major causes of defects are shown. In a more realistic example, there might be 30 or more competing causes, and the Pareto chart is a simple way to sort them out and decide which processes should be the focus of improvement efforts. This simple example does serve to display the typical characteristics of a Pareto chart. The bars are sorted from highest to lowest, the frequency is displayed on the left-hand y-axis and the percent on the right, and the actual number of cases for each cause are displayed within each bar.
The types of charts discussed so far are most appropriate for displaying categorical data. Continuous data has its own set of graphic display methods. One of the simplest ways to display continuous data graphically is the stem-and-leaf plot, which can easily be created by hand and presents a quick snapshot of a data distribution. To make a stem-and-leaf plot, divide your data into intervals (using your common sense and the level of detail appropriate to your purpose) and display each data point by using two columns. The stem is the leftmost column and contains one value per row, and the leaf is the rightmost column and contains one digit for each case belonging to that row. This creates a plot that displays the actual values of the data set but also assumes a shape indicating which ranges of values are most common. The numbers can represent multiples of other numbers (for instance, units of 10,000 or of 0.01) if appropriate, given the data values in question.
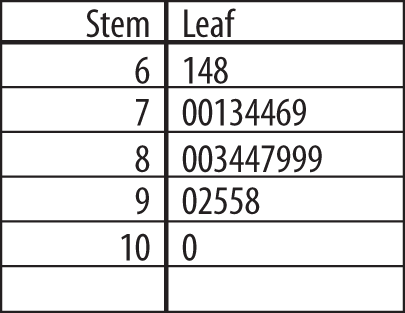
Here’s a simple example. Suppose we have the final exam grades for 26 students and want to present them graphically. These are the grades:
The logical division is units of 10 points, for example, 60–69, 70–79, and so on, so we construct the stem of the digits 6, 7, 8, 9 (the tens place for those of you who remember your grade school math) and create the leaf for each number with the digit in the ones place, ordered left to right from smallest to largest. Figure 4-33 shows the final plot.
This display not only tells us the actual values of the scores and their range (61–100) but the basic shape of their distribution as well. In this case, most scores are in the 70s and 80s, with a few in the 60s and 90s, and one is 100. The shape of the leaf side is in fact a crude sort of histogram (discussed later) rotated 90 degrees, with the bars being units of 10.
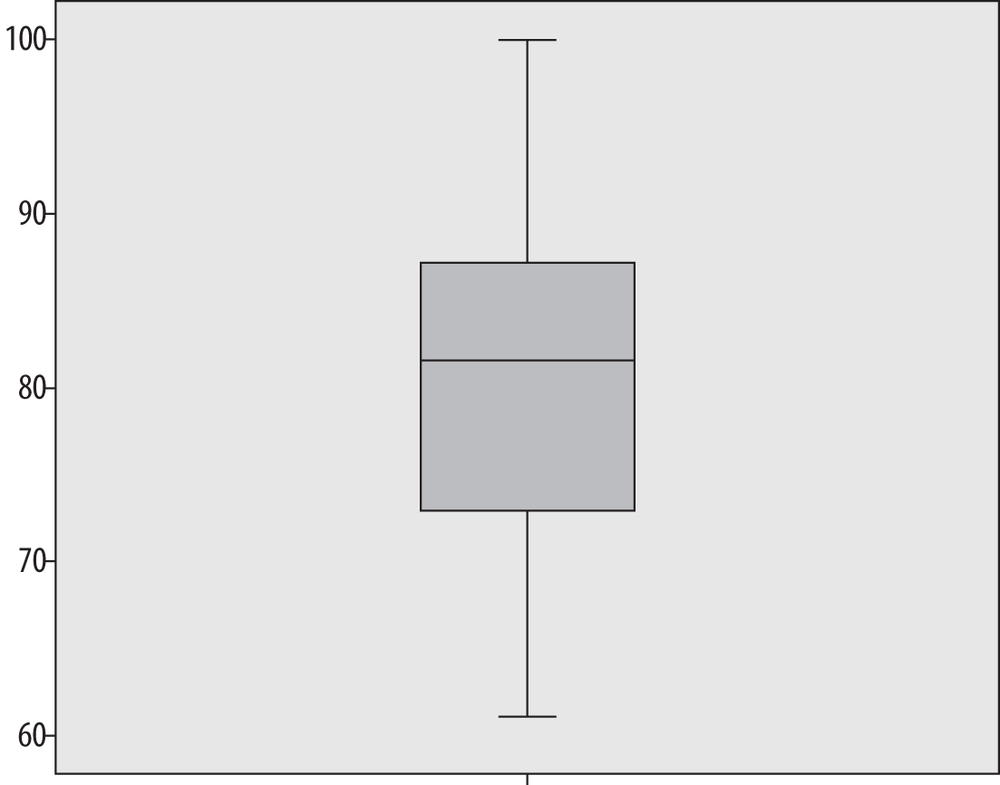
The boxplot, also known as the hinge plot or the box-and-whiskers plot, was devised by the statistician John Tukey as a compact way to summarize and display the distribution of a set of continuous data. Although boxplots can be drawn by hand (as can many other graphics, including bar charts and histograms), in practice they are usually created using software. Interestingly, the exact methods used to construct boxplots vary from one software package to another, but they are always constructed to highlight five important characteristics of a data set: the median, the first and third quartiles (and hence the interquartile range as well), and the minimum and maximum. The central tendency, range, symmetry, and presence of outliers in a data set are visible at a glance from a boxplot, whereas side-by-side boxplots make it easy to make comparisons among different distributions of data. Figure 4-34 is a boxplot of the final exam grades used in the preceding stem-and-leaf plot.
The dark line represents the median value, in this case, 81.5. The shaded box encloses the interquartile range, so the lower boundary is the first quartile (25th percentile) of 72.5, and the upper boundary is the third quartile (75th percentile) of 87.75. Tukey called these quartiles hinges, hence the name hinge plot. The short horizontal lines at 61 and 100 represent the minimum and maximum values, and together with the lines connecting them to the interquartile range box, they are called whiskers, hence the name box-and-whiskers plot. We can see at a glance that this data set is symmetrical because the median is approximately centered within the interquartile range, and the interquartile range is located approximately centrally within the complete range of the data.
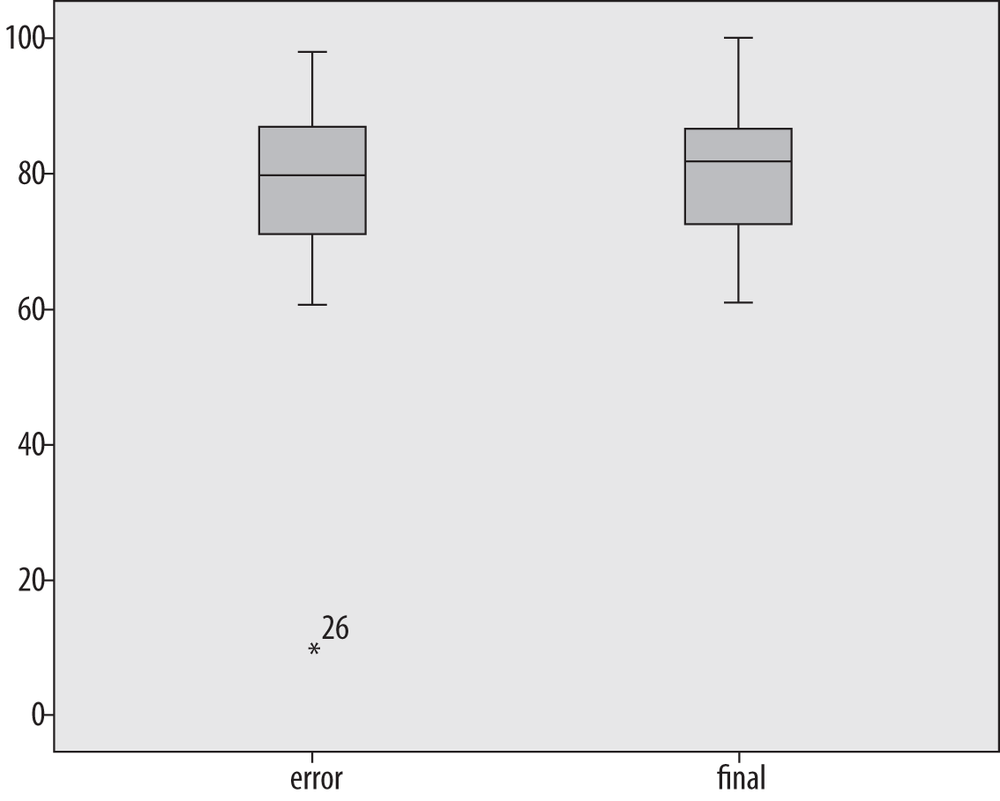
This data set contains no outliers, that is, no numbers that are far outside the range of the other data points. To demonstrate a boxplot that contains outliers, I have changed the score of 100 in this data set to 10. Figure 4-35 shows the boxplots of the two data sets side by side. (The boxplot for the correct data is labeled “final,” whereas the boxplot with the changed value is labeled “error.”)
Note that except for the single outlier value, the two data sets look very similar; this is because the median and interquartile range are resistant to influence by extreme values. The outlying value is designated with an asterisk and labeled with its case number (26); the latter feature is not included in every statistical package.
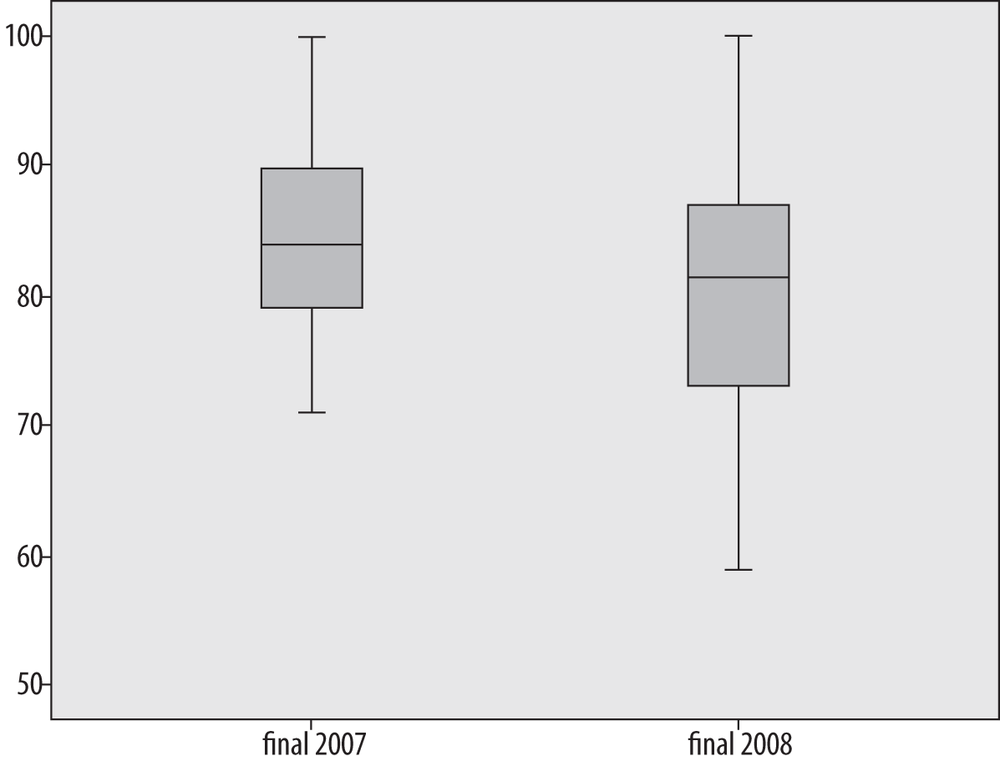
Boxplots are often used to compare two or more real data sets side by side. Figure 4-36 shows a comparison of two years of final exam grades from 2007 and 2008, labeled “final2007” and “final2008,” respectively.
Without looking at any of the actual grades, I can see several differences between the two years:
The highest scores are the same in both years.
The lowest score is much lower in 2008 than in 2007.
There is a greater range of scores in 2008, both in the interquartile range (middle 50% of the scores) and overall.
The median is slightly lower in 2008.
That the highest score was the same in both years is not surprising because this exam had a range of 0–100, and at least one student achieved the highest score in both years. This is an example of a ceiling effect, which exists when scores or measurements can be no higher than a particular number and people actually achieve that score. The analogous condition, if a score can be no lower than a specified number, is called a floor effect. In this case, the exam had a floor of 0 (the lowest possible score), but because no one achieved that score, no floor effect is present in the data.
The histogram is another popular choice for displaying continuous data. A histogram looks similar to a bar chart, but in a histogram, the bars (also known as bins because you can think of them as bins into which values from a continuous distribution are sorted) touch each other, unlike the bars in a bar chart. Histograms also tend to have a larger number of bars than do bar charts. Bars in a histogram do not have to be the same width, although frequently they are. The x-axis (vertical axis) in a histogram represents a scale rather than simply a series of labels, and the area of each bar represents the proportion of values that are contained in that range.
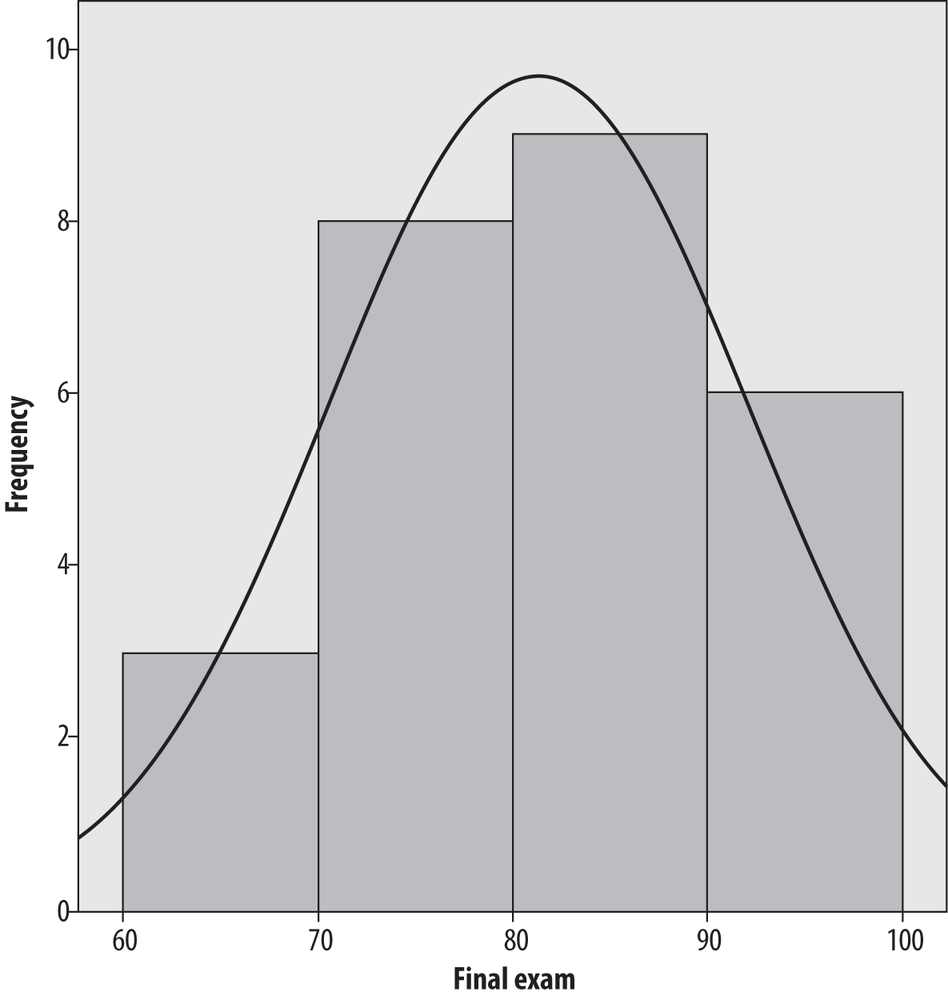
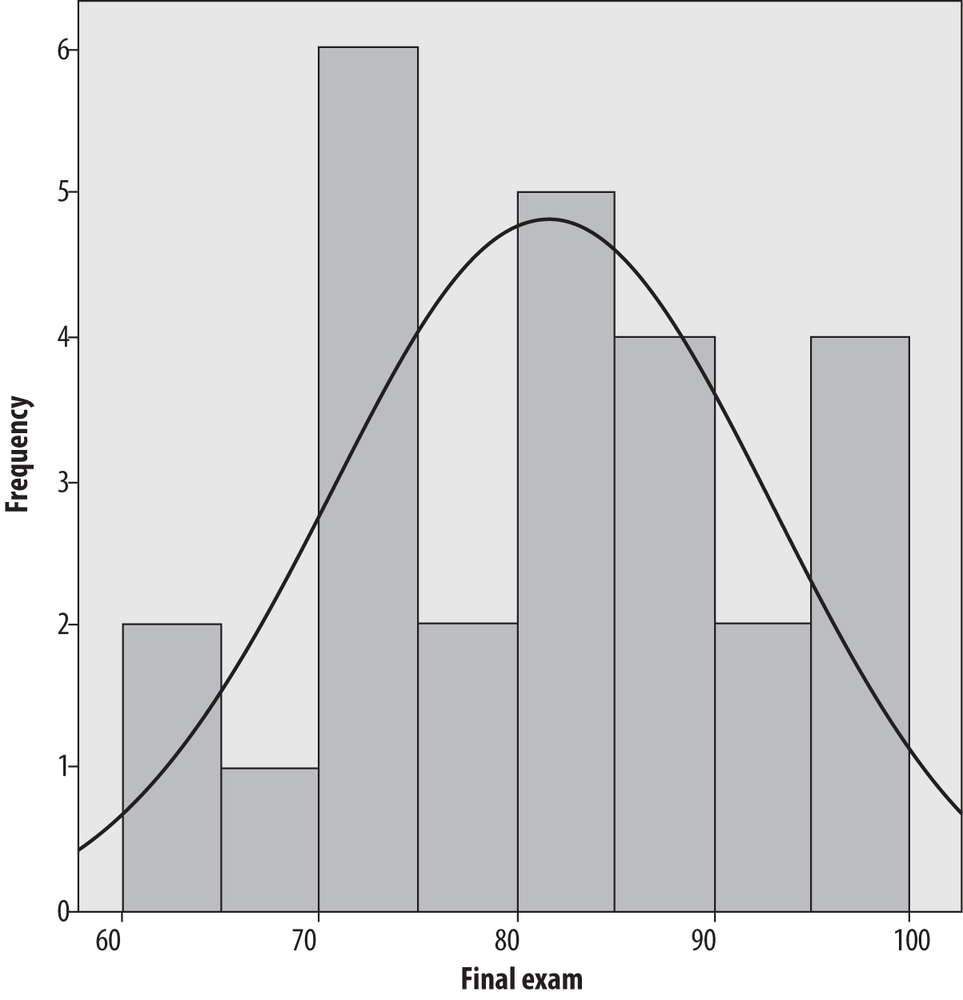
Figure 4-37 shows the final exam data presented as a histogram created in SPSS with four bars of width ten and with a normal distribution superimposed. Note that the shape of this histogram looks quite similar to the shape of the stem-and-leaf plot of the same data (Figure 4-33), but rotated 90 degrees.
The normal distribution is discussed in detail in Chapter 3; for now, it is a commonly used theoretical distribution that has the familiar bell shape shown here. The normal distribution is often superimposed on histograms as a visual reference so we can judge how similar the values in a data set are to a normal distribution.
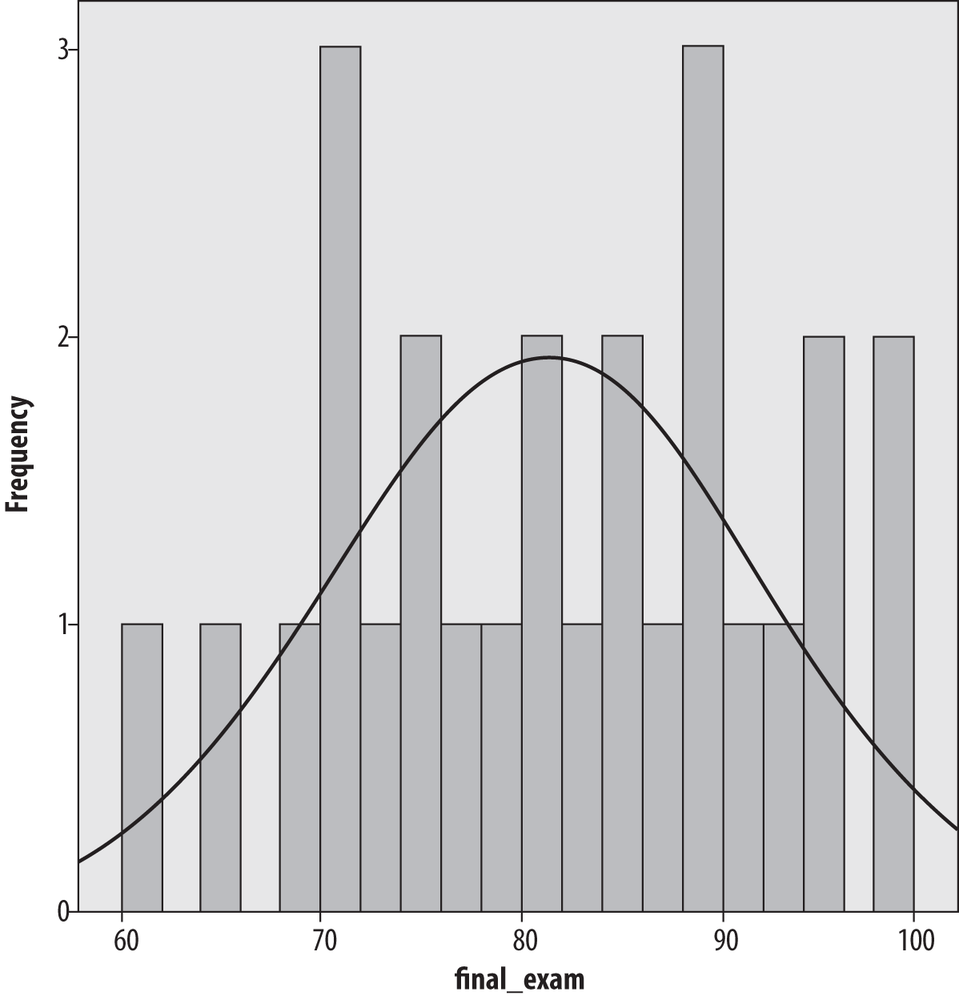
For better or for worse, the choice of the number and width of bars can drastically affect the appearance of the histogram. Usually, histograms have more than four bars; Figure 4-38 shows the same data with eight bars, each with a width of five.
It’s the same data, but it doesn’t look nearly as normal, does it? Figure 4-39 shows the same data with a bin width of two.
It’s clear that the selection of bin width is important to the histogram’s appearance, but how do you decide how many bins to use? This question has been explored in mathematical detail without producing any absolute answers. (If you’re up for a very technical discussion, see the Wand article listed in Appendix C.). There is no absolute answer to this question, but there are some rules of thumb. First, the bins need to encompass the full range of data values. Beyond that, one common rule of thumb is that the number of bins should equal the square root of the number of points in the data set. Another is that the number of bins should never be fewer than about six. These rules clearly conflict in our data set because √26 = 5.1, which is less than 6, so common sense also comes into play, as does trying different numbers of bins and bin widths. If the choice drastically changes the appearance of the data, further investigation is in order.
Charts that display information about the relationship between two variables are called bivariate charts: the most common example is the scatterplot. Scatterplots define each point in a data set by two values, commonly referred to as x and y, and plot each point on a pair of axes; this method should be familiar if you ever worked with Cartesian coordinates in math class. Conventionally the vertical axis is called the y-axis and represents the y-value for each point. The horizontal axis is called the x-axis and represents the x-value. Scatterplots are a very important tool for examining bivariate relationships among variables, a topic further discussed in Chapter 7.
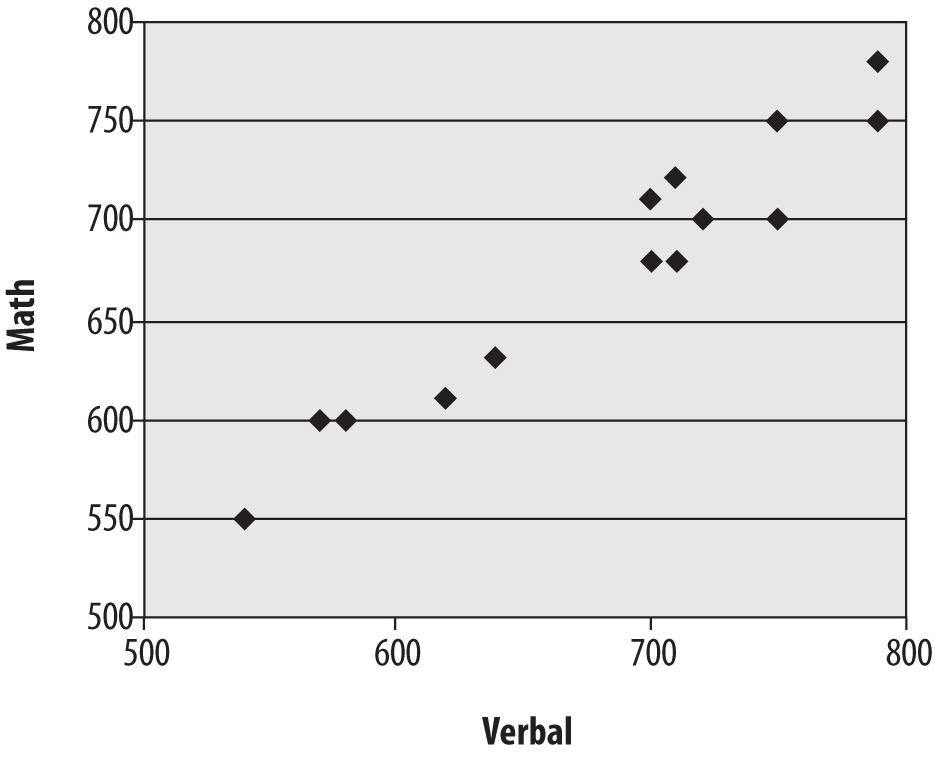
Consider the data set shown in Figure 4-40, which consists of the verbal and math SAT (Scholastic Aptitude Test) scores for a hypothetical group of 15 students.
Other than the fact that most of these scores are fairly high (the SAT is calibrated so that the median score is 500, and most of these scores are well above that), it’s difficult to discern much of a pattern between the math and verbal scores from the raw data. Sometimes the math score is higher, sometimes the verbal score is higher, and often both are similar. However, creating a scatterplot of the two variables, as in Figure 4-41, with math SAT score on the y-axis (vertical axis) and verbal SAT score on the x-axis (horizontal axis), makes the relationship between scores much clearer.
Despite some small inconsistencies, verbal and math scores have a strong linear relationship. People with high verbal scores tend to have high math scores and vice versa, and those with lower scores in one area tend to have lower scores in the other.
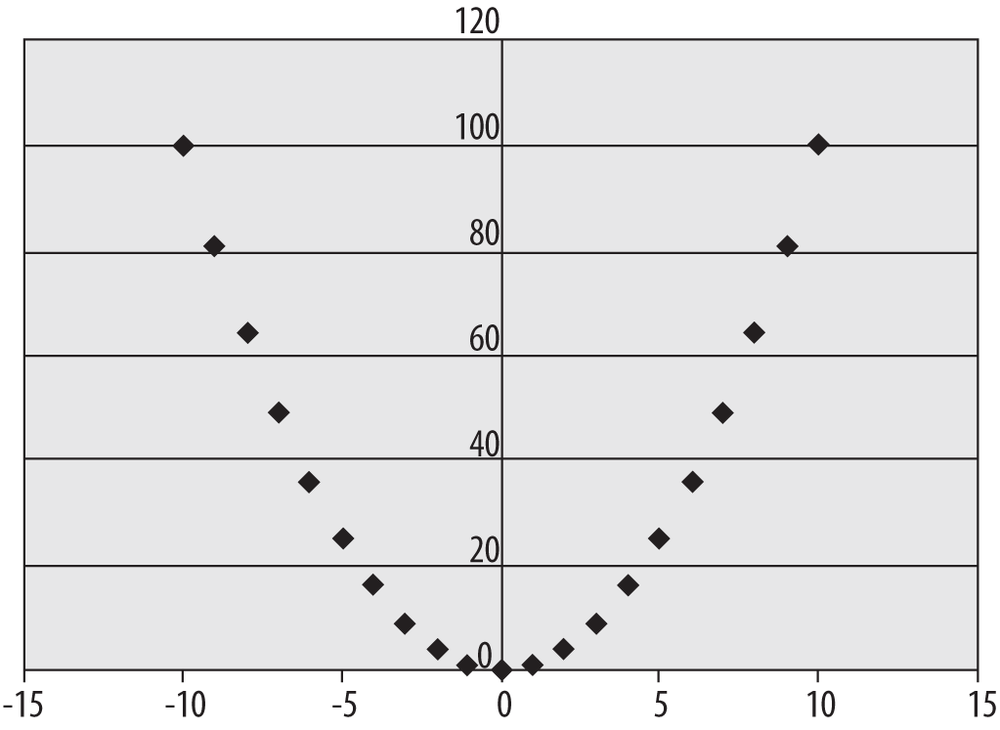
Not all strong relationships between two variables are linear, however. Figure 4-42 shows a scatterplot of variables that are highly related but for which the relationship is quadratic rather than linear.
In the data presented in this scatterplot, the x-values in each pair are the integers from −10 to 10, and the y-values are the squares of the x-values, producing the familiar quadratic plot. Many statistical techniques assume a linear relationship between variables, and it’s hard to see if this is true or not simply by looking at the raw data, so making a scatterplot of all important data pairs is a simple way to check this assumption.
Line graphs are also often used to display the relationship between two variables, usually between time on the x-axis and some other variable on the y-axis. One requirement for a line graph is that there can only be one y-value for each x-value, so it would not be an appropriate choice for data such as the SAT data presented above. Consider the data in Figure 4-43 from the U.S. Centers for Disease Control and Prevention (CDC), showing the percentage of obesity among U.S. adults, measured annually over a 13-year period.
We can see from this table that obesity has been increasing at a steady pace; occasionally, there is a decrease from one year to the next, but more often there is a small increase in the range of 1% to 2%. This information can also be presented as a line chart, as in Figure 4-44, which makes this pattern of steady increase over the years even clearer.
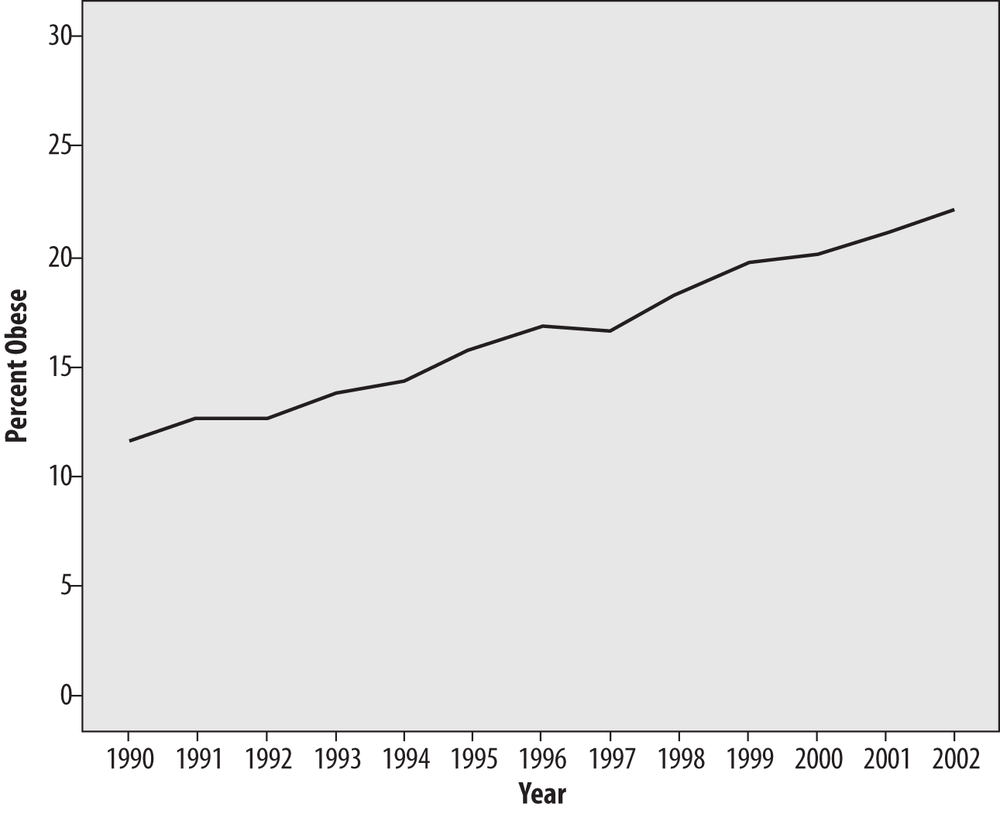
Although this graph represents a straightforward presentation of the data, the visual impact depends partially on the scale and range used for the y-axis (which in this case shows percentage of obesity). Figure 4-44 is a sensible representation of the data, but if we wanted to increase the effect, we could choose a larger scale and smaller range for the y-axis (vertical axis), as in Figure 4-45.
Figure 4-45 presents exactly the same data as Figure 4-44, but a smaller range was chosen for the y-axis (10%–22.5% versus 0%–30%), and the narrower range makes the differences between years look larger. Figure 4-45 is not necessarily an incorrect way to present the data (although many argue that you should also include the 0 point in a graph displaying percent), but it does point out how easy it is to manipulate the appearance of an entirely valid data set. In fact, choosing a misleading range is one of the time-honored ways to “lie with statistics.” (See the sidebar How to Lie with Statistics for more on this topic.)
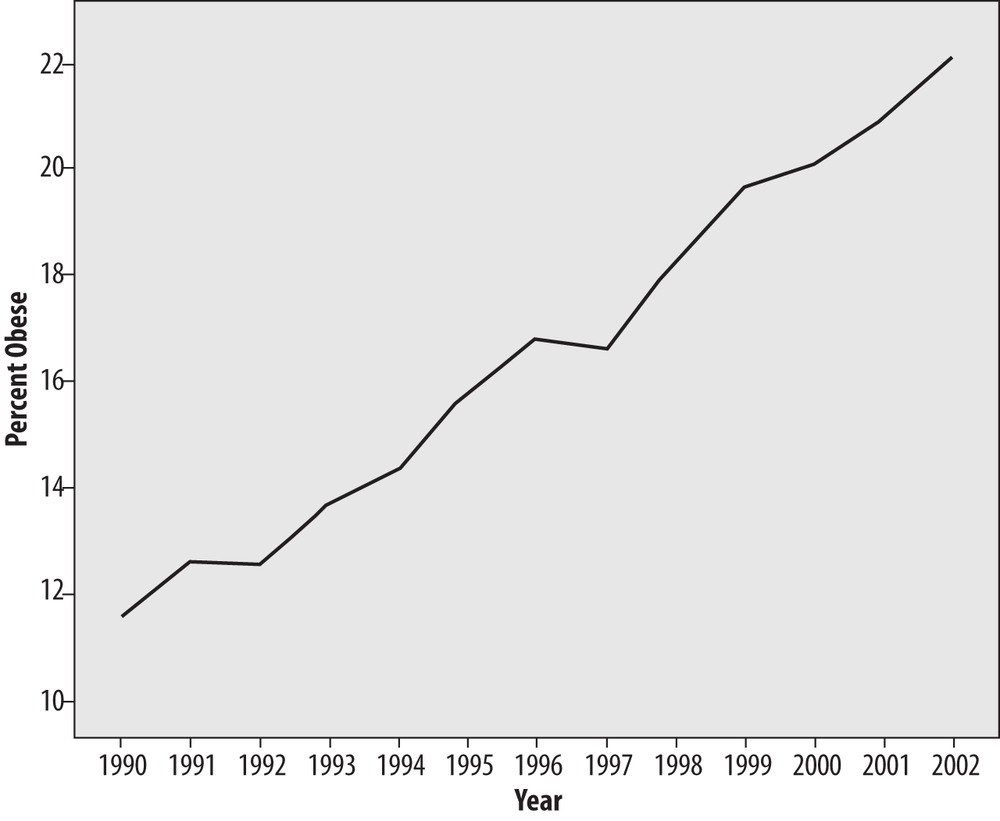
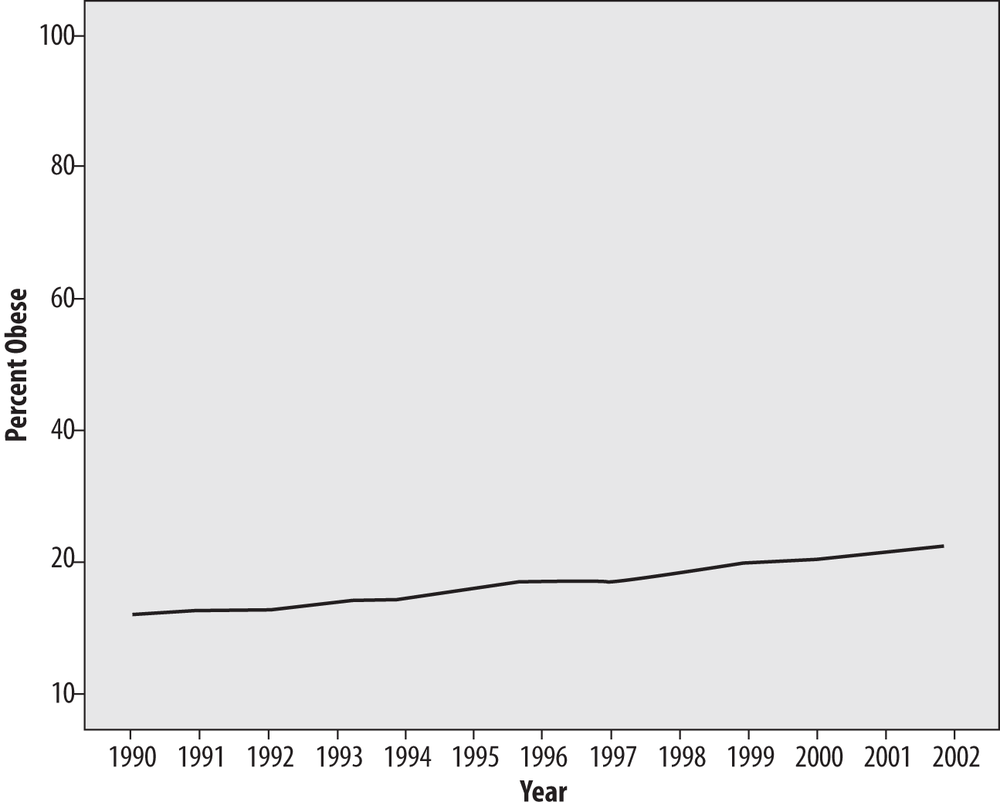
The same trick works in reverse; if we graph the same data by using a wide range for the vertical axis, the changes over the entire period seem much smaller, as in Figure 4-46.
Figure 4-46 presents the same obesity data as Figure 4-44 and Figure 4-45, with a large range on the vertical axis (0%–100%) to decrease the visual impact of the trend.
So which scale should be chosen? There is no perfect answer to this question; all present the same information, and none, strictly speaking, are incorrect. In this case, if I were presenting this chart without reference to any other graphics, the scale would be 7–34 because it shows the true floor for the data (0%, which is the lowest possible value) and includes a reasonable range above the highest data point. Independent of the issues involved with choosing the range for an individual chart, one principle that should be observed if multiple charts are compared to each other (for instance, charts showing the percent obesity in different countries over the same time period or charts of different health risks for the same period), they should all use the same scale to avoid misleading the reader.
Like any other aspect of statistics, learning the techniques of descriptive statistics requires practice. The data sets provided are deliberately simple because if you can apply a technique correctly with 10 cases, you can also apply it with 1,000.
My advice is to try solving the problems several ways, for instance, by hand, using a calculator, and using whatever software is available to you. Even spreadsheet programs such as Microsoft Excel offer many simple mathematical and statistical functions. (Although the usefulness of such functions for serious statistical research is questionable, they might be adequate for initial exploratory work; see the references on Excel in Appendix C for more on this.) In addition, by solving a problem several ways, you will have more confidence that you are using the hardware and software correctly.
Most graphic presentations are created using software, and although each package has good and bad points, most can produce most, if not all, of the graphics presented in this chapter and quite a few other types of graphs as well. The best way to become familiar with graphics is to investigate whatever software you have access to and practice graphing data you currently work with. (If you don’t currently work with data, plenty that you can experiment with is available for free download from the Internet.) Remember that graphic displays are a form of communication, and keep in mind the point you are trying to make with any graphic.
Problem
When is each of the following an appropriate measure of central tendency? Think of some examples for each from your work or studies.
Mean
Median
Mode
Solution
The mean is appropriate for interval or ratio data that is continuous, symmetrical, and lacks significant outliers.
The median is appropriate for continuous data that might be skewed (asymmetrical), based on ranks, or contain extreme values.
The mode is most appropriate for categorical variables or for continuous data sets where one value dominates the others.
Problem
Find some examples of the misleading use of statistical graphics, and explain what the problem is with each.
Solution
This shouldn’t be a difficult task for anyone who follows the news media, but if you get stuck, try searching on the Internet for phrases like “misleading graphics.”
Problem
One of the following data sets could be appropriately displayed as a bar chart and one as a histogram; decide which method is appropriate for each and explain why.
A data set of the heights (in centimeters) of 10,000 entering freshmen at a university
A data set of the majors elected by 10,000 entering freshmen at a university
Solution
The height data would be best displayed as a histogram because these measurements are continuous and have a large number of possible values.
The majors data would be more appropriately displayed as a bar chart because this type of information is categorical and has a restricted set of possible values (although if there is a large number of majors, the less frequent majors might be combined for the sake of clarity).
Problem
One of the following data sets is appropriate for a pie chart, and one is not. Identify which is which, and explain why.
Influenza cases for the past two years, broken down by month
The number of days missed due to the five leading causes for absenteeism at a hospital (the fifth category is “all other,” including all absences attributed to causes other than the first four)
Solution
A pie chart would not be a good choice for the influenza data set because it would have too many categories (24), many of the categories are probably similar in size (because influenza cases are rare in the summer months), and the data doesn’t really reflect parts making up a whole. A better choice might be a bar chart or line chart showing the number of cases by month or season.
The absenteeism data would be a good candidate for a pie chart because there are only five categories, and the parts do add up to 100% of a whole. One question that can’t be answered from this description is whether the different categories (or slices of the pie) are clearly of different size; if so, that would be a further argument in favor of the use of a pie chart.
Problem
What is the median of this data set?
Solution
3. The data set has 9 values, which is an odd number; the median is therefore the middle value when the values are arranged in order. To look at this question more mathematically, because there are n = 9 values, the median is the (n + 1)/2th value; thus, the median is the (9 + 1)/2th or fifth value.
Problem
What is the median of this data set?
Solution
6.5. The data set has 6 values, which is an even number; the median is therefore the average of the middle two values when the values are arranged in order, in this case, 6 and 7. To look at this question more mathematically, the median for an even-numbered set of values is the average of the (n /2)th and (n /2)th + 1 value; n = 6 in this case, so the median is the average of the (6/2)th and (6/2)th + 1 values, that is, the third and fourth values.
Problem
What are the mean and median of the following (admittedly bizarre) data set?
Solution
The mean is ((1 + 7 + 21 + 3 + (−17))/5 = 15/5 = 3.
The median, because there is an odd number of values, is the (n + 1)/2th value, that is, the third value. The data values in order are (−17, 1, 3, 7, 21), so the median is the third value, or 3.
Problem
What are the variance and standard deviation of the following data set? Calculate this by using both the population and sample formulas. Assume µ = 3.
Solution
The population formula to calculate variance is shown in Figure 4-47.
The sample formula is shown in Figure 4-48.
In this case, n = 3, ![]() = 3, and the sum of the squared deviation scores = (−2)2 + 02 + 22 = 8. The population variance is 8/3, or 2.67, and the population standard deviation is the square root of the variance, or 1.63. The sample variance is 8/2, or 4, and the sample standard deviation is the square root of the variance, or 2.
= 3, and the sum of the squared deviation scores = (−2)2 + 02 + 22 = 8. The population variance is 8/3, or 2.67, and the population standard deviation is the square root of the variance, or 1.63. The sample variance is 8/2, or 4, and the sample standard deviation is the square root of the variance, or 2.
Get Statistics in a Nutshell, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.