Think Bayes

Chapter 1. Bayes’s Theorem

Conditional probability

The fundamental idea behind all Bayesian statistics is Bayes’s theorem, which is surprisingly easy to derive, provided that you understand conditional probability. So we’ll start with probability, then conditional probability, then Bayes’s theorem, and on to Bayesian statistics.

A probability is a number between 0 and 1 (including both) that represents a degree of belief in a fact or prediction. The value 1 represents certainty that a fact is true, or that a prediction will come true. The value 0 represents certainty that the fact is false.

Intermediate values represent degrees of certainty. The value 0.5, often written as 50%, means that a predicted outcome is as likely to happen as not. For example, the probability that a tossed coin lands face up is very close to 50%.

A conditional probability is a probability based on some background information. For example, I want to know the probability that I will have a heart attack in the next year. According to the CDC, “Every year about 785,000 Americans have a first coronary attack (http://www.cdc.gov/heartdisease/facts.htm).”

The U.S. population is about 311 million, so the probability that a randomly chosen American will have a heart attack in the next year is roughly 0.3%.

But I am not a randomly chosen American. Epidemiologists have identified many factors that affect the risk of heart attacks; depending on those factors, my risk might be higher or lower than average.

I am male, 45 years old, and I have borderline high cholesterol. Those factors increase my chances. However, I have low blood pressure and I don’t smoke, and those factors decrease my chances.

Plugging everything into the online calculator at http://cvdrisk.nhlbi.nih.gov/calculator.asp, I find that my risk of a heart attack in the next year is about 0.2%, less than the national average. That value is a conditional probability, because it is based on a number of factors that make up my “condition.”

The usual notation for conditional probability is , which is the probability of A given that B is true. In this example, A represents the prediction that I will have a heart attack in the next year, and B is the set of conditions I listed.

Conjoint probability

Conjoint probability is a fancy way to say the probability that two things are true. I write to mean the probability that A and B are both true.

If you learned about probability in the context of coin tosses and dice, you might have learned the following formula:

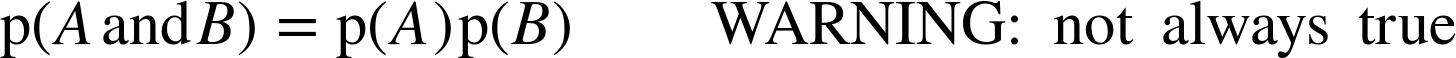
For example, if I toss two coins, and A means the first coin lands face up, and B means the second coin lands face up, then , and sure enough, .

But this formula only works because in this case A and B are independent; that is, knowing the outcome of the first event does not change the probability of the second. Or, more formally, = .

Here is a different example where the events are not independent. Suppose that A means that it rains today and B means that it rains tomorrow. If I know that it rained today, it is more likely that it will rain tomorrow, so .

In general, the probability of a conjunction is

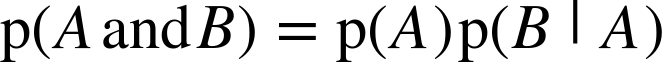
for any A and B. So if the chance of rain on any given day is 0.5, the chance of rain on two consecutive days is not 0.25, but probably a bit higher.

The cookie problem

We’ll get to Bayes’s theorem soon, but I want to motivate it with an example called the cookie problem.¹ Suppose there are two bowls of cookies. Bowl 1 contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each.

Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

This is a conditional probability; we want , but it is not obvious how to compute it. If I asked a different question—the probability of a vanilla cookie given Bowl 1—it would be easy:

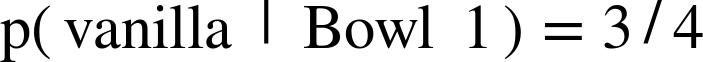
Sadly, is not the same as , but there is a way to get from one to the other: Bayes’s theorem.

Bayes’s theorem

At this point we have everything we need to derive Bayes’s theorem. We’ll start with the observation that conjunction is commutative; that is

for any events A and B.

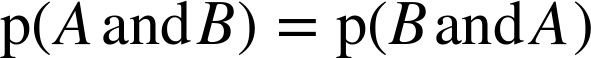
Next, we write the probability of a conjunction:

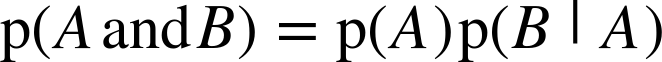
Since we have not said anything about what A and B mean, they are interchangeable. Interchanging them yields

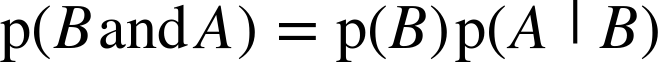
That’s all we need. Pulling those pieces together, we get

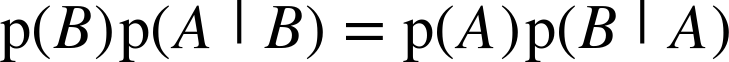
Which means there are two ways to compute the conjunction. If you have , you multiply by the conditional probability . Or you can do it the other way around; if you know , you multiply by . Either way you should get the same thing.

Finally we can divide through by :

And that’s Bayes’s theorem! It might not look like much, but it turns out to be surprisingly powerful.

For example, we can use it to solve the cookie problem. I’ll write B₁ for the hypothesis that the cookie came from Bowl 1 and V for the vanilla cookie. Plugging in Bayes’s theorem we get

The term on the left is what we want: the probability of Bowl 1, given that we chose a vanilla cookie. The terms on the right are:

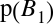• : This is the probability that we chose Bowl 1, unconditioned by what kind of cookie we got. Since the problem says we chose a bowl at random, we can assume .

• : This is the probability of getting a vanilla cookie from Bowl 1, which is 3/4.

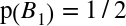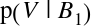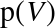• : This is the probability of drawing a vanilla cookie from either bowl. Since we had an equal chance of choosing either bowl and the bowls contain the same number of cookies, we had the same chance of choosing any cookie. Between the two bowls there are 50 vanilla and 30 chocolate cookies, so 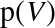= 5/8.

Putting it together, we have

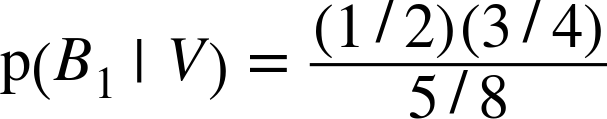
which reduces to 3/5. So the vanilla cookie is evidence in favor of the hypothesis that we chose Bowl 1, because vanilla cookies are more likely to come from Bowl 1.

This example demonstrates one use of Bayes’s theorem: it provides a strategy to get from to . This strategy is useful in cases, like the cookie problem, where it is easier to compute the terms on the right side of Bayes’s theorem than the term on the left.

The diachronic interpretation

There is another way to think of Bayes’s theorem: it gives us a way to update the probability of a hypothesis, H, in light of some body of data, D.

This way of thinking about Bayes’s theorem is called the diachronic interpretation. “Diachronic” means that something is happening over time; in this case the probability of the hypotheses changes, over time, as we see new data.

Rewriting Bayes’s theorem with H and D yields:

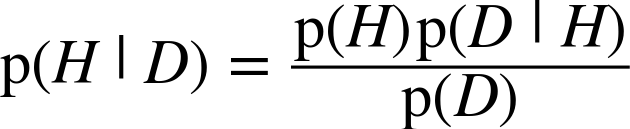
In this interpretation, each term has a name:

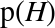• is the probability of the hypothesis before we see the data, called the prior probability, or just prior.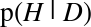

• is what we want to compute, the probability of the hypothesis after we see the data, called the posterior.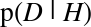

• is the probability of the data under the hypothesis, called the likelihood.

• is the probability of the data under any hypothesis, called the normalizing constant.

Sometimes we can compute the prior based on background information. For example, the cookie problem specifies that we choose a bowl at random with equal probability.

In other cases the prior is subjective; that is, reasonable people might disagree, either because they use different background information or because they interpret the same information differently.

The likelihood is usually the easiest part to compute. In the cookie problem, if we know which bowl the cookie came from, we find the probability of a vanilla cookie by counting.

The normalizing constant can be tricky. It is supposed to be the probability of seeing the data under any hypothesis at all, but in the most general case it is hard to nail down what that means.

Most often we simplify things by specifying a set of hypotheses that are

Mutually exclusive:

At most one hypothesis in the set can be true, and

Collectively exhaustive:

There are no other possibilities; at least one of the hypotheses has to be true.

I use the word suite for a set of hypotheses that has these properties.

In the cookie problem, there are only two hypotheses—the cookie came from Bowl 1 or Bowl 2—and they are mutually exclusive and collectively exhaustive.

In that case we can compute using the law of total probability, which says that if there are two exclusive ways that something might happen, you can add up the probabilities like this:

Plugging in the values from the cookie problem, we have

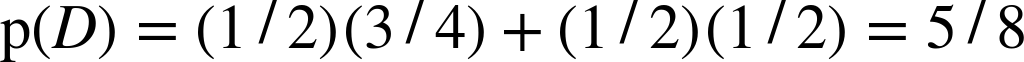
which is what we computed earlier by mentally combining the two bowls.

The M&M problem

M&M’s are small candy-coated chocolates that come in a variety of colors. Mars, Inc., which makes M&M’s, changes the mixture of colors from time to time.

In 1995, they introduced blue M&M’s. Before then, the color mix in a bag of plain M&M’s was 30% Brown, 20% Yellow, 20% Red, 10% Green, 10% Orange, 10% Tan. Afterward it was 24% Blue, 20% Green, 16% Orange, 14% Yellow, 13% Red, 13% Brown.

Suppose a friend of mine has two bags of M&M’s, and he tells me that one is from 1994 and one from 1996. He won’t tell me which is which, but he gives me one M&M from each bag. One is yellow and one is green. What is the probability that the yellow one came from the 1994 bag?

This problem is similar to the cookie problem, with the twist that I draw one sample from each bowl/bag. This problem also gives me a chance to demonstrate the table method, which is useful for solving problems like this on paper. In the next chapter we will solve them computationally.

The first step is to enumerate the hypotheses. The bag the yellow M&M came from I’ll call Bag 1; I’ll call the other Bag 2. So the hypotheses are:

• A: Bag 1 is from 1994, which implies that Bag 2 is from 1996.

• B: Bag 1 is from 1996 and Bag 2 from 1994.

Now we construct a table with a row for each hypothesis and a column for each term in Bayes’s theorem:

	Prior	Likelihood		Posterior
A	1/2	(20)(20)	200	20/27
B	1/2	(10)(14)	70	7/27

The first column has the priors. Based on the statement of the problem, it is reasonable to choose .

The second column has the likelihoods, which follow from the information in the problem. For example, if A is true, the yellow M&M came from the 1994 bag with probability 20%, and the green came from the 1996 bag with probability 20%. Because the selections are independent, we get the conjoint probability by multiplying.

The third column is just the product of the previous two. The sum of this column, 270, is the normalizing constant. To get the last column, which contains the posteriors, we divide the third column by the normalizing constant.

That’s it. Simple, right?

Well, you might be bothered by one detail. I write in terms of percentages, not probabilities, which means it is off by a factor of 10,000. But that cancels out when we divide through by the normalizing constant, so it doesn’t affect the result.

When the set of hypotheses is mutually exclusive and collectively exhaustive, you can multiply the likelihoods by any factor, if it is convenient, as long as you apply the same factor to the entire column.

The Monty Hall problem

The Monty Hall problem might be the most contentious question in the history of probability. The scenario is simple, but the correct answer is so counterintuitive that many people just can’t accept it, and many smart people have embarrassed themselves not just by getting it wrong but by arguing the wrong side, aggressively, in public.

Monty Hall was the original host of the game show Let’s Make a Deal. The Monty Hall problem is based on one of the regular games on the show. If you are on the show, here’s what happens:

• Monty shows you three closed doors and tells you that there is a prize behind each door: one prize is a car, the other two are less valuable prizes like peanut butter and fake finger nails. The prizes are arranged at random.

• The object of the game is to guess which door has the car. If you guess right, you get to keep the car.

• You pick a door, which we will call Door A. We’ll call the other doors B and C.

• Before opening the door you chose, Monty increases the suspense by opening either Door B or C, whichever does not have the car. (If the car is actually behind Door A, Monty can safely open B or C, so he chooses one at random.)

• Then Monty offers you the option to stick with your original choice or switch to the one remaining unopened door.

The question is, should you “stick” or “switch” or does it make no difference?

Most people have the strong intuition that it makes no difference. There are two doors left, they reason, so the chance that the car is behind Door A is 50%.

But that is wrong. In fact, the chance of winning if you stick with Door A is only 1/3; if you switch, your chances are 2/3.

By applying Bayes’s theorem, we can break this problem into simple pieces, and maybe convince ourselves that the correct answer is, in fact, correct.

To start, we should make a careful statement of the data. In this case D consists of two parts: Monty chooses Door B and there is no car there.

Next we define three hypotheses: A, B, and C represent the hypothesis that the car is behind Door A, Door B, or Door C. Again, let’s apply the table method:

	Prior	Likelihood		Posterior
A	1/3	1/2	1/6	1/3
B	1/3	0	0	0
C	1/3	1	1/3	2/3

Filling in the priors is easy because we are told that the prizes are arranged at random, which suggests that the car is equally likely to be behind any door.

Figuring out the likelihoods takes some thought, but with reasonable care we can be confident that we have it right:

• If the car is actually behind A, Monty could safely open Doors B or C. So the probability that he chooses B is 1/2. And since the car is actually behind A, the probability that the car is not behind B is 1.

• If the car is actually behind B, Monty has to open door C, so the probability that he opens door B is 0.

• Finally, if the car is behind Door C, Monty opens B with probability 1 and finds no car there with probability 1.

Now the hard part is over; the rest is just arithmetic. The sum of the third column is 1/2. Dividing through yields and . So you are better off switching.

There are many variations of the Monty Hall problem. One of the strengths of the Bayesian approach is that it generalizes to handle these variations.

For example, suppose that Monty always chooses B if he can, and only chooses C if he has to (because the car is behind B). In that case the revised table is:

	Prior	Likelihood		Posterior
A	1/3	1	1/3	1/2
B	1/3	0	0	0
C	1/3	1	1/3	1/2

The only change is . If the car is behind A, Monty can choose to open B or C. But in this variation he always chooses B, so .

As a result, the likelihoods are the same for A and C, and the posteriors are the same: . In this case, the fact that Monty chose B reveals no information about the location of the car, so it doesn’t matter whether the contestant sticks or switches.

On the other hand, if he had opened C, we would know .

I included the Monty Hall problem in this chapter because I think it is fun, and because Bayes’s theorem makes the complexity of the problem a little more manageable. But it is not a typical use of Bayes’s theorem, so if you found it confusing, don’t worry!

Discussion

For many problems involving conditional probability, Bayes’s theorem provides a divide-and-conquer strategy. If is hard to compute, or hard to measure experimentally, check whether it might be easier to compute the other terms in Bayes’s theorem, , and .

If the Monty Hall problem is your idea of fun, I have collected a number of similar problems in an article called “All your Bayes are belong to us,” which you can read at http://allendowney.blogspot.com/2011/10/all-your-bayes-are-belong-to-us.html.

¹ Based on an example from http://en.wikipedia.org/wiki/Bayes’_theorem that is no longer there.