Think DSP

Chapter 10. LTI Systems

This chapter presents the theory of signals and systems, using musical acoustics as an example. It explains an important application of the Convolution Theorem, characterization of linear, time-invariant systems (which I’ll define soon).

The code for this chapter is in chap10.ipynb, which is in the repository for this book (see “Using the Code”). You can also view it at http://tinyurl.com/thinkdsp10.

Signals and Systems

In the context of signal processing, a system is an abstract representation of anything that takes a signal as input and produces a signal as output.

For example, an electronic amplifier is a circuit that takes an electrical signal as input and produces a (louder) signal as output.

As another example, when you listen to a musical performance, you can think of the room as a system that takes the sound of the performance at the location where it is generated and produces a somewhat different sound at the location where you hear it.

A linear, time-invariant system¹ is a system with these two properties:

Linearity

If you put two inputs into the system at the same time, the result is the sum of their outputs. Mathematically, if an input x₁ produces output y₁ and another input x₂ produces y₂, then 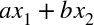produces 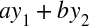, where a and b are scalars.

Time invariance

The ...