Chapter 11. Regression
The linear least squares fit in the previous chapter is an example of regression, which is the more general problem of fitting any kind of model to any kind of data. This use of the term “regression” is a historical accident; it is only indirectly related to the original meaning of the word.
The goal of regression analysis is to describe the relationship between one set of variables, called the dependent variables, and another set of variables, called independent or explanatory variables.
In the previous chapter we used mother’s age as an explanatory variable to predict birth weight as a dependent variable. When there is only one dependent and one explanatory variable, that’s simple regression. In this chapter, we move on to multiple regression, with more than one explanatory variable. If there is more than one dependent variable, that’s multivariate regression.
If the relationship between the dependent and explanatory variable is linear, that’s linear regression. For example, if the dependent variable is y and the explanatory variables are x1 and x2, we would write the following linear regression model:
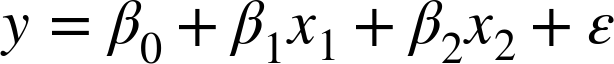
where β0 is the intercept, β1 is the parameter associated with x1, β2 is the parameter associated with x2, and ε is the residual due to random variation or other unknown factors.
Given a sequence of values for y and sequences for x1 and x2, we can find the parameters, ...
Get Think Stats, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

