Type Inheritance and Relational Theory

Chapter 17

Tuple/Relation Values with Inheritance

Everything exists, nothing has value

—E. M. Forster: A Passage to India (1924)

Consider the following tuple types:

TUPLE { E ELLIPSE , R RECTANGLE }     /* "tuple type ER" */TUPLE { E CIRCLE , R RECTANGLE  }     /* "tuple type CR" */TUPLE { E ELLIPSE , R SQUARE    }     /* "tuple type ES" */TUPLE { E CIRCLE , R SQUARE     }     /* "tuple type CS" */

Note the informal names (“tuple type ER,” etc.) for these types as given in the comments. Now, observing with reference to the running example from Part II of this book that CIRCLE and SQUARE are subtypes of ELLIPSE and RECTANGLE, respectively, it should be clear that every tuple of type CS is also a tuple of both type CR and type ES, and further that every tuple of type CR or type ES is also a tuple of type ER. Thus, it should also be clear that tuple type CS is a subtype of both tuple type CR and tuple type ES, and further that tuple types CR and ES are both subtypes of tuple type ER. In other words, subtype / supertype relationships hold as indicated in Fig. 17.1 below.

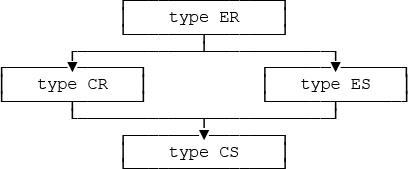
Fig. 17.1: A type graph involving tuple or relation types

Here are some further points arising in connection with this example that should be clear as well but in any case are worth spelling out explicitly:

• All four tuple types have the same attribute names.

• Each of the four tuple types overlaps (i.e., has values in ...