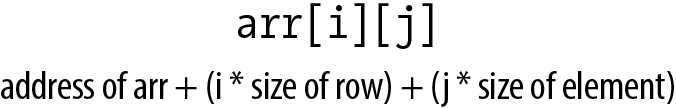Understanding and Using C Pointers

Chapter 4. Pointers and Arrays

An array is a fundamental data structure built into C. A thorough understanding of arrays and their use is necessary to develop effective applications. Misunderstandings of array and pointer usage can result in hard-to-find errors and less than optimal performance in applications. Array and pointer notations are closely related to each other and can frequently be used interchangeably in the right context.

A common misconception is that an array and a pointer are completely interchangeable. An array name is not a pointer. Although an array name can be treated as a pointer at times, and array notation can be used with pointers, they are distinct and cannot always be used in place of each other. Understanding this difference will help you avoid incorrect use of these notations. For example, although the name of an array used by itself will return the array’s address, we cannot use the name by itself as the target of an assignment.

Arrays support many parts of an application and can be single or multidimensional. In this chapter, we will address the fundamental aspects of arrays as they relate to pointers to provide you with a deep understanding of arrays and the various ways they can be manipulated with pointers. You will see their use in more advanced contexts throughout the book.

We start with a quick review of arrays and then examine the similarities and differences between array and pointer notation. Arrays can be created using malloc type functions. These functions provide more flexibility than that afforded by traditional array declarations. We will see how the realloc function can be used to change the amount of memory allocated for an array.

Dynamically allocating memory for an array can present challenges, especially when we are dealing with arrays with two or more dimensions, as we have to ensure that the array is allocated in contiguous memory.

We will also explore problems that can occur when passing and returning arrays. In most situations, the array’s size must be passed so the array can be properly handled in a function. There is nothing inherent in an array’s internal representation that determines its length. If we do not pass the length, the function has no standard means of knowing where the array ends. We will also examine how to create jagged arrays in C, although they are infrequently used. A jagged array is a two-dimensional array where each row may have a different number of columns.

To demonstrate these concepts, we will use a vector for single-dimensional arrays and a matrix for two-dimensional arrays. Vectors and matrices have found extensive use in many areas, including analyzing electromagnetic fields, weather prediction, and in mathematics.

Quick Review of Arrays

An array is a contiguous collection of homogeneous elements that can be accessed using an index. By contiguous, we mean the elements of the array are adjacent to one another in memory with no gaps between them. By homogeneous, we mean they are all of the same type. Array declarations use a set of brackets and can possess multiple dimensions.

Two-dimensional arrays are common, and we typically use the terms rows and columns to describe the position of an array’s element. Arrays with three or more dimensions are not as common but can be quite useful in some applications. A two-dimensional array is not to be confused with an array of pointers. They are similar but behave slightly differently, as will be shown in the sectionUsing a One-Dimensional Array of Pointers.

Variable length arrays were introduced in C99 version of C. Previously, techniques using the realloc function were used to support arrays whose sizes change. We illustrate the realloc function in the section Using the realloc Function to Resize an Array.

Note

Arrays have a fixed size. When we declare an array, we need to decide how big it should be. If we specify too many elements, we waste space. If we specify too few elements, we limit how many elements we can process. The realloc function and variable length arrays provide techniques for dealing with arrays whose size needs to change. With a little work, we can resize an array and use just the right amount of memory.

One-Dimensional Arrays

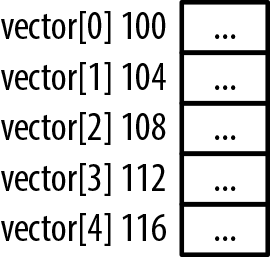
A one-dimensional array is a linear structure. It uses a single index to access its members. The following is a declaration of a five-element array of integers:

   int vector[5];

Array indexes start with 0 and end at one less than their declared size. Valid indexes for the array vector start at 0 and end at 4. However, C does not enforce these bounds. Using an invalid index for an array can result in unpredictable behavior. Figure 4-1 illustrates how the array is allocated in memory. Each element is four bytes in length and is uninitialized. Depending on the memory model used, as explained in Memory Models, the size may be different.

Figure 4-1. Array memory allocation

The internal representation of an array has no information about the number of elements it contains. The array name simply references a block of memory. Using the sizeof operator with an array will return the number of bytes allocated to the array. To determine the number of elements, we divide the array’s size by its element’s size, as illustrated below. This will display 5:

    printf("%d\n", sizeof(vector)/sizeof(int));

One-dimensional arrays can be readily initialized using a block type statement. In the following sequence, each element is initialized to an integer starting at one:

    int vector[5] = {1, 2, 3, 4, 5};

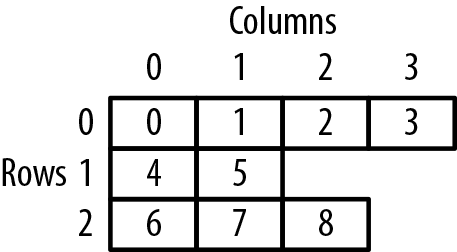
Two-Dimensional Arrays

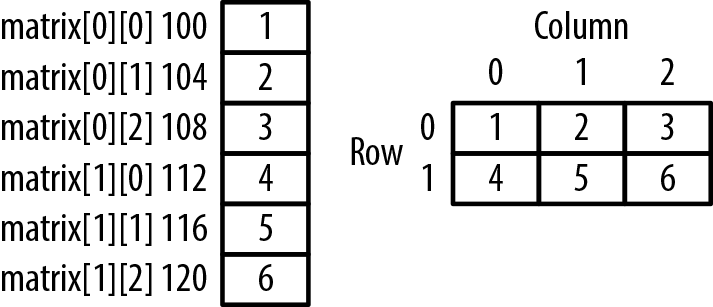
Two-dimensional arrays use rows and columns to identify array elements. This type of array needs to be mapped to the one-dimension address space of main memory. In C this is achieved by using a row-column ordering sequence. The array’s first row is placed in memory followed by the second row, then the third row, and this ordering continues until the last row is placed in memory.

The following declares a two-dimensional array with two rows and three columns. The array is initialized using a block statement. Figure 4-2 illustrates how memory is allocated for this array. The diagram on the left shows how memory is mapped. The diagram on the right shows how it can be viewed conceptually:

    int matrix[2][3] = {{1,2,3},{4,5,6}};

Figure 4-2. Two-dimensional array

A two-dimensional array is treated as an array of arrays. That is, when we access the array using only one subscript, we get a pointer to the corresponding row. This is demonstrated in the following code sequence where each row’s address and size is displayed:

    for (int i = 0; i < 2; i++) {
        printf("&matrix[%d]: %p  sizeof(matrix[%d]): %d\n", 
                i, &matrix[i], i, sizeof(matrix[i]));
    }

The following output assumes the array is located at address 100. The size is 12 because each row has three elements of four bytes each:

&matrix[0]: 100 sizeof(matrix[0]): 12
&matrix[1]: 112 sizeof(matrix[1]): 12

In the section Pointers and Multidimensional Arrays, we will examine this behavior in more detail.

Multidimensional Arrays

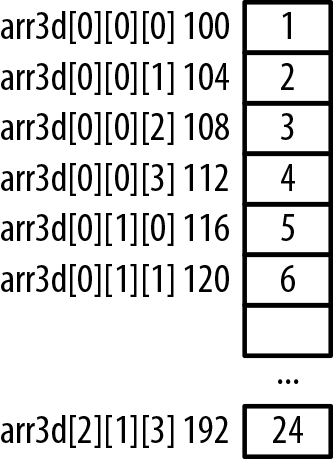
Multidimensional arrays have two or more dimensions. As with two-dimensional arrays, multiple sets of brackets define the array’s type and size. In the following example, we define a three-dimensional array consisting of three rows, two columns, and a rank of four. The term rank is often used to denote the elements of the third dimension:

    int arr3d[3][2][4] = {
        {{1, 2, 3, 4}, {5, 6, 7, 8}},
        {{9, 10, 11, 12}, {13, 14, 15, 16}},
        {{17, 18, 19, 20}, {21, 22, 23, 24}}
    };

The elements are allocated contiguously in row-column-rank order as illustrated in Figure 4-3.

Figure 4-3. Three-dimensional array

We will use these declarations in later examples.

Pointer Notation and Arrays

Pointers can be very useful when working with arrays. We can use them with existing arrays or to allocate memory from the heap and then treat the memory as if it were an array. Array notation and pointer notation can be used somewhat interchangeably. However, they are not exactly the same as detailed in the section Differences Between Arrays and Pointers.

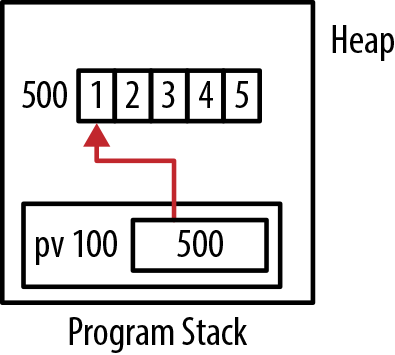
When an array name is used by itself, the array’s address is returned. We can assign this address to a pointer as illustrated below:

    int vector[5] = {1, 2, 3, 4, 5};
    int *pv = vector;

The variable pv is a pointer to the first element of the array and not the array itself. When we first assigned a value to pv, we assigned the address of the array’s first element.

We can use either the array name by itself or use the address-of operator with the array’s first element as illustrated below. These are equivalent and will return the address of vector. Using the address-of operator is more verbose but also more explicit:

    printf("%p\n",vector);
    printf("%p\n",&vector[0]);

The expression &vector is sometimes used to obtain the address of an array. It differs from the other notations in that it returns a pointer to the entire array. The other two approaches yield a pointer to an integer. Instead of returning a pointer to an integer, it returns a pointer to an array of integers. The use of this type will be illustrated in the section Passing a Multidimensional Array.

We can also use array subscripts with pointers. Effectively, the notation pv[i] is evaluated as:

   *(pv + i)

The pointer pv contains the address of a block of memory. The bracket notation will take the address contained in pv and adds the value contained in the index i using pointer arithmetic. This new address is then dereferenced to return its contents.

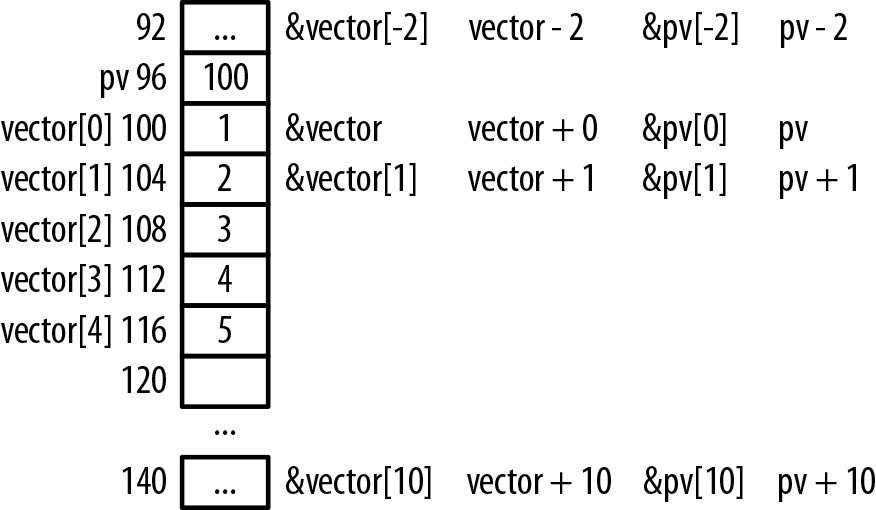
As we discussed in the section Pointer Arithmetic, adding an integer to a pointer will increment the address it holds by the product of the integer and the data type’s size. The same is true if we add an integer to the name of an array. The following two statements are equivalent:

   *(pv + i)
   *(vector + i)

Assume the vector is located at address 100 and pv is located at address 96. Table 4-1 and Figure 4-4 illustrate the use of array subscripts and pointer arithmetic with both the array name and the pointer for various values.

Table 4-1. Array/pointer notation

Value	Equivalent Expression
92	&vector[-2]	vector - 2	&pv[-2]	pv - 2
100	vector	vector+0	&pv[0]	pv
100	&vector[0]	vector+0	&pv[0]	pv
104	&vector[1]	vector + 1	&pv[1]	pv + 1
140	&vector[10]	vector + 10	&pv[10]	pv + 10

Figure 4-4. Array/pointer notation

When we add 1 to the array address we effectively add 4, the size of an integer, to the address since this is an array of integers. With the first and last operations, we addressed locations outside the array’s bounds. While this is not a good practice, it does emphasize the need to be careful when using indexes or pointers to access elements of an array.

Array notation can be thought of as a “shift and dereference” operation. The expression vector[2] means start with vector, which is a pointer to the beginning of the array, shift two positions to the right, and then dereference that location to fetch its value. Using the address-of operator in conjunction with array notation, as in &vector[2], essentially cancels out the dereferencing. It can be interpreted as go left two positions and then return that address.

The following demonstrates the use of pointers in the implementation of the scalar addition operation. This operation takes a value and multiplies it against each element of the vector:

    pv = vector;
    int value = 3;
    for(int i=0; i<5; i++) {
        *pv++ *= value;
    }

Differences Between Arrays and Pointers

There are several differences between the use of arrays and the use of pointers to arrays. In this section, we will use the vector array and pv pointer as defined below:

    int vector[5] = {1, 2, 3, 4, 5};
    int *pv = vector;

The code generated by vector[i] is different from the code generated by vector+i. The notation vector[i] generates machine code that starts at location vector, moves i positions from this location, and uses its content. The notation vector+i generates machine code that starts at location vector, adds i to the address, and then uses the contents at that address. While the result is the same, the generated machine code is different. This difference is rarely of significance to most programmers.

There is a difference when the sizeof operator is applied to an array and to a pointer to the same array. Applying the sizeof operator to vector will return 20, the number of bytes allocated to the array. Applying the sizeof operator against pv will return 4, the pointer’s size.

The pointer pv is an lvalue. An lvalue denotes the term used on the lefthand side of an assignment operator. An lvalue must be capable of being modified. An array name such as vector is not an lvalue and cannot be modified. The address assigned to an array cannot be changed . A pointer can be assigned a new value and reference a different section of memory.

Consider the following:

    pv = pv + 1;
    vector = vector + 1; // Syntax error

We cannot modify vector, only its contents. However, the expression vector+1 is fine, as demonstrated below:

    pv = vector + 1;

Using malloc to Create a One-Dimensional Array

If we allocate memory from the heap and assign the address to a pointer, there is no reason we cannot use array subscripts with the pointer and treat this memory as an array. In the following sequence, we duplicate the contents of the vector array used earlier:

    int *pv = (int*) malloc(5 * sizeof(int));
    for(int i=0; i<5; i++) {
        pv[i] = i+1;
    }

We could have used pointer notation as shown below; however, the array notation is often easier to follow:

    for(int i=0; i<5; i++) {
        *(pv+i) = i+1;
    }

Figure 4-5 illustrates how memory is allocated for this example.

Figure 4-5. Array allocated from the heap

This technique creates a region of memory and treats it as an array. Its size is determined at runtime. However, we need to remember to deallocate the memory when we are through with it.

Warning

In the previous example we used *(pv+i) instead of *pv+1. Since the dereference operator has higher precedence than the plus operator, the second expression’s pointer is dereferenced, giving us the value referenced by the pointer. We then add i to this integer value. This was not what was intended. In addition, when we use this expression as an lvalue, the compiler will complain. Thus, we need to force the addition to be performed first, followed by the dereference operation, in order for it to work correctly.

Using the realloc Function to Resize an Array

We can resize an existing array created using malloc with the realloc function. The essentials of the realloc function were detailed in Chapter 2. The C standard C99 supports variable length arrays. In some situations, this may prove to be a better solution than using the realloc function. If you are not using C99, then the realloc function will need to be used. Also, variable length arrays can only be declared as a member of a function. If the array is needed longer than the function’s duration, then realloc will need to be used.

To illustrate the realloc function, we will implement a function to read in characters from standard input and assign them to a buffer. The buffer will contain all of the characters read in except for a terminating return character. Since we do not know how many characters the user will input, we do not know how long the buffer should be. We will use the realloc function to allocate additional space by a fixed increment amount. The code to implement this function is shown below:

char* getLine(void) {
    const size_t sizeIncrement = 10;
    char* buffer = malloc(sizeIncrement);
    char* currentPosition = buffer;
    size_t maximumLength = sizeIncrement;
    size_t length = 0;    
    int character;

    if(currentPosition == NULL) { return NULL; }

    while(1) {
        character = fgetc(stdin);
        if(character == '\n') { break; }

        if(++length >= maximumLength) {
            char *newBuffer = realloc(buffer, maximumLength += sizeIncrement);

            if(newBuffer == NULL) {
                free(buffer);
                return NULL;
            }
                        
            currentPosition = newBuffer + (currentPosition - buffer);
            buffer = newBuffer;
        }
        *currentPosition++ = character;
    }
    *currentPosition = '\0';
    return buffer;
}

We will start by defining a series of declarations as summarized in Table 4-2.

Table 4-2. getLine variables

sizeIncrement	The size of the initial buffer and the amount it will be incremented by when the buffer needs to be enlarged
buffer	A pointer to the characters read in
currentPosition	A pointer to the next free position in the buffer
maximumLength	The maximum number of characters that can be safely stored in the buffer
length	The number of characters read in
character	The last character read in

The buffer is created with a size of sizeIncrement. If the malloc function is unable to allocate memory, the first if statement will force the function to return NULL. An infinite loop is entered where the characters are processed one at a time. When the loop exits, a NUL is added to terminate the string and the buffer’s address is returned.

Within the while loop, a character is read in. If it is a carriage return, the loop is exited. Next, the if statement determines whether we have exceeded the buffer’s size. Otherwise, the character is added to the current position within the buffer.

If we have exceeded the buffer’s size, the realloc function creates a new block of memory. This block is sizeIncrement bytes larger than the old one. If it is unable to allocate memory, we free up the existing allocated memory and force the function to return NULL. Otherwise, currentPosition is adjusted to point to the right position within the new buffer and we assign the variable buffer to point to the newly allocated buffer. The realloc function will not necessarily keep your existing memory in place, so you have to use the pointer it returns to figure out where your new, resized memory block is.

The variable newBuffer holds the allocated memory’s address. We needed a separate variable, not buffer, in case the realloc was unable to allocate memory. This allows us to detect and handle the condition.

We did not free buffer if realloc was successful because realloc will copy the original buffer to the new buffer and free up the old buffer. If we had tried to free buffer, then it would normally result in the program’s termination because we tried to free the same block of memory twice.

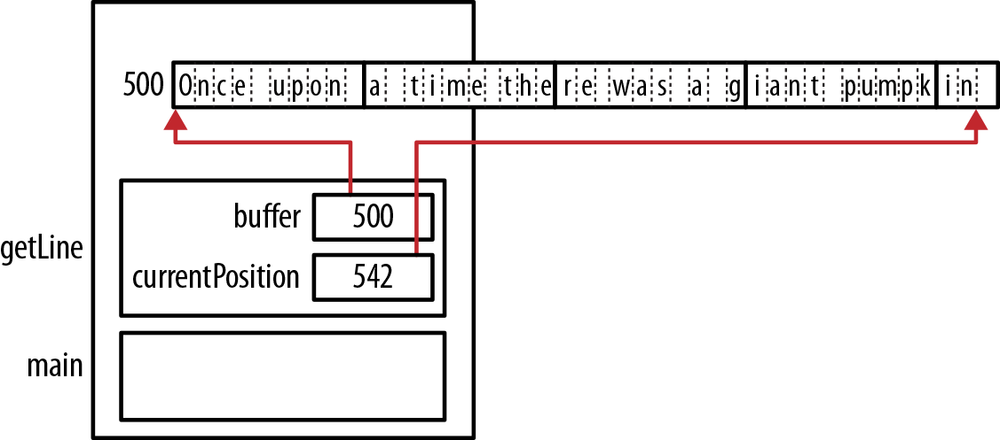
Figure 4-6 illustrates memory being allocated for the getLine function with an input string of “Once upon a time there was a giant pumpkin.” The program stack has been simplified to ignore the local variables except for buffer and currentPosition. The buffer has been extended four times, as indicated by the rectangle containing the input string.

Figure 4-6. Memory allocation for getLine function

The realloc function can also be used to decrease the amount of space used by a pointer. To illustrate its use, the trim function shown below will remove leading blanks in a string:

char* trim(char* phrase) {
    char* old = phrase;
    char* new = phrase;
    
    while(*old == ' ') {
        old++;
    }
    
    while(*old) {
        *(new++) = *(old++);
    }
    *new = 0;
    return (char*) realloc(phrase,strlen(phrase)+1);    
}

int main() {
    char* buffer = (char*)malloc(strlen("  cat")+1);
    strcpy(buffer,"  cat");
    printf("%s\n",trim(buffer));
}

The first while loop uses the tmp variable to skip over any leading blanks. The second while loop copies the remaining characters in the string to the beginning of the string. It will evaluate to true until NUL is reached, which will evaluate to false. A zero is then added to terminate the string. The realloc function is then used to reallocate the memory based on the string’s new length.

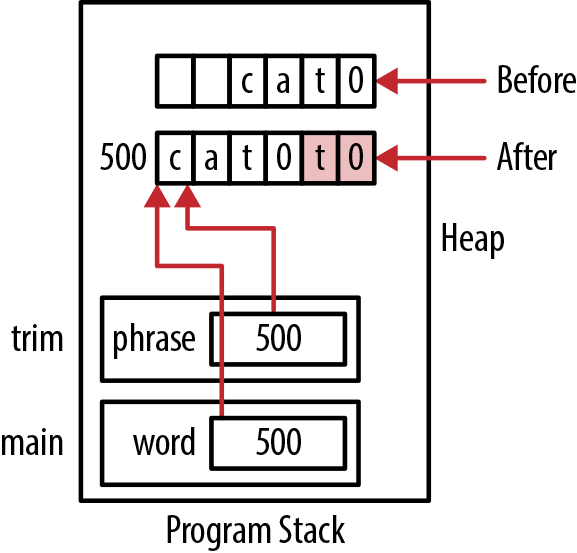
Figure 4-7 illustrates the function’s use with an original string of “cat.” The state of string before and after the trim function executes is shown. The memory in red is the old memory and should not be accessed.

Figure 4-7. Realloc example

Passing a One-Dimensional Array

When a one-dimensional array is passed to a function, the array’s address is passed by value. This makes the transfer of information more efficient since we are not passing the entire array and having to allocate memory in the stack for it. Normally, this means the array’s size must be passed. If we don’t, from the function’s perspective all we have is the address of an array with no indication of its size.

Unless there is something integral to the array to tell us its bounds, we need to pass the size information when we pass the array. In the case of a string stored in an array, we can rely on the NUL termination character to tell us when we can stop processing the array. We will examine this in Chapter 5. Generally, if we do not know the array’s size, we are unable to process its elements and can wind up working with too few elements or treating memory outside of the array as if it were part of the array. This will frequently result in abnormal program termination.

We can declare the array in the function declaration using one of two notations: array notation or pointer notation.

Using Array Notation

In the following example, an integer array is passed to a function along with its size. Its contents are then displayed:

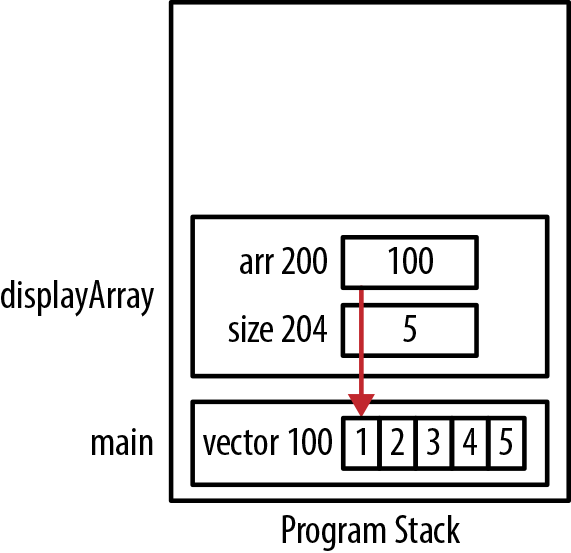
void displayArray(int arr[], int size) {
    for (int i = 0; i < size; i++) {
        printf("%d\n", arr[i]);
    }
}

    int vector[5] = {1, 2, 3, 4, 5};
    displayArray(vector, 5);

The sequence’s output will be the numbers 1 through 5.We passed the number 5 to the function that indicates its size. We could have passed any positive number and the function would attempt to display the corresponding number of elements, regardless of whether the size was correct. The program may terminate if we attempt to address memory outside of the array’s bounds. The memory allocation for this example is shown in Figure 4-8.

Figure 4-8. Using array notation

Warning

A common mistake is to use the sizeof operator with the array in order to determine its number of elements, as shown below. However, as explained in the sectionOne-Dimensional Arrays, this is not the correct way of determining its size. In this case, we would be passing the value of 20 to the array.

    displayArray(arr, sizeof(arr));

It is a common practice to pass a size smaller than the actual number of elements in an array. This is done to process only part of an array. For example, assume we read in a series of ages into an array but did not fill up the array. If we called a sort function to sort it, we would only want to sort the valid ages, not every array element.

Using Pointer Notation

We do not have to use the bracket notation when declaring an array parameter of a function. Instead, we can use pointer notation as follows:

void displayArray(int* arr, int size) {
    for (int i = 0; i < size; i++) {
        printf("%d\n", arr[i]);
    }
}

We continued to use array notation within the function. If desired, we could have used pointer notation in the function:

void displayArray(int* arr, int size) {
    for (int i = 0; i < size; i++) {
        printf("%d\n", *(arr+i));
    }
}

If we had used array notation to declare the function, we could have still used pointer notation in the function’s body:

void displayArray(int arr[], int size) {
    for (int i = 0; i < size; i++) {
        printf("%d\n", *(arr+i));
    }
}

Using a One-Dimensional Array of Pointers

In this section, we will examine the key aspects of using an array of pointers by using an array of pointers to integer. Examples of array of pointers can also be found in:

• Using an Array of Function Pointers, where we use an array of function pointers;

• How Memory Is Allocated for a Structure, where an array of structures is used; and

• Passing Arguments to an Application, where the argv array is handled.

The purpose of this section is to set the stage for later examples by illustrating the essence of the approach. The following sequence declares an array of integer pointers, allocates memory for each element, and initializes this memory to the array’s index:

    int* arr[5];
    for(int i=0; i<5; i++) {
        arr[i] = (int*)malloc(sizeof(int));
        *arr[i] = i;
    }

If this array was displayed, the numbers 0 through 4 would be printed. We used arr[i] to reference the pointer and *arr[i] to assign a value to the location referenced by the pointer. Do not let the use of array notation confuse you. Since arr was declared as an array of pointers, arr[i] returns an address. When we dereference a pointer such as *arr[i], we get the contents at that address.

We could have used the following equivalent pointer notation for the loop’s body:

        *(arr+i) = (int*)malloc(sizeof(int));
        **(arr+i) = i;

This notation is harder to follow, but understanding it will further your C expertise. We are using two levels of indirection in the second statement. Mastery of this type of notation will separate you from the less experienced C programmers.

The subexpression (arr+i) represents the address of the array’s i^th element. We need to modify the content of this address so we use the subexpression *(arr+i). The allocated memory is assigned to this location in the first statement. Dereferencing this subexpression a second time, as we do in the second statement, returns the allocated memory’s location. We then assign the variable i to it. Figure 4-9 illustrates how memory is allocated.

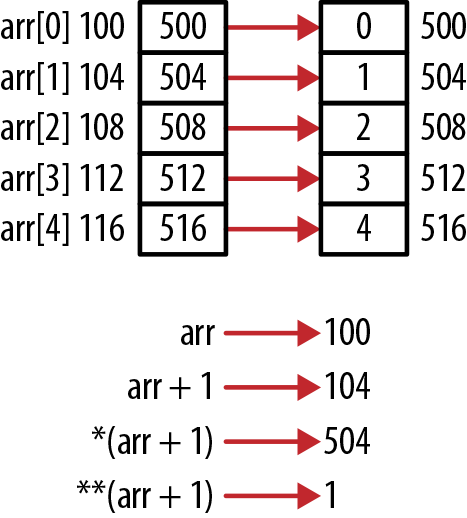
For example, arr[1] is located at address 104. The expression (arr+1) will give us 104. Using *(arr+1) gives us its content. In this example, it is the pointer 504. Dereferencing this a second time using **(arr+1) gives us the contents of 504, which is a 1.

Figure 4-9. Array of pointers

Example expressions are listed in Table 4-3. Reading pointer expression from left to right and not ignoring parentheses can help in understanding how they work.

Table 4-3. Array of pointers expressions

Expression	Value
*arr[0]	0
**arr	0
**(arr+1)	1
arr[0][0]	0
arr[3][0]	3

The first three expressions are similar to those in the previous explanation. The last two are different. The use of a pointer to a pointer notation suggests we are dealing with an array of pointers. In effect, this is what we are doing. If we reexamine Figure 4-9 and pretend each element of arr points to an array of size one, then the last two expressions make sense. What we have is a five-element array of pointers to a series of one-element arrays.

The expression arr[3][0] refers to the fourth element of arr and then the first element of the array it points to. The expression arr[3][1] does not work because the array the fourth element is pointing to does not have two elements.

This suggests the ability to create jagged arrays. This is indeed possible and is the subject of the sectionJagged Arrays and Pointers.

Pointers and Multidimensional Arrays

Parts of multidimensional arrays can be treated as subarrays. For example, each row of a two-dimensional array can be treated as a one-dimensional array. This behavior affects how we use pointers when dealing with multidimensional arrays.

To illustrate this behavior, we create a two-dimensional array and initialize it as follows:

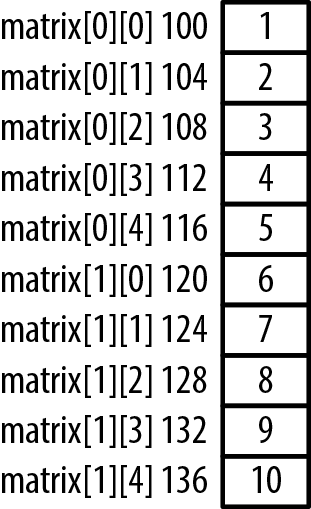
   int matrix[2][5] = {{1,2,3,4,5},{6,7,8,9,10}};

The addresses and their corresponding values are then displayed:

   for(int i=0; i<2; i++) {
      for(int j=0; j<5; j++) {
         printf("matrix[%d][%d]  Address: %p  Value: %d\n",
                    i, j, &matrix[i][j], matrix[i][j]);
      }
   }

The output follows:

matrix[0][0]  Address: 100  Value: 1
matrix[0][1]  Address: 104  Value: 2
matrix[0][2]  Address: 108  Value: 3
matrix[0][3]  Address: 112  Value: 4
matrix[0][4]  Address: 116  Value: 5
matrix[1][0]  Address: 120  Value: 6
matrix[1][1]  Address: 124  Value: 7
matrix[1][2]  Address: 128  Value: 8
matrix[1][3]  Address: 132  Value: 9
matrix[1][4]  Address: 136  Value: 10

The array is stored in row-column order. That is, the first row is stored sequentially in memory followed by the second row. The memory allocation is illustrated in Figure 4-10.

We can declare a pointer for use with this array as follows:

   int (*pmatrix)[5] = matrix;

Figure 4-10. Two-dimensional array memory allocation

The expression, (*pmatrix), declares a pointer to an array. Combined with the rest of the declaration, pmatrix is defined as a pointer to a two-dimensional array of integers with five elements per column. If we had left the parentheses off, we would have declared a five-element array of pointers to integers. The size of the first dimension is 2 since we know the dimensions of the matrix. If a different size is used to access the array, then the results are unpredictable.

If we want to access the second element, 2, using pointer notation, it might seem reasonable to use the following:

    printf("%p\n", matrix);
    printf("%p\n", matrix + 1);

The output follows:

100
120

The address returned by matrix+1 is not offset by 4 from the beginning of the array. Instead, it is offset by the first row’s size, 20 bytes. Using matrix by itself returns the address of the array’s first element. Since a two-dimensional array is an array of arrays, we get the address of a five-element integer array. Its size is 20. We can verify this with the following statement, which will display 20:

    printf("%d\n",sizeof(matrix[0]));  // Displays 20

To access the array’s second element, we need to add 1 to the first row of the array as follows: *(matrix[0] + 1). The expression, matrix[0], returns the address of the first element of the first row of the array. This address is the address of an array of integers. Thus, when we add one to it, the size of a single integer is added to it, giving us the second element. The output will be 104 and 2.

   printf("%p  %d\n", matrix[0] + 1, *(matrix[0] + 1));

We can graphically depict the array as illustrated in Figure 4-11.

Figure 4-11. Graphically depiction of a two-dimensional array

Two-dimensional array notation can be interpreted as shown in Figure 4-12.

Figure 4-12. Two-dimensional array notation

Passing a Multidimensional Array

Passing a multidimensional array to a function can be confusing, especially when pointer notation is used. When passing a multidimensional array, we need to determine whether to use array notation or pointer notation in the function’s signature. Another consideration is how to convey the array’s shape. By shape, we are referring to the number and size of its dimensions. If we want to use array notation within the function, it is imperative to specify the array’s shape. Otherwise, the compiler is unable to use subscripts.

To pass the matrix array, use either:

void display2DArray(int arr[][5], int rows) {

or:

void display2DArray(int (*arr)[5], int rows) {

In both versions the number of columns is specified. This is needed because the compiler needs to know the number of elements in each row. If this information is not passed, then it is unable to evaluate expressions such as arr[0][3] as explained in the section Pointers and Multidimensional Arrays.

In the first version, the expression arr[] is an implicit declaration of a pointer to an array. In the second version, the expression (*arr) is an explicit declaration of the pointer.

Warning

The following declaration will not work correctly:

void display2DArray(int *arr[5], int rows) {

While it will not generate a syntax error, the array passed is assumed to be a five-element array of pointers to integers. Using a One-Dimensional Array of Pointers discusses arrays of pointers.

A simple implementation of this function and invocation follows:

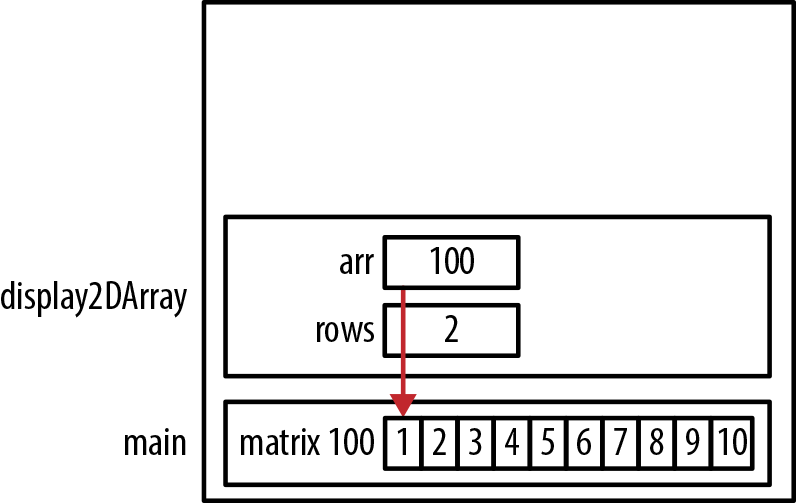
void display2DArray(int arr[][5], int rows) {
    for (int i = 0; i<rows; i++) {
        for (int j = 0; j<5; j++) {
            printf("%d", arr[i][j]);
        }
        printf("\n");
    }
}

void main() {
    int matrix[2][5] = {
        {1, 2, 3, 4, 5},
        {6, 7, 8, 9, 10}
    };
    display2DArray(matrix, 2);
}

The function does not allocate memory for the array. Only the address is passed. The program stack’s state for this call is shown in Figure 4-13.

Figure 4-13. Passing multidimensional array

You may encounter a function declared as follows. It is passed a single pointer and the number of rows and columns:

void display2DArrayUnknownSize(int *arr, int rows, int cols) {
    for(int i=0; i<rows; i++) {
        for(int j=0; j<cols; j++) {
            printf("%d ", *(arr + (i*cols) + j));
        }
        printf("\n");
    }
}

The printf statement calculates the address of each element by adding to arr the number of elements in the previous row(s), (i*cols), and then adding j to specify the column. To invoke the function, we can use the following:

    display2DArrayUnknownSize(&matrix[0][0], 2, 5);

Within the function, we cannot use array subscripts as shown below:

    printf("%d ", arr[i][j]);

This is not possible because the pointer is not declared as a two-dimensional array. However, it is possible to use array notation as shown below. We can use a single subscript since it will be interpreted simply as an offset within the array, whereas two subscripts cannot be used because the compiler doesn’t know the size of the dimensions:

    printf("%d ", (arr+i)[j]);

The first element’s address is passed using &matrix[0][0] instead of matrix. While using matrix will execute correctly, a warning will be generated, indicating incompatible pointer types. The expression &matrix[0][0] is a pointer to an integer, whereas matrix is a pointer to an array of integers.

When passing an array with more than two dimensions, all but the size of the first dimension need to be specified. The following demonstrates a function written to display a three-dimensional array. The last two dimensions are specified in the declaration:

void display3DArray(int (*arr)[2][4], int rows) {
    for(int i=0; i<rows; i++) {
        for(int j=0; j<2; j++) {
            printf("{");
            for(int k=0; k<4; k++) {
                printf("%d ", arr[i][j][k]);
            }
            printf("}");
        }
        printf("\n");
    }
}

The following code shows the function’s invocation:

    int arr3d[3][2][4] = {
        {{1, 2, 3, 4}, {5, 6, 7, 8}},
        {{9, 10, 11, 12}, {13, 14, 15, 16}},
        {{17, 18, 19, 20}, {21, 22, 23, 24}}
    };

    display3DArray(arr3d,3);

The output follows:

{1 2 3 4 }{5 6 7 8 }
{9 10 11 12 }{13 14 15 16 }
{17 18 19 20 }{21 22 23 24 }

Allocation of the array’s memory is depicted in Figure 4-14.

Figure 4-14. Three-dimensional array

The expression arr3d[1] refers to the array’s second row and is a pointer to a two-dimensional array with two rows and four columns. The expression arr3d[1][0] refers to the second row, first column of the array and is a pointer to a one-dimensional array of size 5.

Dynamically Allocating a Two-Dimensional Array

Several issues are involved with dynamically allocating memory for a two-dimensional array, including:

• Whether the array elements need to be contiguous

• Whether the array is jagged

Memory is allocated contiguously when a two-dimensional array is declared as follows:

   int matrix[2][5] = {{1,2,3,4,5},{6,7,8,9,10}};

However, when we use a function such as malloc to create a two-dimensional array, there are variations in how memory can be allocated. Since a two-dimensional array can be treated as an array of arrays, there is no reason the “inner” arrays need to be contiguous. When array subscripts are used with such an array, the array’s noncontiguous nature is handled transparently.

Note

Whether or not it is contiguous can affect other operations, such as copying a block of memory. Multiple copies may be required if the memory is not contiguous.

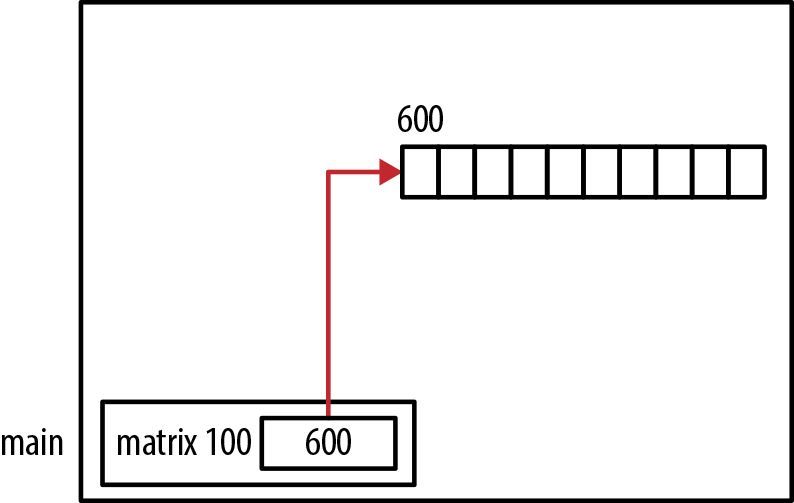
Allocating Potentially Noncontiguous Memory

The following illustrates one way of allocating a two-dimensional array where the allocated memory is not guaranteed to be contiguous. First, the “outer” array is allocated and then each row is allocated using separate malloc statements:

    int rows = 2;
    int columns = 5;
    
    int **matrix = (int **) malloc(rows * sizeof(int *));
    
    for (int i = 0; i < rows; i++) {
        matrix[i] = (int *) malloc(columns * sizeof(int));
    }

Since separate malloc calls were used, the allocated memory is not guaranteed to be contiguous. This is illustrated in Figure 4-15.

Figure 4-15. Noncontiguous allocation

The actual allocation depends on the heap manager and the heap’s state. It may well be contiguous.

Allocating Contiguous Memory

We will present two approaches for allocating contiguous memory for a two-dimensional array. The first technique allocates the “outer” array first and then all of the memory for the rows. The second technique allocates all of the memory at once.

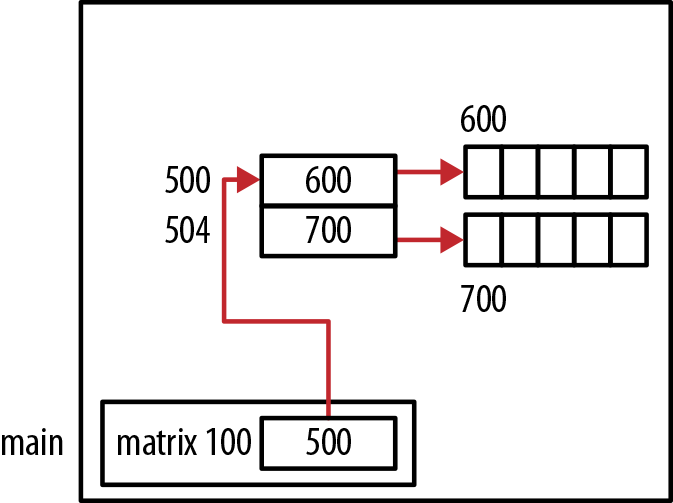
The first technique is illustrated in the following sequence. The first malloc allocates an array of pointers to integers. Each element will be used to hold a pointer to a row. This is the block allocated at address 500 in Figure 4-16. The second malloc allocates memory for all of the elements of the array at location 600. In the for loop, each element of the first array is assigned a portion of the memory allocated by the second malloc:

    int rows = 2;
    int columns = 5;
    int **matrix = (int **) malloc(rows * sizeof(int *));
    matrix[0] = (int *) malloc(rows * columns * sizeof(int));
    for (int i = 1; i < rows; i++)
        matrix[i] = matrix[0] + i * columns;

Figure 4-16. Contiguous allocation with two malloc calls

Technically, the memory for the first array may be separated from the memory for the array’s “body.” However, a contiguous region of memory is allocated for the body.

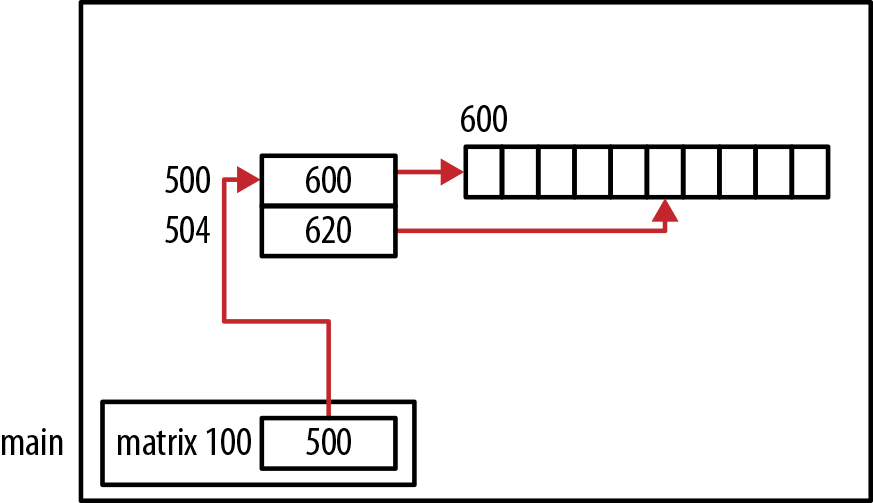
In the second technique shown below, all of the memory for the array is allocated at one time:

    int *matrix = (int *)malloc(rows * columns * sizeof(int));

This allocation is illustrated in Figure 4-17.

Figure 4-17. Contiguous allocation with a single malloc call

When the array is referenced later in code, array subscripts cannot be used. Instead, indexes into the array need to be calculated manually, as illustrated in the following code sequence. Each array element is initialized to the product of its indexes:

    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < columns; j++) {
            *(matrix + (i*columns) + j) = i*j;
        }
    }

Array subscripts cannot be used because we have lost the shape information needed by the compiler to permit subscripts. This concept is explained in the section Passing a Multidimensional Array.

This approach has limited use in the real world, but it does illustrate the relationship between the concept of a two-dimensional array and the one-dimensional nature of main memory. The more convenient two-dimensional array notation makes this mapping transparent and easier to use.

We have demonstrated two general approaches for allocating contiguous memory for a two-dimensional array. The approach to use depends on the needs of the application. However, the last approach generates a single block of memory for the “entire” array.

Jagged Arrays and Pointers

A jagged array is a two-dimensional array possessing a different number of columns for each row. Conceptually, this is illustrated in Figure 4-18, where the array has three rows with a varying number of columns per row.

Figure 4-18. Jagged array

Before we learn how to create such an array, let’s examine a two-dimensional array created using compound literals. A compound literal is a C construct that consists of what appears to be a cast operator followed by an initializer list enclosed in braces. An example of a compound literal follows for both a constant integer and an array of integers. These would be used as part of a declaration:

(const int) {100}
(int[3]) {10, 20, 30}

In the following declaration, we create the array arr1 by declaring it as an array of pointers to an integer and using a block statement of compound literals to initialize it:

    int (*(arr1[])) = {
        (int[]) {0, 1, 2},
        (int[]) {3, 4, 5},
        (int[]) {6, 7, 8}};

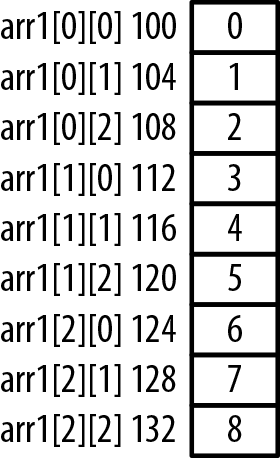
This array has three rows and three columns. The array’s elements are initialized with the value 0 through 8 in row column order. Figure 4-19 depicts how memory is laid out for this array.

Figure 4-19. Two-dimensional array

The following sequence displays the addresses and values of each array element:

    for(int j=0; j<3; j++) {
        for(int i=0; i<3; i++) {
            printf("arr1[%d][%d]  Address: %p  Value: %d\n", 
                    j, i, &arr1[j][i], arr1[j][i]);
        }
        printf("\n");
    }

When executed, we will get the following output:

arr1[0][0]  Address: 0x100  Value: 0
arr1[0][1]  Address: 0x104  Value: 1
arr1[0][2]  Address: 0x108  Value: 2

arr1[1][0]  Address: 0x112  Value: 3
arr1[1][1]  Address: 0x116  Value: 4
arr1[1][2]  Address: 0x120  Value: 5

arr1[2][0]  Address: 0x124  Value: 6
arr1[2][1]  Address: 0x128  Value: 7
arr1[2][2]  Address: 0x132  Value: 8

This declaration can be modified slightly to create a jagged array as depicted in Figure 4-18. The array declaration follows:

    int (*(arr2[])) = {
        (int[]) {0, 1, 2, 3},
        (int[]) {4, 5},
        (int[]) {6, 7, 8}};

We used three compound literals to declare the jagged array. The array’s elements are initialized in row-column order starting with a value of zero. The next sequence will display the array to verify its creation. The sequence required three for loops because each row had a different number of columns:

    int row = 0;
    for(int i=0; i<4; i++) {
        printf("layer1[%d][%d]  Address: %p  Value: %d\n", 
                row, i, &arr2[row][i], arr2[row][i]);
    }
    printf("\n"); 

    row = 1;
    for(int i=0; i<2; i++) {
        printf("layer1[%d][%d]  Address: %p  Value: %d\n", 
                row, i, &arr2[row][i], arr2[row][i]);
    }
    printf("\n");

    row = 2;
    for(int i=0; i<3; i++) {
        printf("layer1[%d][%d]  Address: %p  Value: %d\n", 
                row, i, &arr2[row][i], arr2[row][i]);
    }
    printf("\n");

The output of this sequence follows:

arr2[0][0]  Address: 0x000100  Value: 0
arr2[0][1]  Address: 0x000104  Value: 1
arr2[0][2]  Address: 0x000108  Value: 2
arr2[0][3]  Address: 0x000112  Value: 3

arr2[1][0]  Address: 0x000116  Value: 4
arr2[1][1]  Address: 0x000120  Value: 5

arr2[2][0]  Address: 0x000124  Value: 6
arr2[2][1]  Address: 0x000128  Value: 7
arr2[2][2]  Address: 0x000132  Value: 8

Figure 4-20 depicts how memory is laid out for this array.

Figure 4-20. Jagged array memory allocation

In these examples, we used array notation as opposed to pointer notation when accessing the array’s contents. This made it somewhat easier to see and understand. However, pointer notation would have worked as well.

Compound literals are useful in creating jagged arrays. However, accessing elements of a jagged array can be awkward, as demonstrated with the previous three for loops. This example can be simplified if a separate array is used to maintain the size of each column. While you can create jagged arrays in C, it may not be worth the effort.

Summary

We started with a quick review of arrays and then examined the similarities and differences between array and pointer notation. Arrays can be created using malloc type functions. These type of functions provide more flexibility than afforded by traditional array declaration. We saw how we can use the realloc function to change the amount of memory allocated for an array.

Dynamically allocating memory for an array can present challenges. In the case with two or more dimensional arrays, we have to be careful to make sure the array is allocated in contiguous memory.

We also explored the problems that can occur when passing and returning arrays. Passing the array’s size to a function is normally required so the function can properly handle the array. We also examined how to create jagged arrays in C.