Chapter 4. Just Add Power
In Chapter 3, we investigated finite automata, imaginary machines that strip away the complexity of a real computer and reduce it to its simplest possible form. We explored the behavior of those machines in detail and saw what they’re useful for; we also discovered that, despite having an exotic method of execution, nondeterministic finite automata have no more power than their more conventional deterministic counterparts.
The fact that we can’t make a finite automaton more capable by adding fancy features like nondeterminism and free moves suggests that we’re stuck on a plateau, a level of computational power that’s shared by all these simple machines, and that we can’t break away from that plateau without making more drastic changes to the way the machines work. So how much power do all these machines really have? Well, not much. They’re limited to a very specific application—accepting or rejecting sequences of characters—and even within that small scope, it’s still easy to come up with languages that no machine can recognize.
For example, think about designing a finite state machine capable of reading a string of opening and closing brackets and accepting that string only if the brackets are balanced—that is, if each closing bracket can be paired up with an opening bracket from earlier in the string.[29]
The general strategy for solving this problem is to read characters one at a time while keeping
track of a number that represents the current nesting level: reading an
opening bracket increases the nesting level, and reading a closing bracket decreases it.
Whenever the nesting level is zero, we know that the brackets we’ve read so far are
balanced—because the nesting level has gone up and come down by exactly the same amount—and if
we try to decrease the nesting level below zero, then we know we’ve seen too many closing
brackets (e.g., '())') and that the string must be
unbalanced, no matter what its remaining characters are.
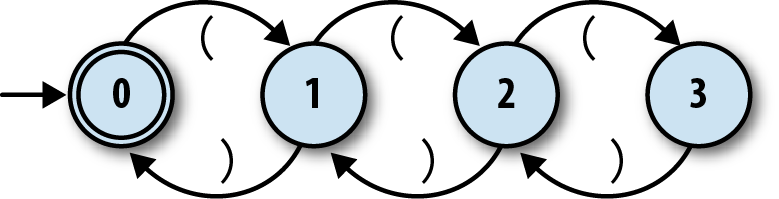
We can make a respectable start at designing an NFA for this job. Here’s one with four states:
Each state corresponds to a particular nesting level, and reading an opening or closing bracket moves the machine into a state for a higher or lower level respectively, with “no nesting” being the accept state. Since we’ve already implemented everything we need to simulate this NFA in Ruby, let’s fire it up:
>>rulebook=NFARulebook.new([FARule.new(0,'(',1),FARule.new(1,')',0),FARule.new(1,'(',2),FARule.new(2,')',1),FARule.new(2,'(',3),FARule.new(3,')',2)])=> #<struct NFARulebook rules=[…]>>>nfa_design=NFADesign.new(0,[0],rulebook)=> #<struct NFADesign start_state=0, accept_states=[0], rulebook=…>
Our NFA design works fine on certain inputs. It can tell that '(()' and '())' aren’t balanced and that
'(())' is, and it even has no problem spotting more
elaborate balanced strings like '(()(()()))':
>>nfa_design.accepts?('(()')=> false>>nfa_design.accepts?('())')=> false>>nfa_design.accepts?('(())')=> true>>nfa_design.accepts?('(()(()()))')=> true
But the design has a serious flaw: it’ll fail as soon as the brackets become nested more
than three levels deep. It doesn’t have enough states to keep track of the nesting in a string
like '(((())))', so it rejects that string even though the
brackets are clearly balanced:
>>nfa_design.accepts?('(((())))')=> false
We can fix this temporarily by adding more states. An NFA with five states can recognize
'(((())))' and any other balanced string with fewer than
five levels of nesting, and an NFA with ten, a hundred, or a thousand states can recognize any
balanced string whose nesting level stays within that machine’s hard limit. But how can we
design an NFA that can recognize any balanced string, to an arbitrary level
of nesting? It turns out that we can’t: a finite automaton must always have a finite number of
states, so for any given machine, there’s always a finite limit to how many levels of nesting it
can support, and we can always break it by asking about a string whose brackets nest one level
deeper than it can handle.
The underlying problem is that a finite automaton has only limited storage in the form of
its fixed collection of states, which means it has no way to keep track of an
arbitrary amount of information. In the case of the balanced brackets
problem, an NFA can easily count up to some maximum number baked into its design, but it can’t
keep counting indefinitely to accommodate inputs of any possible size.[30] This doesn’t matter for jobs that are inherently fixed in size, like matching the
literal string 'abc', or ones where there’s no need to keep
track of the amount of repetition, like matching the regular expression ab*c, but it does make finite automata unable to handle tasks where an
unpredictable amount of information needs to be stored up during the computation and reused
later.
It’s clear that there are limitations to these machines’ capabilities. If nondeterminism isn’t enough to make a finite automaton more capable, what else can we do to give it more power? The current problems stem from the machines’ limited storage, so let’s add some extra storage and see what happens.
Deterministic Pushdown Automata
We can solve the storage problem by extending a finite state machine with some dedicated scratch space where data can be kept during computation. This space gives the machine a sort of external memory in addition to the limited internal memory provided by its state—and as we’ll discover, having an external memory makes all the difference to a machine’s computational power.
Storage
A simple way to add storage to a finite automaton is to give it access to a stack, a last-in first-out data structure that characters can be pushed onto and then popped off again. A stack is a simple and restrictive data structure—only the top character is accessible at any one time, we have to discard the top character to find out what’s underneath it, and once we’ve pushed a sequence of characters onto the stack, we can only pop them off in reverse order—but it does neatly deal with the problem of limited storage. There’s no built-in limit to the size of a stack, so in principle, it can grow to hold as much data as necessary.[32]
A finite state machine with a built-in stack is called a pushdown automaton (PDA), and when that machine’s rules are deterministic, we call it a deterministic pushdown automaton (DPDA). Having access to a stack opens up new possibilities; for example, it’s easy to design a DPDA that recognizes balanced strings of brackets. Here’s how it works:
Give the machine two states, 1 and 2, with state 1 being the accept state.
Start the machine in state 1 with an empty stack.
When in state 1 and an opening bracket is read, push some character—let’s use
bfor “bracket”—onto the stack and move into state 2.When in state 2 and an opening bracket is read, push the character
bonto the stack.When in state 2 and a closing bracket is read, pop the character
boff the stack.When in state 2 and the stack is empty, move back into state 1.
This DPDA uses the size of the stack to count how many unclosed opening brackets it’s
seen so far. When the stack’s empty it means that every opening bracket has been closed, so
the string must be balanced. Watch how the stack grows and shrinks as the machine reads the
string '(()(()()))':
| State | Accepting? | Stack contents | Remaining input | Action |
| 1 | yes | | (()(()())) | read (, push b, go to state 2 |
| 2 | no | b | ()(()())) | read (, push b |
| 2 | no | bb | )(()())) | read ), pop b |
| 2 | no | b | (()())) | read (, push b |
| 2 | no | bb | ()())) | read (, push b |
| 2 | no | bbb | )())) | read ), pop b |
| 2 | no | bb | ())) | read (, push b |
| 2 | no | bbb | ))) | read ), pop b |
| 2 | no | bb | )) | read ), pop b |
| 2 | no | b | ) | read ), pop b |
| 2 | no | | | go to state 1 |
| 1 | yes | | | — |
Rules
The idea behind the balanced-brackets DPDA is straightforward, but there are some fiddly technical details to work out before we can actually build it. First of all, we have to decide exactly how pushdown automata rules should work. There are several design issues here:
Does every rule have to modify the stack, or read input, or change state, or all three?
Should there be two different kinds of rule for pushing and popping?
Do we need a special kind of rule for changing state when the stack is empty?
Is it okay to change state without reading from the input, like a free move in an NFA?
If a DPDA can change state spontaneously like that, what does “deterministic” mean?
We can answer all of these questions by choosing a single rule style that is flexible enough to support everything we need. We’ll break down a PDA rule into five parts:
The current state of the machine
The character that must be read from the input (optional)
The next state of the machine
The character that must be popped off the stack
The sequence of characters to push onto the stack after the top character has been popped off
The first three parts are familiar from DFA and NFA rules. If a rule doesn’t want the machine to change state, it can make the next state the same as the current one; if it doesn’t want to read any input (i.e., a free move), it can omit the input character, as long as that doesn’t make the machine nondeterministic (see Determinism).
The other two parts—a character to pop and a sequence of characters to push—are specific to PDAs. The assumption is that a PDA will always pop the top character off the stack, and then push some other characters onto the stack, every time it follows a rule. Each rule declares which character it wants to pop, and the rule will only apply when that character is on the top of the stack; if the rule wants that character to stay on the stack instead of getting popped, it can include it in the sequence of characters that get pushed back on afterward.
This five-part rule format doesn’t give us a way to write rules that apply when the
stack is empty, but we can work around that by choosing a special character to mark the
bottom of the stack—the dollar sign, $, is a popular
choice—and then checking for that character whenever we want to detect the empty stack. When
using this convention, it’s important that the stack never becomes truly empty, because no
rule can apply when there’s nothing on the top of the stack. The machine should start with
the special bottom symbol already on the stack, and any rule that pops that symbol must push
it back on again afterward.
It’s easy enough to rewrite the balanced-bracket DPDA’s rules in this format:
When in state 1 and an opening bracket is read, pop the character
$, push the charactersb$, and move into state 2.When in state 2 and an opening bracket is read, pop the character
b, push the charactersbb, and stay in state 2.When in state 2 and a closing bracket is read, pop the character
b, push no characters, and stay in state 2.When in state 2 (without reading any character), pop the character
$, push the character$, and move into state 1.
We can show these rules on a diagram of the machine. A DPDA
diagram looks a lot like an NFA diagram, except that each arrow needs to
be labelled with the characters that are popped and pushed by that rule
as well as the character that it reads from the input. If we use the
notation a;b/cd to label a rule that
reads a from the input, pops b from the stack, and then pushes cd onto the stack, the machine looks like
this:
Determinism
The next hurdle is to define exactly what it means for a PDA to be deterministic. For DFAs, we had
the “no contradictions” constraint: there should be no states where the machine’s next move
is ambiguous because of conflicting rules. The same idea applies to DPDAs, so for example,
we can only have one rule that applies when the machine’s in state 2, the next input
character is an opening bracket, and there’s a b on the
top of the stack. It’s even okay to write a free move rule that doesn’t read any input, as
long as there aren’t any other rules for the same state and top-of-stack character, because
that would create an ambiguity about whether or not a character should be read from the
input.
DFAs also have a “no omissions” constraint—there should be a rule for every possible
situation—but that idea becomes unwieldy for DPDAs because of the large number of possible
combinations of state, input character, and top-of-stack character. It’s conventional to
just ignore this constraint and allow DPDAs to specify only the interesting rules that they
need to get their job done, and assume that a DPDA will go into an implicit stuck
state if it gets into a situation where none of its rules apply. This is what
happens to our balanced-brackets DPDA when it reads a string like ')' or '())', because there’s no rule for
reading a closing bracket while in state 1.
Simulation
Now that we’ve dealt with the technical details, let’s build a Ruby simulation of a deterministic pushdown automaton so we can interact with it. We already did most of the hard work when we simulated DFAs and NFAs, so this’ll just take a bit of fine-tuning.
The most important thing we’re missing is a stack. Here’s one way
of implementing a Stack class:
classStack<Struct.new(:contents)defpush(character)Stack.new([character]+contents)enddefpopStack.new(contents.drop(1))enddeftopcontents.firstenddefinspect"#<Stack (#{top})#{contents.drop(1).join}>"endend
A Stack object stores its
contents in an underlying array and exposes simple #push and #pop operations to push characters onto the
stack and pop them off, plus a #top
operation to read the character at the top of the stack:
>>stack=Stack.new(['a','b','c','d','e'])=> #<Stack (a)bcde>>>stack.top=> "a">>stack.pop.pop.top=> "c">>stack.push('x').push('y').top=> "y">>stack.push('x').push('y').pop.top=> "x"
Note
This is a purely functional stack. The
#push and #pop methods are nondestructive: they each
return a new Stack instance rather
than modifying the existing one. Creating a new object every time
makes this implementation less efficient than a conventional stack
with destructive #push and #pop operations (and we could just use
Array directly if we wanted that)
but also makes it easier to work with, because we don’t need to worry
about the consequences of modifying a Stack that’s being used in more than one
place.
In Chapter 3, we saw that we can simulate a deterministic finite automaton by keeping track of just one piece of information—the DFA’s current state—and then using the rulebook to update that information each time a character is read from the input. But there are two important things to know about a pushdown automaton at each step of its computation: what its current state is, and what the current contents of its stack are. If we use the word configuration to refer to this combination of a state and a stack, we can talk about a pushdown automaton moving from one configuration to another as it reads input characters, which is easier than always having to refer to the state and stack separately. Viewed this way, a DPDA just has a current configuration, and the rulebook tells us how to turn the current configuration into the next configuration each time we read a character.
Here’s a PDAConfiguration class
to hold the configuration of a PDA—a state and a stack—and a PDARule class to represent one rule in a PDA’s
rulebook:[33]
classPDAConfiguration<Struct.new(:state,:stack)endclassPDARule<Struct.new(:state,:character,:next_state,:pop_character,:push_characters)defapplies_to?(configuration,character)self.state==configuration.state&&self.pop_character==configuration.stack.top&&self.character==characterendend
A rule only applies when the machine’s state, topmost stack character, and next input character all have the values it expects:
>>rule=PDARule.new(1,'(',2,'$',['b','$'])=> #<struct PDARulestate=1,character="(",next_state=2,pop_character="$",push_characters=["b", "$"]>>>configuration=PDAConfiguration.new(1,Stack.new(['$']))=> #<struct PDAConfiguration state=1, stack=#<Stack ($)>>>>rule.applies_to?(configuration,'(')=> true
For a finite automaton, following a rule just means changing from
one state to another, but a PDA rule updates the stack contents as well
as the state, so PDARule#follow needs
to take the machine’s current configuration as an argument and return
the next one:
classPDARuledeffollow(configuration)PDAConfiguration.new(next_state,next_stack(configuration))enddefnext_stack(configuration)popped_stack=configuration.stack.poppush_characters.reverse.inject(popped_stack){|stack,character|stack.push(character)}endend
Note
If we push several characters onto a stack and then pop them off, they come out in the opposite order:
>>stack=Stack.new(['$']).push('x').push('y').push('z')=> #<Stack (z)yx$>>>stack.top=> "z">>stack=stack.pop;stack.top=> "y">>stack=stack.pop;stack.top=> "x"
PDARule#next_stack
anticipates this by reversing the push_characters array before pushing its
characters onto the stack. For example, the last character in push_characters is the actually the
first one to be pushed onto the stack, so it’ll
be the last to be popped off again. This is just a convenience so that
we can read a rule’s push_characters as the sequence of
characters (in “popping order”) that will be on top of the stack after
the rule is applied, without having to worry about the mechanics of
how they get on there.
So, if we have a PDARule that
applies to a PDAConfiguration, we can
follow it to find out what the next state and stack will be:
>>rule.follow(configuration)=> #<struct PDAConfiguration state=2, stack=#<Stack (b)$>>
This gives us enough to implement a rulebook for DPDAs. The
implementation is very similar to the DFARulebook from Simulation:
classDPDARulebook<Struct.new(:rules)defnext_configuration(configuration,character)rule_for(configuration,character).follow(configuration)enddefrule_for(configuration,character)rules.detect{|rule|rule.applies_to?(configuration,character)}endend
Now we can assemble the rulebook for the balanced-brackets DPDA and try stepping through a few configurations and input characters by hand:
>>rulebook=DPDARulebook.new([PDARule.new(1,'(',2,'$',['b','$']),PDARule.new(2,'(',2,'b',['b','b']),PDARule.new(2,')',2,'b',[]),PDARule.new(2,nil,1,'$',['$'])])=> #<struct DPDARulebook rules=[…]>>>configuration=rulebook.next_configuration(configuration,'(')=> #<struct PDAConfiguration state=2, stack=#<Stack (b)$>>>>configuration=rulebook.next_configuration(configuration,'(')=> #<struct PDAConfiguration state=2, stack=#<Stack (b)b$>>>>configuration=rulebook.next_configuration(configuration,')')=> #<struct PDAConfiguration state=2, stack=#<Stack (b)$>>
Instead of doing this job manually, let’s use the rulebook to
build a DPDA object that can keep
track of the machine’s current configuration as it reads characters from
the input:
classDPDA<Struct.new(:current_configuration,:accept_states,:rulebook)defaccepting?accept_states.include?(current_configuration.state)enddefread_character(character)self.current_configuration=rulebook.next_configuration(current_configuration,character)enddefread_string(string)string.chars.eachdo|character|read_character(character)endendend
So we can create a DPDA, feed
it input, and see whether it’s accepted it:
>>dpda=DPDA.new(PDAConfiguration.new(1,Stack.new(['$'])),[1],rulebook)=> #<struct DPDA …>>>dpda.accepting?=> true>>dpda.read_string('(()');dpda.accepting?=> false>>dpda.current_configuration=> #<struct PDAConfiguration state=2, stack=#<Stack (b)$>>
Fine so far, but the rulebook we’re using contains a free move, so
the simulation needs to support free moves before it’ll work properly.
Let’s add a DPDARulebook helper
method for dealing with free moves, similar to the one in NFARulebook (see Free Moves):
classDPDARulebookdefapplies_to?(configuration,character)!rule_for(configuration,character).nil?enddeffollow_free_moves(configuration)ifapplies_to?(configuration,nil)follow_free_moves(next_configuration(configuration,nil))elseconfigurationendendend
DPDARulebook#follow_free_moves
will repeatedly follow any free moves that apply to the current
configuration, stopping when there are none:
>>configuration=PDAConfiguration.new(2,Stack.new(['$']))=> #<struct PDAConfiguration state=2, stack=#<Stack ($)>>>>rulebook.follow_free_moves(configuration)=> #<struct PDAConfiguration state=1, stack=#<Stack ($)>>
Warning
For the first time in our experiments with state machines, this introduces the possibility of an infinite loop in the simulation. A loop can happen whenever there’s a chain of free moves that begins and ends at the same state; the simplest example is when there’s one free move that doesn’t change the configuration at all:
>>DPDARulebook.new([PDARule.new(1,nil,1,'$',['$'])]).follow_free_moves(PDAConfiguration.new(1,Stack.new(['$'])))SystemStackError: stack level too deep
These infinite loops aren’t useful, so we’ll just take care to avoid them in any pushdown automata we design.
We also need to wrap the default implementation of DPDA#current_configuration to take advantage
of the rulebook’s free move support:
classDPDAdefcurrent_configurationrulebook.follow_free_moves(super)endend
Now we have a simulation of a DPDA that we can start up, feed characters to, and check for acceptance:
>>dpda=DPDA.new(PDAConfiguration.new(1,Stack.new(['$'])),[1],rulebook)=> #<struct DPDA …>>>dpda.read_string('(()(');dpda.accepting?=> false>>dpda.current_configuration=> #<struct PDAConfiguration state=2, stack=#<Stack (b)b$>>>>dpda.read_string('))()');dpda.accepting?=> true>>dpda.current_configuration=> #<struct PDAConfiguration state=1, stack=#<Stack ($)>>
If we wrap this simulation up in a DPDADesign as usual, we can easily check as
many strings as we like:
classDPDADesign<Struct.new(:start_state,:bottom_character,:accept_states,:rulebook)defaccepts?(string)to_dpda.tap{|dpda|dpda.read_string(string)}.accepting?enddefto_dpdastart_stack=Stack.new([bottom_character])start_configuration=PDAConfiguration.new(start_state,start_stack)DPDA.new(start_configuration,accept_states,rulebook)endend
As expected, our DPDA design can recognize complex strings of balanced brackets nested to arbitrary depth:
>>dpda_design=DPDADesign.new(1,'$',[1],rulebook)=> #<struct DPDADesign …>>>dpda_design.accepts?('(((((((((())))))))))')=> true>>dpda_design.accepts?('()(())((()))(()(()))')=> true>>dpda_design.accepts?('(()(()(()()(()()))()')=> false
There’s one final detail to take care of. Our simulation works perfectly on inputs that leave the DPDA in a valid state, but it blows up when the machine gets stuck:
>>dpda_design.accepts?('())')NoMethodError: undefined method `follow' for nil:NilClass
This happens because DPDARulebook#next_configuration assumes it
will be able to find an applicable rule, so we shouldn’t call it when
none of the rules apply. We’ll fix the problem by modifying DPDA#read_character to check for a usable rule
and, if there isn’t one, put the DPDA into a special stuck state that it
can never move out of:
classPDAConfigurationSTUCK_STATE=Object.newdefstuckPDAConfiguration.new(STUCK_STATE,stack)enddefstuck?state==STUCK_STATEendendclassDPDAdefnext_configuration(character)ifrulebook.applies_to?(current_configuration,character)rulebook.next_configuration(current_configuration,character)elsecurrent_configuration.stuckendenddefstuck?current_configuration.stuck?enddefread_character(character)self.current_configuration=next_configuration(character)enddefread_string(string)string.chars.eachdo|character|read_character(character)unlessstuck?endendend
Now the DPDA will gracefully become stuck instead of blowing up:
>>dpda=DPDA.new(PDAConfiguration.new(1,Stack.new(['$'])),[1],rulebook)=> #<struct DPDA …>>>dpda.read_string('())');dpda.current_configuration=> #<struct PDAConfiguration state=#<Object>, stack=#<Stack ($)>>>>dpda.accepting?=> false>>dpda.stuck?=> true>>dpda_design.accepts?('())')=> false
Nondeterministic Pushdown Automata
While the balanced-brackets machine does need the stack to do its job, it’s really only using the stack as a
counter, and its rules are only interested in the distinction between “the stack is empty” and
“the stack isn’t empty.” More sophisticated DPDAs will push more than one kind of symbol onto
the stack and make use of that information as they perform a computation. A simple example is
a machine for recognizing strings that contain equal numbers of two characters, say a and b:
Our simulation shows that it does the job:
>>rulebook=DPDARulebook.new([PDARule.new(1,'a',2,'$',['a','$']),PDARule.new(1,'b',2,'$',['b','$']),PDARule.new(2,'a',2,'a',['a','a']),PDARule.new(2,'b',2,'b',['b','b']),PDARule.new(2,'a',2,'b',[]),PDARule.new(2,'b',2,'a',[]),PDARule.new(2,nil,1,'$',['$'])])=> #<struct DPDARulebook rules=[…]>>>dpda_design=DPDADesign.new(1,'$',[1],rulebook)=> #<struct DPDADesign …>>>dpda_design.accepts?('ababab')=> true>>dpda_design.accepts?('bbbaaaab')=> true>>dpda_design.accepts?('baa')=> false
This is similar to the balanced-brackets machine, except its
behavior is controlled by which character is uppermost on the stack. An
a on the top of the stack means that
the machine’s seen a surplus of as, so
any extra as read from the input will
accumulate on the stack, and each b
read will pop an a off the stack to
cancel it out; conversely, when there’s a b on the stack, it’s the bs that accumulate and the as that cancel them out.
Even this DPDA isn’t taking full advantage of the stack, though. There’s never any
interesting history stored up beneath the top character, just a featureless pile of as or bs, so we can achieve the
same result by pushing only one kind of character onto the stack (i.e., treating it as a
simple counter again) and using two separate states to distinguish “counting surplus as” from “counting surplus bs”:
To really exploit the potential of the stack, we need a tougher problem that’ll force us
to store structured information. The classic example is recognizing palindromes: as we read the input string, character by character, we have to
remember what we see; once we pass the halfway point, we check our memory to decide whether
the characters we saw earlier are now appearing in reverse order. Here’s a DPDA that can
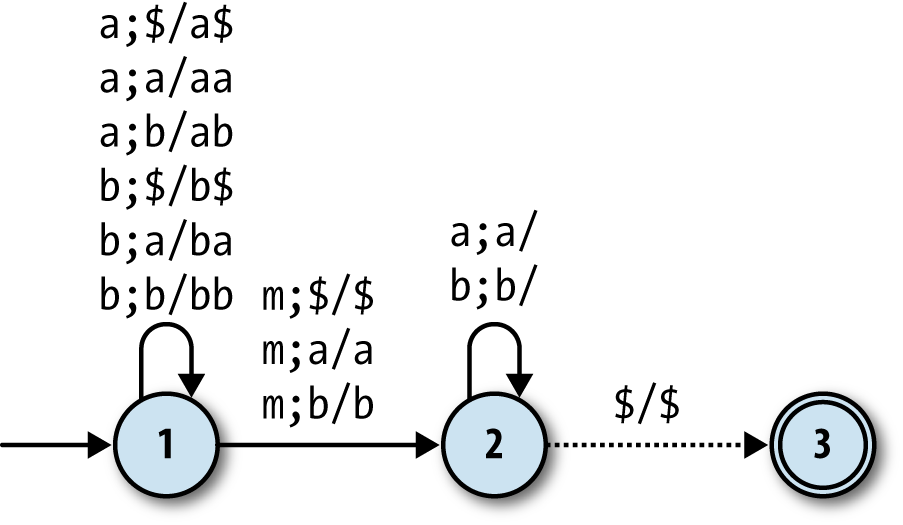
recognize palindromes made up of a and b characters, as long as they have an m character (for “middle”) at the halfway point of the string:
This machine starts in state 1, repeatedly reading as
and bs from the input and pushing them onto the stack. When
it reads an m, it moves into state 2, where it keeps
reading input characters while trying to pop each one off the stack. If
every character in the second half of the string matches the stack contents as they’re popped
off, the machine stays in state 2 and eventually hits the $
at the bottom of the stack, at which point it moves into state 3 and accepts the input string.
If any of the characters it reads while in state 2 don’t match what’s on the top of the stack,
there’s no rule for it to follow, so it’ll go into a stuck state and reject the string.
We can simulate this DPDA to check that it works:
>>rulebook=DPDARulebook.new([PDARule.new(1,'a',1,'$',['a','$']),PDARule.new(1,'a',1,'a',['a','a']),PDARule.new(1,'a',1,'b',['a','b']),PDARule.new(1,'b',1,'$',['b','$']),PDARule.new(1,'b',1,'a',['b','a']),PDARule.new(1,'b',1,'b',['b','b']),PDARule.new(1,'m',2,'$',['$']),PDARule.new(1,'m',2,'a',['a']),PDARule.new(1,'m',2,'b',['b']),PDARule.new(2,'a',2,'a',[]),PDARule.new(2,'b',2,'b',[]),PDARule.new(2,nil,3,'$',['$'])])=> #<struct DPDARulebook rules=[…]>>>dpda_design=DPDADesign.new(1,'$',[3],rulebook)=> #<struct DPDADesign …>>>dpda_design.accepts?('abmba')=> true>>dpda_design.accepts?('babbamabbab')=> true>>dpda_design.accepts?('abmb')=> false>>dpda_design.accepts?('baambaa')=> false
That’s great, but the m in the
middle of the input string is a cop-out. Why can’t we design a machine
that just recognizes palindromes—aa,
abba, babbaabbab, etc.—without having to put a marker
halfway through?
The machine has to change from state 1 to state 2 as soon as it reaches the halfway point of the string, and without a marker, it has no way of knowing when to do that. As we’ve seen before with NFAs, these “how do I know when to…?” problems can be solved by relaxing the determinism constraints and allowing the machine the freedom to make that vital state change at any point, so that it’s possible for it to accept a palindrome by following the right rule at the right time.
Unsurprisingly, a pushdown automaton without determinism constraints is called a nondeterministic pushdown automaton. Here’s one for recognizing palindromes with an even number of letters:[34]
This is identical to the DPDA version except for the rules that lead from state 1 to state
2: in the DPDA, they read an m from the input, but here
they’re free moves. This gives the NPDA the opportunity to change state anywhere during the
input string without needing a marker.
Simulation
A nondeterministic machine is more difficult to simulate than a deterministic
one, but we’ve already done the hard work for NFAs in Nondeterminism, and we can reuse the same ideas for NPDAs.
We need an NPDARulebook for holding a
nondeterministic collection of PDARules, and its implementation is almost
exactly the same as NFARulebook:
require'set'classNPDARulebook<Struct.new(:rules)defnext_configurations(configurations,character)configurations.flat_map{|config|follow_rules_for(config,character)}.to_setenddeffollow_rules_for(configuration,character)rules_for(configuration,character).map{|rule|rule.follow(configuration)}enddefrules_for(configuration,character)rules.select{|rule|rule.applies_to?(configuration,character)}endend
In Nondeterminism, we simulated an NFA by keeping track of a Set of possible states; here we’re simulating an NPDA with a
Set of possible
configurations.
Our rulebook needs the usual support for free moves, again
virtually identical to NFARulebook’s
implementation:
classNPDARulebookdeffollow_free_moves(configurations)more_configurations=next_configurations(configurations,nil)ifmore_configurations.subset?(configurations)configurationselsefollow_free_moves(configurations+more_configurations)endendend
And we need an NPDA class to
wrap up a rulebook alongside the Set
of current configurations:
classNPDA<Struct.new(:current_configurations,:accept_states,:rulebook)defaccepting?current_configurations.any?{|config|accept_states.include?(config.state)}enddefread_character(character)self.current_configurations=rulebook.next_configurations(current_configurations,character)enddefread_string(string)string.chars.eachdo|character|read_character(character)endenddefcurrent_configurationsrulebook.follow_free_moves(super)endend
This lets us step through a simulation of all possible configurations of an NPDA as each character is read:
>>rulebook=NPDARulebook.new([PDARule.new(1,'a',1,'$',['a','$']),PDARule.new(1,'a',1,'a',['a','a']),PDARule.new(1,'a',1,'b',['a','b']),PDARule.new(1,'b',1,'$',['b','$']),PDARule.new(1,'b',1,'a',['b','a']),PDARule.new(1,'b',1,'b',['b','b']),PDARule.new(1,nil,2,'$',['$']),PDARule.new(1,nil,2,'a',['a']),PDARule.new(1,nil,2,'b',['b']),PDARule.new(2,'a',2,'a',[]),PDARule.new(2,'b',2,'b',[]),PDARule.new(2,nil,3,'$',['$'])])=> #<struct NPDARulebook rules=[…]>>>configuration=PDAConfiguration.new(1,Stack.new(['$']))=> #<struct PDAConfiguration state=1, stack=#<Stack ($)>>>>npda=NPDA.new(Set[configuration],[3],rulebook)=> #<struct NPDA …>>>npda.accepting?=> true>>npda.current_configurations=> #<Set: {#<struct PDAConfiguration state=1, stack=#<Stack ($)>>,#<struct PDAConfiguration state=2, stack=#<Stack ($)>>,#<struct PDAConfiguration state=3, stack=#<Stack ($)>>}>>>npda.read_string('abb');npda.accepting?=> false>>npda.current_configurations=> #<Set: {#<struct PDAConfiguration state=1, stack=#<Stack (b)ba$>>,#<struct PDAConfiguration state=2, stack=#<Stack (a)$>>,#<struct PDAConfiguration state=2, stack=#<Stack (b)ba$>>}>>>npda.read_character('a');npda.accepting?=> true>>npda.current_configurations=> #<Set: {#<struct PDAConfiguration state=1, stack=#<Stack (a)bba$>>,#<struct PDAConfiguration state=2, stack=#<Stack ($)>>,#<struct PDAConfiguration state=2, stack=#<Stack (a)bba$>>,#<struct PDAConfiguration state=3, stack=#<Stack ($)>>}>
And finally an NPDADesign class
for testing strings directly:
classNPDADesign<Struct.new(:start_state,:bottom_character,:accept_states,:rulebook)defaccepts?(string)to_npda.tap{|npda|npda.read_string(string)}.accepting?enddefto_npdastart_stack=Stack.new([bottom_character])start_configuration=PDAConfiguration.new(start_state,start_stack)NPDA.new(Set[start_configuration],accept_states,rulebook)endend
Now we can check that our NPDA actually does recognize palindromes:
>>npda_design=NPDADesign.new(1,'$',[3],rulebook)=> #<struct NPDADesign …>>>npda_design.accepts?('abba')=> true>>npda_design.accepts?('babbaabbab')=> true>>npda_design.accepts?('abb')=> false>>npda_design.accepts?('baabaa')=> false
Looks good! Nondeterminism has apparently given us the power to recognize languages that deterministic machines can’t handle.
Nonequivalence
But wait: we saw in Equivalence that nondeterministic machines without a stack are exactly equivalent in power to deterministic ones. Our Ruby NFA simulation behaved like a DFA—moving between a finite number of “simulation states” as it read each character of the input string—which gave us a way to turn any NFA into a DFA that accepts the same strings. So has nondeterminism really given us any extra power, or does our Ruby NPDA simulation just behave like a DPDA? Is there an algorithm for converting any nondeterministic pushdown automaton into a deterministic one?
Well, no, it turns out that there isn’t. The NFA-to-DFA trick only works because we can use a single DFA state to represent many possible NFA states. To simulate an NFA, we only need to keep track of what states it could currently be in, then pick a different set of possible states each time we read an input character, and a DFA can easily do that job if we give it the right rules.
But that trick doesn’t work for PDAs: we can’t usefully represent multiple NPDA configurations as a single DPDA configuration. The problem, unsurprisingly, is the stack. An NPDA simulation needs to know all the characters that could currently be on top of the stack, and it must be able to pop and push several of the simulated stacks simultaneously. There’s no way to combine all the possible stacks into a single stack so that a DPDA can still see all the topmost characters and access every possible stack individually. We didn’t have any difficulty writing a Ruby program to do all this, but a DPDA just isn’t powerful enough to handle it.
So unfortunately, our NPDA simulation does not behave like a DPDA, and there isn’t an NPDA-to-DPDA algorithm. The unmarked palindrome problem is an example of a job where an NPDA can do something that a DPDA can’t, so nondeterministic pushdown automata really do have more power than deterministic ones.
Parsing with Pushdown Automata
Regular Expressions showed how nondeterministic finite automata can be used to implement regular expression matching. Pushdown automata have an important practical application too: they can be used to parse programming languages.
We already saw in Implementing Parsers how to use Treetop to build a parser for part of the Simple language. Treetop parsers use a single parsing expression grammar to describe the complete syntax of the language being parsed, but that’s a relatively modern idea. A more traditional approach is to break the parsing process apart into two separate stages:
- Lexical analysis
Read a raw string of characters and turn it into a sequence of tokens. Each token represents an individual building block of program syntax, like “variable name,” “opening bracket,” or “
whilekeyword.” A lexical analyzer uses a language-specific set of rules called a lexical grammar to decide which sequences of characters should produce which tokens. This stage deals with messy character-level details like variable-naming rules, comments, and whitespace, leaving a clean sequence of tokens for the next stage to consume.- Syntactic analysis
Read a sequence of tokens and decide whether they represent a valid program according to the syntactic grammar of the language being parsed. If the program is valid, the syntactic analyzer may produce additional information about its structure (e.g., a parse tree).
Lexical Analysis
The lexical analysis stage is usually pretty straightforward. It can be done with regular expressions (and therefore by an NFA), because it involves simply matching a flat sequence of characters against some rules and deciding whether those characters look like a keyword, a variable name, an operator, or whatever else. Here’s some quick-and-dirty Ruby code to chop up a Simple program into tokens:
classLexicalAnalyzer<Struct.new(:string)GRAMMAR=[{token:'i',pattern:/if/},# if keyword{token:'e',pattern:/else/},# else keyword{token:'w',pattern:/while/},# while keyword{token:'d',pattern:/do-nothing/},# do-nothing keyword{token:'(',pattern:/\(/},# opening bracket{token:')',pattern:/\)/},# closing bracket{token:'{',pattern:/\{/},# opening curly bracket{token:'}',pattern:/\}/},# closing curly bracket{token:';',pattern:/;/},# semicolon{token:'=',pattern:/=/},# equals sign{token:'+',pattern:/\+/},# addition sign{token:'*',pattern:/\*/},# multiplication sign{token:'<',pattern:/</},# less-than sign{token:'n',pattern:/[0-9]+/},# number{token:'b',pattern:/true|false/},# boolean{token:'v',pattern:/[a-z]+/}# variable name]defanalyze[].tapdo|tokens|whilemore_tokens?tokens.push(next_token)endendenddefmore_tokens?!string.empty?enddefnext_tokenrule,match=rule_matching(string)self.string=string_after(match)rule[:token]enddefrule_matching(string)matches=GRAMMAR.map{|rule|match_at_beginning(rule[:pattern],string)}rules_with_matches=GRAMMAR.zip(matches).reject{|rule,match|match.nil?}rule_with_longest_match(rules_with_matches)enddefmatch_at_beginning(pattern,string)/\A#{pattern}/.match(string)enddefrule_with_longest_match(rules_with_matches)rules_with_matches.max_by{|rule,match|match.to_s.length}enddefstring_after(match)match.post_match.lstripendend
Note
This implementation uses single characters as tokens—w means “the while keyword,” + means “the addition sign,” and so
on—because soon we’re going to be feeding those tokens to a PDA, and
our Ruby PDA simulations expect to read characters as input.
Single-character tokens are good enough for a basic demonstration where we don’t need to retain the names of variables or the values of literals. In a real parser, however, we’d want to use a proper data structure to represent tokens so they could communicate more information than just “some unknown variable name” or “some unknown Boolean.”
By creating a LexicalAnalyzer
instance with a string of Simple code
and calling its #analyze method, we
can get back an array of tokens showing how the code breaks down into
keywords, operators, punctuation, and other pieces of syntax:
>>LexicalAnalyzer.new('y = x * 7').analyze=> ["v", "=", "v", "*", "n"]>>LexicalAnalyzer.new('while (x < 5) { x = x * 3 }').analyze=> ["w", "(", "v", "<", "n", ")", "{", "v", "=", "v", "*", "n", "}"]>>LexicalAnalyzer.new('if (x < 10) { y = true; x = 0 } else { do-nothing }').analyze=> ["i", "(", "v", "<", "n", ")", "{", "v", "=", "b", ";", "v", "=", "n", "}", "e","{", "d", "}"]
Note
Choosing the rule with the longest match allows the lexical analyzer to handle variables whose names would otherwise cause them to be wrongly identified as keywords:
>>LexicalAnalyzer.new('x = false').analyze=> ["v", "=", "b"]>>LexicalAnalyzer.new('x = falsehood').analyze=> ["v", "=", "v"]
There are other ways of dealing with this problem. One alternative would be to write
more restrictive regular expressions in the rules: if the Boolean rule used the pattern
/(true|false)(?![a-z])/, then it wouldn’t match the
string 'falsehood' in the first place.
Syntactic Analysis
Once we’ve done the easy work of turning a string into tokens, the harder problem is to decide whether those tokens represent a syntactically valid Simple program. We can’t use regular expressions or NFAs to do it—Simple’s syntax allows arbitrary nesting of brackets, and we already know that finite automata aren’t powerful enough to recognize languages like that. It is possible to use a pushdown automaton to recognize valid sequences of tokens, though, so let’s see how to construct one.
First we need a syntactic grammar that describes how tokens may be combined to form programs. Here’s part of a grammar for Simple, based on the structure of the Treetop grammar in Implementing Parsers:
<statement> ::= <while> | <assign>
<while> ::= 'w' '(' <expression> ')' '{' <statement> '}'
<assign> ::= 'v' '=' <expression>
<expression> ::= <less-than>
<less-than> ::= <multiply> '<' <less-than> | <multiply>
<multiply> ::= <term> '*' <multiply> | <term>
<term> ::= 'n' | 'v'This is called a context-free grammar (CFG).[35] Each rule has a symbol on the lefthand side and one or
more sequences of symbols and tokens on the right. For example, the rule <statement> ::= <while> | <assign> means that
a Simple statement is either a while loop or an assignment, and <assign> ::=
'v' '=' <expression> means that an assignment statement consists of a
variable name followed by an equals sign and an expression.
The CFG is a static description of Simple’s structure, but we can also think of
it as a set of rules for generating Simple programs. Starting from the <statement> symbol, we can apply the
grammar rules to recursively expand symbols until only tokens remain.
Here’s one of many ways to fully expand <statement> according to the
rules:
<statement> → <assign>
→ 'v' '=' <expression>
→ 'v' '=' <less-than>
→ 'v' '=' <multiply>
→ 'v' '=' <term> '*' <multiply>
→ 'v' '=' 'v' '*' <multiply>
→ 'v' '=' 'v' '*' <term>
→ 'v' '=' 'v' '*' 'n'This tells us that 'v' '=' 'v' '*'
'n' represents a syntactically valid program, but we want the
ability to go in the opposite direction: to
recognize valid programs, not generate them. When
we get a sequence of tokens out of the lexical analyzer, we’d like to
know whether it’s possible to expand the <statement> symbol into those tokens by
applying the grammar rules in some order. Fortunately, there’s a way to
turn a context-free grammar into a nondeterministic pushdown automaton
that can make exactly this decision.
The technique for converting a CFG into a PDA works like this:
Pick a character to represent each symbol from the grammar. In this case, we’ll use the uppercase initial of each symbol—
Sfor<statement>,Wfor<while>, and so on—to distinguish them from the lowercase characters we’re using as tokens.Use the PDA’s stack to store characters that represent grammar symbols (
S,W,A,E, …) and tokens (w,v,=,*, …). When the PDA starts, have it immediately push a symbol onto the stack to represent the structure it’s trying to recognize. We want to recognize Simple statements, so our PDA will begin by pushingSonto the stack:>>start_rule=PDARule.new(1,nil,2,'$',['S','$'])=> #<struct PDARule …>Translate the grammar rules into PDA rules that expand symbols on the top of the stack without reading any input. Each grammar rule describes how to expand a single symbol into a sequence of other symbols and tokens, and we can turn that description into a PDA rule that pops a particular symbol’s character off the stack and pushes other characters on:
>>symbol_rules=[# <statement> ::= <while> | <assign>PDARule.new(2,nil,2,'S',['W']),PDARule.new(2,nil,2,'S',['A']),# <while> ::= 'w' '(' <expression> ')' '{' <statement> '}'PDARule.new(2,nil,2,'W',['w','(','E',')','{','S','}']),# <assign> ::= 'v' '=' <expression>PDARule.new(2,nil,2,'A',['v','=','E']),# <expression> ::= <less-than>PDARule.new(2,nil,2,'E',['L']),# <less-than> ::= <multiply> '<' <less-than> | <multiply>PDARule.new(2,nil,2,'L',['M','<','L']),PDARule.new(2,nil,2,'L',['M']),# <multiply> ::= <term> '*' <multiply> | <term>PDARule.new(2,nil,2,'M',['T','*','M']),PDARule.new(2,nil,2,'M',['T']),# <term> ::= 'n' | 'v'PDARule.new(2,nil,2,'T',['n']),PDARule.new(2,nil,2,'T',['v'])]=> [#<struct PDARule …>, #<struct PDARule …>, …]For example, the rule for assignment statements says that the
<assign>symbol can be expanded to the tokensvand=followed by the<expression>symbol, so we have a corresponding PDA rule that spontaneously pops anAoff the stack and pushes the charactersv=Eback on. The<statement>rule says that we can replace the<statement>symbol with a<while>or<assign>symbol; we’ve turned that into one PDA rule that pops anSfrom the stack and replaces it with aW, and another rule that pops anSand pushes anA.Give every token character a PDA rule that reads that character from the input and pops it off the stack:
>>token_rules=LexicalAnalyzer::GRAMMAR.mapdo|rule|PDARule.new(2,rule[:token],2,rule[:token],[])end=> [#<struct PDARule …>, #<struct PDARule …>, …]These token rules work in opposition to the symbol rules. The symbol rules tend to make the stack larger, sometimes pushing several characters to replace the one that’s been popped; the token rules always make the stack smaller, consuming input as they go.
Finally, make a PDA rule that will allow the machine to enter an accept state if the stack becomes empty:
>>stop_rule=PDARule.new(2,nil,3,'$',['$'])=> #<struct PDARule …>
Now we can build a PDA with these rules and feed it a string of
tokens to see whether it recognizes them. The rules generated by the
Simple grammar are
nondeterministic—there’s more than one applicable rule whenever the
character S, L, M, or
T is topmost on the stack—so it’ll
have to be an NPDA:
>>rulebook=NPDARulebook.new([start_rule,stop_rule]+symbol_rules+token_rules)=> #<struct NPDARulebook rules=[…]>>>npda_design=NPDADesign.new(1,'$',[3],rulebook)=> #<struct NPDADesign …>>>token_string=LexicalAnalyzer.new('while (x < 5) { x = x * 3 }').analyze.join=> "w(v<n){v=v*n}">>npda_design.accepts?(token_string)=> true>>npda_design.accepts?(LexicalAnalyzer.new('while (x < 5 x = x * }').analyze.join)=> false
To show exactly what’s going on, here’s one possible execution of the NPDA when it’s fed
the string 'w(v<n){v=v*n}':
| State | Accepting? | Stack contents | Remaining input | Action |
| 1 | no | $ | w(v<n){v=v*n} | push S, go to state
2 |
| 2 | no | S$ | w(v<n){v=v*n} | pop S, push W |
| 2 | no | W$ | w(v<n){v=v*n} | pop W, push w(E){S} |
| 2 | no | w(E){S}$ | w(v<n){v=v*n} | read w, pop w |
| 2 | no | (E){S}$ | (v<n){v=v*n} | read (, pop ( |
| 2 | no | E){S}$ | v<n){v=v*n} | pop E, push L |
| 2 | no | L){S}$ | v<n){v=v*n} | pop L, push M<L |
| 2 | no | M<L){S}$ | v<n){v=v*n} | pop M, push T |
| 2 | no | T<L){S}$ | v<n){v=v*n} | pop T, push v |
| 2 | no | v<L){S}$ | v<n){v=v*n} | read v, pop v |
| 2 | no | <L){S}$ | <n){v=v*n} | read <, pop
< |
| 2 | no | L){S}$ | n){v=v*n} | pop L, push M |
| 2 | no | M){S}$ | n){v=v*n} | pop M, push T |
| 2 | no | T){S}$ | n){v=v*n} | pop T, push n |
| 2 | no | n){S}$ | n){v=v*n} | read n, pop n |
| 2 | no | ){S}$ | ){v=v*n} | read ), pop ) |
| 2 | no | {S}$ | {v=v*n} | read {, pop { |
| 2 | no | S}$ | v=v*n} | pop S, push A |
| 2 | no | A}$ | v=v*n} | pop A, push v=E |
| 2 | no | v=E}$ | v=v*n} | read v, pop v |
| 2 | no | =E}$ | =v*n} | read =, pop = |
| 2 | no | E}$ | v*n} | pop E, push L |
| 2 | no | L}$ | v*n} | pop L, push M |
| 2 | no | M}$ | v*n} | pop M, push T*M |
| 2 | no | T*M}$ | v*n} | pop T, push v |
| 2 | no | v*M}$ | v*n} | read v, pop v |
| 2 | no | *M}$ | *n} | read *, pop * |
| 2 | no | M}$ | n} | pop M, push T |
| 2 | no | T}$ | n} | pop T, push n |
| 2 | no | n}$ | n} | read n, pop n |
| 2 | no | }$ | } | read }, pop } |
| 2 | no | $ | | go to state 3 |
| 3 | yes | $ | | — |
This execution trace shows us how the machine ping-pongs between symbol and token rules: the symbol rules repeatedly expand the symbol on the top of the stack until it gets replaced by a token, then the token rules consume the stack (and the input) until they hit a symbol. This back and forth eventually results in an empty stack as long as the input string can be generated by the grammar rules.[36]
How does the PDA know which rule to choose at each step of execution? Well, that’s the power of nondeterminism: our NPDA simulation tries all possible rules, so as long as there’s some way of getting to an empty stack, we’ll find it.
Practicalities
This parsing procedure relies on nondeterminism, but in real applications, it’s best to avoid nondeterminism, because a deterministic PDA is much faster and easier to simulate than a nondeterministic one. Fortunately, it’s almost always possible to eliminate nondeterminism by using the input tokens themselves to make decisions about which symbol rule to apply at each stage—a technique called lookahead—but that makes the translation from CFG to PDA more complicated.
It’s also not really good enough to only be able to recognize valid
programs. As we saw in Implementing Parsers, the whole point of parsing a
program is to turn it into a structured representation that we can then do something useful
with. In practice, we can create this representation by instrumenting our PDA simulation to
record the sequence of rules it follows to reach an accept state, which provides enough
information to construct a parse tree. For example, the above execution trace shows us how
the symbols on the stack get expanded to form the desired sequence of tokens, and that tells
us the shape of the parse tree for the string 'w(v<n){v=v*n}':
How Much Power?
In this chapter, we’ve encountered two new levels of computing power: DPDAs are more powerful than DFAs and NFAs, and NPDAs are more powerful again. Having access to a stack, it seems, gives pushdown automata a bit more power and sophistication than finite automata.
The main consequence of having a stack is the ability to recognize certain languages that finite automata aren’t capable of recognizing, like palindromes and strings of balanced brackets. The unlimited storage provided by a stack lets a PDA remember arbitrary amounts of information during a computation and refer back to it later.
Unlike finite automata, a PDA can loop indefinitely without reading any input, which is curious even if it’s not particularly useful. A DFA can only ever change state by consuming a character of input, and although an NFA can change state spontaneously by following a free move, it can only do that a finite number of times before it ends up back where it started. A PDA, on the other hand, can sit in a single state and keep pushing characters onto its stack forever, never once repeating the same configuration.
Pushdown automata can also control themselves to a limited extent. There’s a feedback loop between the rules and the stack—the contents of the stack affect which rules the machine can follow, and following a rule will affect the stack contents—which allows a PDA to store away information on the stack that will influence its future execution. Finite automata rely upon a similar feedback loop between their rules and current state, but the feedback is less powerful because the current state is completely forgotten when it changes, whereas pushing characters onto a stack preserves the old contents for later use.
Okay, so PDAs are a bit more powerful, but what are their limitations? Even if we’re only
interested in the kinds of pattern-matching applications we’ve already seen, pushdown automata
are still seriously limited by the way a stack works. There’s no random access to stack
contents below the topmost character, so if a machine wants to read a character that’s buried
halfway down the stack, it has to pop everything above it. Once characters have been popped,
they’re gone forever; we designed a PDA to recognize strings with equal numbers of as and bs, but we can’t adapt
it to recognize strings with equal numbers of three different types of
character ('abc', 'aabbcc', 'aaabbbccc', …) because the
information about the number of as gets destroyed by the
process of counting the bs.
Aside from the number of times that pushed characters can be used,
the last-in-first-out nature of a stack causes a problem with the order
in which information is stored and retrieved. PDAs can recognize palindromes, but they can’t
recognize doubled-up strings like 'abab' and 'baaabaaa', because once information has been pushed onto a stack,
it can only be consumed in reverse order.
If we move away from the specific problem of recognizing strings and try to treat these machines as a model of general-purpose computers, we can see that DFAs, NFAs, and PDAs are still a long way from being properly useful. For starters, none of them has a decent output mechanism: they can communicate success by going into an accept state, but can’t output even a single character (much less a whole string of characters) to indicate a more detailed result. This inability to send information back out into the world means that they can’t implement even a simple algorithm like adding two numbers together. And like finite automata, an individual PDA has a fixed program; there isn’t an obvious way to build a PDA that can somehow read a program from its input and run it.
All of these weaknesses mean that we need a better model of computation to really investigate what computers are capable of, and that’s exactly what the next chapter is about.
[29] This isn’t quite the same as accepting strings that merely contain equal numbers of
opening and closing brackets. The strings '()' and
')(' each contain a single opening and closing bracket,
but only '()' is balanced.
[30] This doesn’t mean that an input string can ever actually be infinite, just that we can make it as finitely large as we like.
[31] Briefly, this algorithm works by converting an NFA into a generalized nondeterministic finite automaton (GNFA), a finite state machine where each rule is labeled with a regular expression instead of a single character, and then repeatedly merging the states and rules of the GNFA until there are only two states and one rule left. The regular expression that labels that final rule always matches the same strings as the original NFA.
[32] Of course, any real-world implementation of a stack is always going to be limited by the size of a computer’s RAM, or the free space on its hard drive, or the number of atoms in the universe, but for the purposes of our thought experiment, we’ll assume that none of those constraints exist.
[33] These class names begin with PDA, rather than DPDA, because their implementations don’t
make any assumptions about determinism, so they’d work just as well
for simulating a nondeterministic PDA.
[34] The “even number of letters” restriction keeps the machine
simple: a palindrome of length 2n can be accepted
by pushing n characters onto the stack and then
popping n characters off. To recognize
any palindrome requires a few more rules going
from state 1 to state 2.
[35] The grammar is “context free” in the sense that its rules don’t say anything about the context in which each piece of syntax may appear; an assignment statement always consists of a variable name, equals sign, and expression, regardless of what other tokens surround it. Not all imaginable languages can be described by this kind of grammar, but almost all programming languages can.
[36] This algorithm is called LL parsing. The first L stands for “left-to-right,” because the input string is read in that direction, and the second L stands for “left derivation,” because it’s always the leftmost (i.e., uppermost) symbol on the stack that gets expanded.
Get Understanding Computation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.