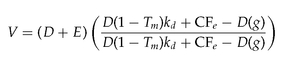Valuation: Measuring and Managing the Value of Companies, Fifth Edition

APPENDIX C

Derivation of Free Cash Flow, Weighted Average Cost of Capital, and Adjusted Present Value

In Chapter 6, we numerically demonstrate the equivalence of enterprise discounted cash flow (DCF), adjusted present value (APV), and the cash-flow-to-equity valuation when leverage (as measured by the market-based debt-to-equity ratio) is constant. In this appendix, we derive the key terms in each model—namely, free cash flow (FCF) and the weighted average cost of capital (WACC)—and demonstrate their equivalence algebraically.

To simplify the analysis, we assume cash flows to equity are growing at a constant rate, g. This way we can use growth perpetuities to analyze the relationship between methods.⁵⁰⁹

ENTERPRISE DISCOUNTED CASH FLOW

By definition, enterprise value equals the market value of debt plus the market value of equity:

V = D + E

To examine the components of enterprise value, multiply the right side of the equation by a complex fraction equivalent to 1 (the numerator equals the denominator, an algebraic trick we will use many times):

(C.1)

where

T_m = marginal tax rate k_d = cost of debt CF_e = cash flow to equity holders g = growth in cash flow to equity holders

Over the next few steps, the fraction’s numerator will be converted to free cash flow (FCF). We will show later that the denominator equals the weighted average cost of capital. Start by defining FCF: