VLSI Digital Signal Processing Systems: Design and Implementation

15.3    MULTIPLE CONSTANT MULTIPLICATION

Subexpression elimination can be applied to a set of constant multipliers that multiply a common variable. The multiple constant multiplication (MCM) problem [1] determines how subexpression elimination can be applied to the set of constant multipliers so that the number of shifts and additions required for implementation is minimized. A general framework and algorithm for solving this problem has been presented in [1], One of the attractive features of this algorithm is its versatility and adaptability to various forms of the MCM problem. The algorithm uses an iterative matching process that consists of 5 basic steps.

Table 15.1    Binary Representation of Constants from Example 15.3.1

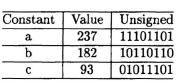
Step 1:    Express each constant in the set using a binary format (such as signed, unsigned, two’s complement representation).

Step 2:    Determine the number of bit-wise matches (nonzero bits) between all of the constants in the set.

Step 3:    Choose the best match.

Step 4:    Eliminate the redundancy from the best match. Return the remainders and the redundancy to the set of coefficients.

Step 5:    Repeat Steps 2–4 until no improvement is achieved.

Although a few additional preprocessing steps can reduce the CPU run-time of the algorithm, these 5 steps represent the primary processing steps required to solve the MCM problem. Several applications of the ...