VLSI Digital Signal Processing Systems: Design and Implementation

7.5    MATRIX-MATRIX MULTIPLICATION AND 2D SYSTOLIC ARRAY DESIGN

In this section, systolic arrays are designed for matrix-matrix multiplication [4]. The DG for this problem corresponds to a three-dimensional (3D) space representation. Linear projection is used to design 2D systolic arrays for matrix-matrix multiplication.

Given 2 matrices A and B, we can denote their product as C = AB, where A, B, and C are n × n matrices. For n = 2, we have

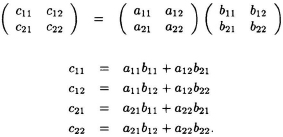
These equations can be represented in a space representation as shown in Fig. 7.17.

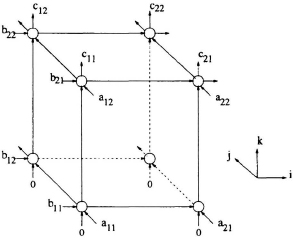
Fig. 7.17    Systolic array architecture of the matrix product computation.

From the space diagram, we can write the iteration in standard output RIA form as follows:

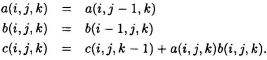
The corresponding RDG is shown in Fig. 7.18. Now, applying the scheduling inequality for each edge in the RDG s^Te + γ_y − γ_x ≥ T_x and assuming

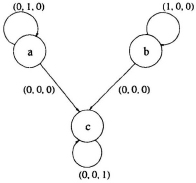
Fig. 7.18    Reduce dependence graph of the matrix product computation.

T_mult−add = 1 and T_com = 0, we have,

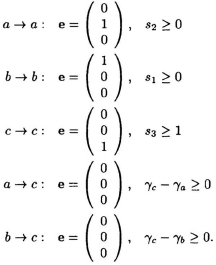
For linear scheduling, γ_a = γ_b = γ_c = 0. Consider ...