VLSI Digital Signal Processing Systems: Design and Implementation

7.8    PROBLEMS

1. For the DG shown in Fig. 7.24,

   (a)  Which of the following sets of scheduling and projection are permissible?

     i.  s = [1 0]^T, d = [1 0]^T

    ii.  s = [1 2]^T, d = [2 − 1]^T

   iii.  s = [1 1]^T, d = [1 0]^T

   iv.  s = [1 − 2]^T, d = [1 0]^T

   (b)  Derive the projected systolic array for each permissible set.

2. Draw the space-time mapping of design R₁.
3. Using one or more transformations such as edge reversal, associativity, slow-down, retiming, and pipelining, derive design R₁ from B₂.
4. For the two designs R₂ and dual R₂, draw the architecture block diagrams and their space-time mappings.
5. Using one or more transformations such as edge reversal, associativity, slow-down, retiming, and pipelining, show all steps needed to obtain dual R₂ from R₂.
6. Draw the space-time representation and the systolic architecture of the design W1 with 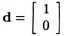, p^T = [ 0 1 ], and s^T = [ 2 1 ].
7. Derive design W₁ from design F using transformations such as edge reversal, associativity, slow-down, retiming, and pipelining.
8. For the two designs W₂ and dual W₂, draw the architecture block diagrams and their space-time mappings. Why are these two architectures dual of each other?
9. Consider the DG of a 5-tap convolution filter shown in Fig. 7.25. Assume that the inputs and the coefficients can be broadcast (with no time delay) to all processors simultaneously or can be delayed for fully systolic design. Further assume that ...