7.3 THE MINIMUM SPANNING TREE
MSTs are emblematic example of topological structures commonly used in communication networks. In a graph G = (V, E), an MST is a connected subset of the graph that contains all the vertices and minimizes the overall sum of its edge lengths (or more generally their weight). A well-known centralized algorithm to build such a structure is the Kruskal's algorithm, which mainly works as follows. All edges of E are sorted in the increasing weight order, and a new empty set E′ is created. For each edge e in the ordered set E, e is added to E′ if it does not create a loop in G′ = (V, E′). The resulting graph G′ is an MST of G.
The Figure 7.1 gives an example of MST that has been built over a random UDG. As usual, in wireless networks, the length of the edges was used as their weight. Note that if several edges have the same length, then several equivalent MSTs may exist, but this nondeterminism can be easily broken based on additional parameters (such as a comparison between nodes IDs).
An interesting fact about the MST is that its longest edge also corresponds to the optimal common transmission radius (i.e., the minimal radius such that network connectivity is preserved). This follows directly from Kruskal's algorithm, this edge being the last added edge in E′.
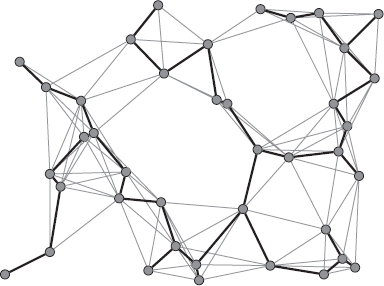
Figure 7.1 A minimum spanning tree on top of a random unit graph.
Considering a few related results, ...
Get Wireless Sensor and Actuator Networks: Algorithms and Protocols for Scalable Coordination and Data Communication now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

