Feedback Control for Computer Systems

Chapter 24. Root Locus Techniques

As we saw in Chapter 23, the location of the poles and zeros of the transfer function determines the system’s dynamic behavior. We can therefore change the dynamics of the system by moving the poles and zeros to more desirable positions, a method known as “pole placement.” The easiest way to do this is by adjusting the controller gains—that is by “tuning” the controller. (See Chapter 9 for more hands-on techniques of controller tuning.)

As the controller gains are varied, the poles and zeros of the closed-loop transfer function trace out curves in the complex plane that are called root locus curves. A root locus diagram is a plot of the complex plane showing the root locus curves^[25] as the gain is increased from zero toward infinity. Given such a diagram, we can choose the gain value that moves the dominant poles closest to their desired locations.

Because the structure of transfer functions is not arbitrary (they tend to be rational polynomials), we can make some general statements about global features of the corresponding root locus diagrams. These rules are discussed next.

Construction of Root Locus Diagrams

Root locus diagrams are usually drawn for closed-loop systems, such as the one depicted in Figure 24-1. This system has the closed-loop transfer function

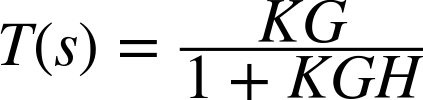
This function has a pole when the denominator becomes zero, so the condition for a pole is ...