Chapter 11Applications of Slicing to Combinatorics
11.1 Introduction
A combinatorial problem usually requires enumerating, counting, or ascertaining existence of structures that satisfy a given property 
in a set of structures 
. We now show that slicing can be used for solving such problems mechanically and efficiently. Specifically, we give an efficient (polynomial time) algorithm to enumerate, count, or detect structures that satisfy 
when the total set of structures is large but the set of structures satisfying 
is small. We illustrate the slicing method by analyzing problems in integer partitions, set families, and the set of permutations.
Consider the following combinatorial problems:
- (Q1) Count the number of subsets of the set
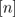(the set {
}), which have size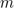 
and do not contain any ...
Get Introduction to Lattice Theory with Computer Science Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
