Chapter 4. Convolutional Neural Networks
In this chapter we introduce convolutional neural networks (CNNs) and the building blocks and methods associated with them. We start with a simple model for classification of the MNIST dataset, then we introduce the CIFAR10 object-recognition dataset and apply several CNN models to it. While small and fast, the CNNs presented in this chapter are highly representative of the type of models used in practice to obtain state-of-the-art results in object-recognition tasks.
Introduction to CNNs
Convolutional neural networks have gained a special status over the last few years as an especially promising form of deep learning. Rooted in image processing, convolutional layers have found their way into virtually all subfields of deep learning, and are very successful for the most part.
The fundamental difference between fully connected and convolutional neural networks is the pattern of connections between consecutive layers. In the fully connected case, as the name might suggest, each unit is connected to all of the units in the previous layer. We saw an example of this in Chapter 2, where the 10 output units were connected to all of the input image pixels.
In a convolutional layer of a neural network, on the other hand, each unit is connected to a (typically small) number of nearby units in the previous layer. Furthermore, all units are connected to the previous layer in the same way, with the exact same weights and structure. This leads to an operation known as convolution, giving the architecture its name (see Figure 4-1 for an illustration of this idea). In the next section, we go into the convolution operation in some more detail, but in a nutshell all it means for us is applying a small “window” of weights (also known as filters) across an image, as illustrated in Figure 4-2 later.
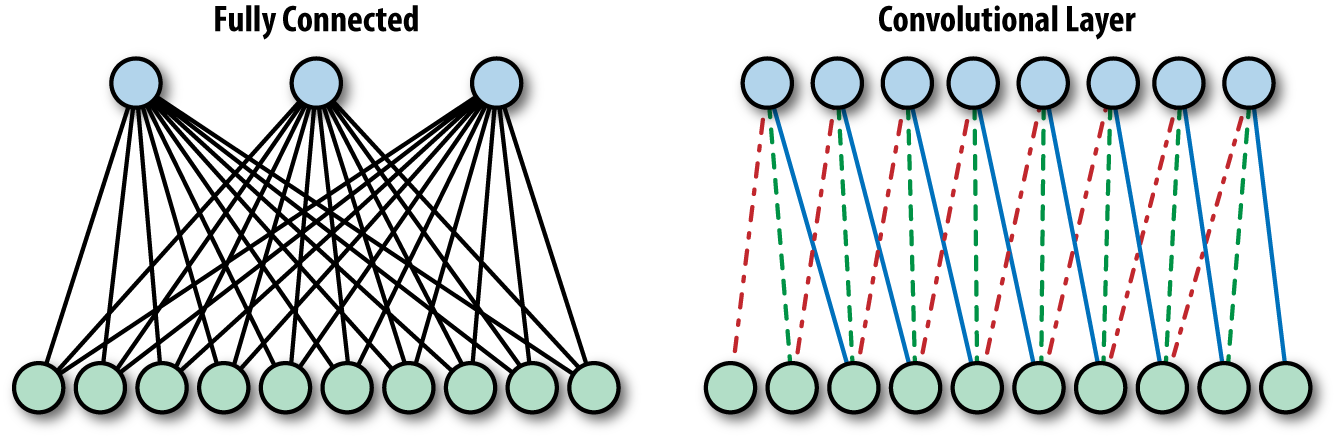
Figure 4-1. In a fully connected layer (left), each unit is connected to all units of the previous layers. In a convolutional layer (right), each unit is connected to a constant number of units in a local region of the previous layer. Furthermore, in a convolutional layer, the units all share the weights for these connections, as indicated by the shared linetypes.
There are motivations commonly cited as leading to the CNN approach, coming from different schools of thought. The first angle is the so-called neuroscientific inspiration behind the model. The second deals with insight into the nature of images, and the third relates to learning theory. We will go over each of these shortly before diving into the actual mechanics.
It has been popular to describe neural networks in general, and specifically convolutional neural networks, as biologically inspired models of computation. At times, claims go as far as to state that these mimic the way the brain performs computations. While misleading when taken at face value, the biological analogy is of some interest.
The Nobel Prize–winning neurophysiologists Hubel and Wiesel discovered as early as the 1960s that the first stages of visual processing in the brain consist of application of the same local filter (e.g., edge detectors) to all parts of the visual field. The current understanding in the neuroscientific community is that as visual processing proceeds, information is integrated from increasingly wider parts of the input, and this is done hierarchically.
Convolutional neural networks follow the same pattern. Each convolutional layer looks at an increasingly larger part of the image as we go deeper into the network. Most commonly, this will be followed by fully connected layers that in the biologically inspired analogy act as the higher levels of visual processing dealing with global information.
The second angle, more hard fact engineering–oriented, stems from the nature of images and their contents. When looking for an object in an image, say the face of a cat, we would typically want to be able to detect it regardless of its position in the image. This reflects the property of natural images that the same content may be found in different locations of an image. This is property is known as an invariance—invariances of this sort can also be expected with respect to (small) rotations, changing lighting conditions, etc.
Correspondingly, when building an object-recognition system, it should be invariant to translation (and, depending on the scenario, probably also rotation and deformations of many sorts, but that is another matter). Put simply, it therefore makes sense to perform the same exact computation on different parts of the image. In this view, a convolutional neural network layer computes the same features of an image, across all spatial areas.
Finally, the convolutional structure can be seen as a regularization mechanism. In this view, convolutional layers are like fully connected layers, but instead of searching for weights in the full space of matrices (of certain size), we limit the search to matrices describing fixed-size convolutions, reducing the number of degrees of freedom to the size of the convolution, which is typically very small.
Regularization
The term regularization is used throughout this book. In machine learning and statistics, regularization is mostly used to refer to the restriction of an optimization problem by imposing a penalty on the complexity of the solution, in the attempt to prevent overfitting to the given examples.
Overfitting occurs when a rule (for instance, a classifier) is computed in a way that explains the training set, but with poor generalization to unseen data.
Regularization is most often applied by adding implicit information regarding the desired results (this could take the form of saying we would rather have a smoother function, when searching a function space). In the convolutional neural network case, we explicitly state that we are looking for weights in a relatively low-dimensional subspace corresponding to fixed-size convolutions.
In this chapter we cover the types of layers and operations associated with convolutional neural networks. We start by revisiting the MNIST dataset, this time applying a model with approximately 99% accuracy. Next, we move on to the more interesting object recognition CIFAR10 dataset.
MNIST: Take II
In this section we take a second look at the MNIST dataset, this time applying a small convolutional neural network as our classifier. Before doing so, there are several elements and operations that we must get acquainted with.
Convolution
The convolution operation, as you probably expect from the name of the architecture, is the fundamental means by which layers are connected in convolutional neural networks. We use the built-in TensorFlow conv2d():
tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME')
Here, x is the data—the input image, or a downstream feature map obtained further along in the network, after applying previous convolution layers. As discussed previously, in typical CNN models we stack convolutional layers hierarchically, and feature map is simply a commonly used term referring to the output of each such layer. Another way to view the output of these layers is as processed images, the result of applying a filter and perhaps some other operations. Here, this filter is parameterized by W, the learned weights of our network representing the convolution filter. This is just the set of weights in the small “sliding window” we see in Figure 4-2.
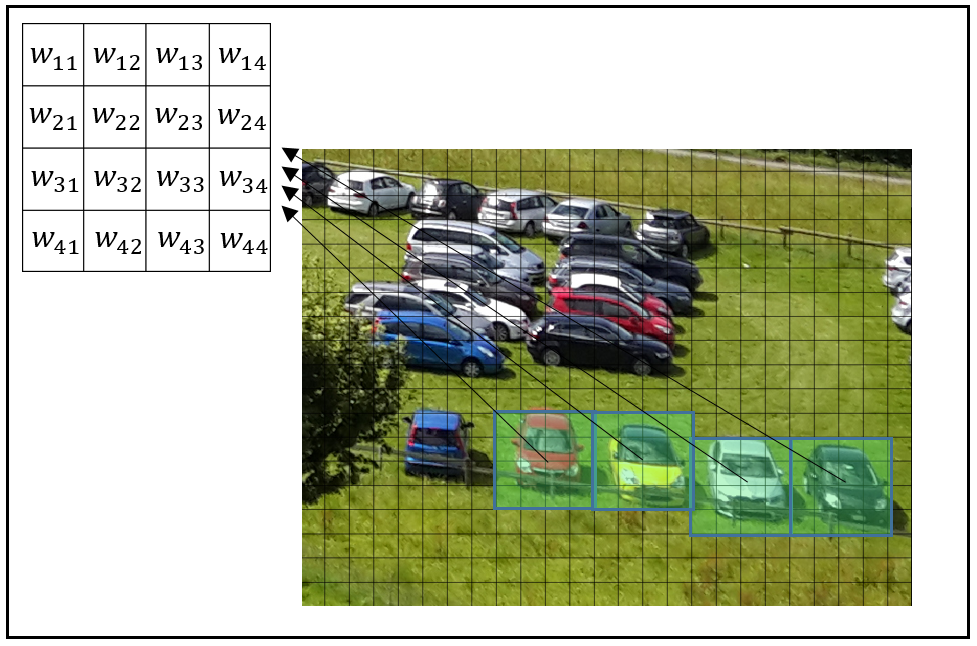
Figure 4-2. The same convolutional filter—a “sliding window”—applied across an image.
The output of this operation will depend on the shape of x and W, and in our case is four-dimensional. The image data x will be of shape:
[None, 28, 28, 1]
meaning that we have an unknown number of images, each 28×28 pixels and with one color channel (since these are grayscale images). The weights W we use will be of shape:
[5, 5, 1, 32]
where the initial 5×5×1 represents the size of the small “window” in the image to be convolved, in our case a 5×5 region. In images that have multiple color channels (RGB, as briefly discussed in Chapter 1), we regard each image as a three-dimensional tensor of RGB values, but in this one-channel data they are just two-dimensional, and convolutional filters are applied to two-dimensional regions. Later, when we tackle the CIFAR10 data, we’ll see examples of multiple-channel images and how to set the size of weights W accordingly.
The final 32 is the number of feature maps. In other words, we have multiple sets of weights for the convolutional layer—in this case, 32 of them. Recall that the idea of a convolutional layer is to compute the same feature along the image; we would simply like to compute many such features and thus use multiple sets of convolutional filters.
The strides argument controls the spatial movement of the filter W across the image (or feature map) x.
The value [1, 1, 1, 1] means that the filter is applied to the input in one-pixel intervals in each dimension, corresponding to a “full” convolution. Other settings of this argument allow us to introduce skips in the application of the filter—a common practice that we apply later—thus making the resulting feature map smaller.
Finally, setting padding to 'SAME' means that the borders of x are padded such that the size of the result of the operation is the same as the size of x.
Activation functions
Following linear layers, whether convolutional or fully connected, it is common practice to apply nonlinear activation functions (see Figure 4-3 for some examples). One practical aspect of activation functions is that consecutive linear operations can be replaced by a single one, and thus depth doesn’t contribute to the expressiveness of the model unless we use nonlinear activations between the linear layers.

Figure 4-3. Common activation functions: logistic (left), hyperbolic tangent (center), and rectifying linear unit (right)
Pooling
It is common to follow convolutional layers with pooling of outputs. Technically, pooling means reducing the size of the data with some local aggregation function, typically within each feature map.
The reasoning behind this is both technical and more theoretical. The technical aspect is that pooling reduces the size of the data to be processed downstream. This can drastically reduce the number of overall parameters in the model, especially if we use fully connected layers after the convolutional ones.
The more theoretical reason for applying pooling is that we would like our computed features not to care about small changes in position in an image. For instance, a feature looking for eyes in the top-right part of an image should not change too much if we move the camera a bit to the right when taking the picture, moving the eyes slightly to the center of the image. Aggregating the “eye-detector feature” spatially allows the model to overcome such spatial variability between images, capturing some form of invariance as discussed at the beginning of this chapter.
In our example we apply the max pooling operation on 2×2 blocks of each feature map:
tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
Max pooling outputs the maximum of the input in each region of a predefined size (here 2×2). The ksize argument controls the size of the pooling (2×2), and the strides argument controls by how much we “slide” the pooling grids across x, just as in the case of the convolution layer. Setting this to a 2×2 grid means that the output of the pooling will be exactly one-half of the height and width of the original, and in total one-quarter of the size.
Dropout
The final element we will need for our model is dropout. This is a regularization trick used in order to force the network to distribute the learned representation across all the neurons. Dropout “turns off” a random preset fraction of the units in a layer, by setting their values to zero during training. These dropped-out neurons are random—different for each computation—forcing the network to learn a representation that will work even after the dropout. This process is often thought of as training an “ensemble” of multiple networks, thereby increasing generalization. When using the network as a classifier at test time (“inference”), there is no dropout and the full network is used as is.
The only argument in our example other than the layer we would like to apply dropout to is keep_prob, the fraction of the neurons to keep working at each step:
tf.nn.dropout(layer,keep_prob=keep_prob)
In order to be able to change this value (which we must do, since for testing we would like this to be 1.0, meaning no dropout at all), we will use a tf.placeholder and pass one value for train (.5) and another for test (1.0).
The Model
First, we define helper functions that will be used extensively throughout this chapter to create our layers. Doing this allows the actual model to be short and readable (later in the book we will see that there exist several frameworks for greater abstraction of deep learning building blocks, which allow us to concentrate on rapidly designing our networks rather than the somewhat tedious work of defining all the necessary elements). Our helper functions are:
defweight_variable(shape):initial=tf.truncated_normal(shape,stddev=0.1)returntf.Variable(initial)defbias_variable(shape):initial=tf.constant(0.1,shape=shape)returntf.Variable(initial)defconv2d(x,W):returntf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME')defmax_pool_2x2(x):returntf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')defconv_layer(input,shape):W=weight_variable(shape)b=bias_variable([shape[3]])returntf.nn.relu(conv2d(input,W)+b)deffull_layer(input,size):in_size=int(input.get_shape()[1])W=weight_variable([in_size,size])b=bias_variable([size])returntf.matmul(input,W)+b
Let’s take a closer look at these:
weight_variable()-
This specifies the weights for either fully connected or convolutional layers of the network. They are initialized randomly using a truncated normal distribution with a standard deviation of .1. This sort of initialization with a random normal distribution that is truncated at the tails is pretty common and generally produces good results (see the upcoming note on random initialization).
bias_variable()-
This defines the bias elements in either a fully connected or a convolutional layer. These are all initialized with the constant value of
.1. conv2d()-
This specifies the convolution we will typically use. A full convolution (no skips) with an output the same size as the input.
max_pool_2×2-
This sets the max pool to half the size across the height/width dimensions, and in total a quarter the size of the feature map.
conv_layer()-
This is the actual layer we will use. Linear convolution as defined in
conv2d, with a bias, followed by the ReLU nonlinearity. full_layer()-
A standard full layer with a bias. Notice that here we didn’t add the ReLU. This allows us to use the same layer for the final output, where we don’t need the nonlinear part.
With these layers defined, we are ready to set up our model (see the visualization in Figure 4-4):
x=tf.placeholder(tf.float32,shape=[None,784])y_=tf.placeholder(tf.float32,shape=[None,10])x_image=tf.reshape(x,[-1,28,28,1])conv1=conv_layer(x_image,shape=[5,5,1,32])conv1_pool=max_pool_2x2(conv1)conv2=conv_layer(conv1_pool,shape=[5,5,32,64])conv2_pool=max_pool_2x2(conv2)conv2_flat=tf.reshape(conv2_pool,[-1,7*7*64])full_1=tf.nn.relu(full_layer(conv2_flat,1024))keep_prob=tf.placeholder(tf.float32)full1_drop=tf.nn.dropout(full_1,keep_prob=keep_prob)y_conv=full_layer(full1_drop,10)
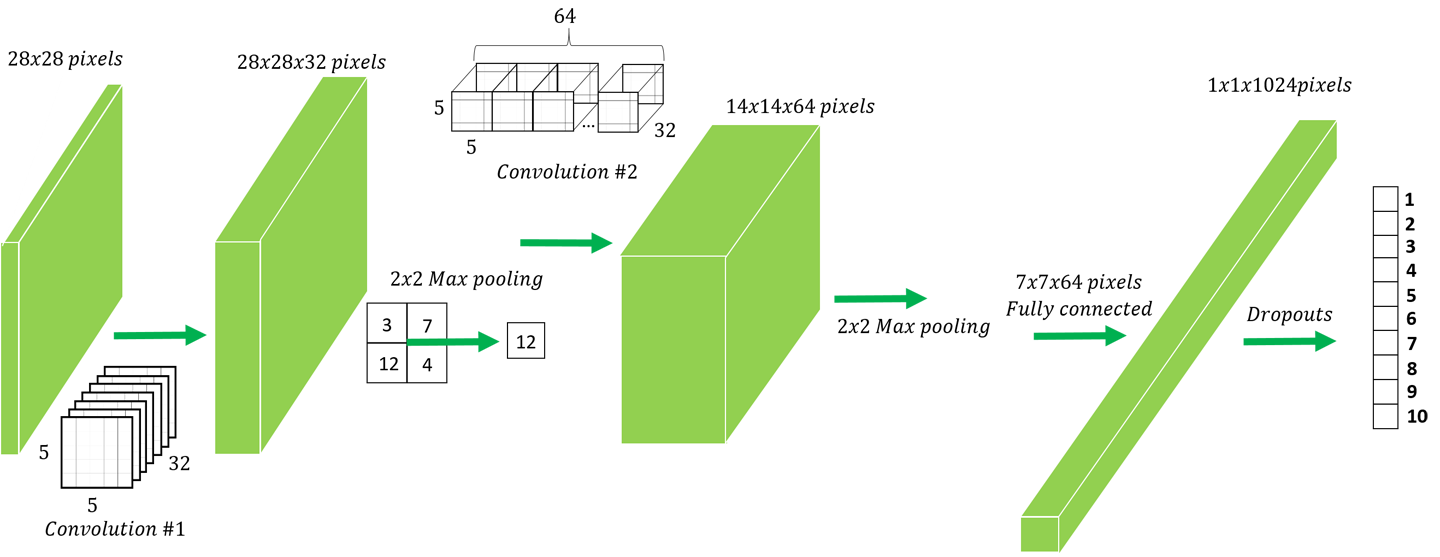
Figure 4-4. A visualization of the CNN architecture used.
Random initialization
In the previous chapter we discussed initializers of several types, including the random initializer used here for our convolutional layer’s weights:
initial = tf.truncated_normal(shape, stddev=0.1)
Much has been said about the importance of initialization in the training of deep learning models. Put simply, a bad initialization can make the training process “get stuck,” or fail completely due to numerical issues. Using random rather than constant initializations helps break the symmetry between learned features, allowing the model to learn a diverse and rich representation. Using bound values helps, among other things, to control the magnitude of the gradients, allowing the network to converge more efficiently.
We start by defining the placeholders for the images and correct labels, x and y_, respectively. Next, we reshape the image data into the 2D image format with size 28×28×1. Recall we did not need this spatial aspect of the data for our previous MNIST model, since all pixels were treated independently, but a major source of power in the convolutional neural network framework is the utilization of this spatial meaning when considering images.
Next we have two consecutive layers of convolution and pooling, each with 5×5 convolutions and 32 feature maps, followed by a single fully connected layer with 1,024 units. Before applying the fully connected layer we flatten the image back to a single vector form, since the fully connected layer no longer needs the spatial aspect.
Notice that the size of the image following the two convolution and pooling layers is 7×7×64. The original 28×28 pixel image is reduced first to 14×14, and then to 7×7 in the two pooling operations. The 64 is the number of feature maps we created in the second convolutional layer. When considering the total number of learned parameters in the model, a large proportion will be in the fully connected layer (going from 7×7×64 to 1,024 gives us 3.2 million parameters). This number would have been 16 times as large (i.e., 28×28×64×1,024, which is roughly 51 million) if we hadn’t used max-pooling.
Finally, the output is a fully connected layer with 10 units, corresponding to the number of labels in the dataset (recall that MNIST is a handwritten digit dataset, so the number of possible labels is 10).
The rest is the same as in the first MNIST model in Chapter 2, with a few minor changes:
train_accuracy-
We print the accuracy of the model on the batch used for training every 100 steps. This is done before the training step, and therefore is a good estimate of the current performance of the model on the training set.
test_accuracy-
We split the test procedure into 10 blocks of 1,000 images each. Doing this is important mostly for much larger datasets.
Here’s the complete code:
mnist=input_data.read_data_sets(DATA_DIR,one_hot=True)cross_entropy=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=y_conv,labels=y_))train_step=tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)correct_prediction=tf.equal(tf.argmax(y_conv,1),tf.argmax(y_,1))accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))withtf.Session()assess:sess.run(tf.global_variables_initializer())foriinrange(STEPS):batch=mnist.train.next_batch(50)ifi%100==0:train_accuracy=sess.run(accuracy,feed_dict={x:batch[0],y_:batch[1],keep_prob:1.0})"step {}, training accuracy {}".format(i,train_accuracy)sess.run(train_step,feed_dict={x:batch[0],y_:batch[1],keep_prob:0.5})X=mnist.test.images.reshape(10,1000,784)Y=mnist.test.labels.reshape(10,1000,10)test_accuracy=np.mean([sess.run(accuracy,feed_dict={x:X[i],y_:Y[i],keep_prob:1.0})foriinrange(10)])"test accuracy: {}".format(test_accuracy)
The performance of this model is already relatively good, with just over 99% correct after as little as 5 epochs,1 which are 5,000 steps with mini-batches of size 50.
For a list of models that have been used over the years with this dataset, and some ideas on how to further improve this result, take a look at http://yann.lecun.com/exdb/mnist/.
CIFAR10
CIFAR10 is another dataset with a long history in computer vision and machine learning. Like MNIST, it is a common benchmark that various methods are tested against. CIFAR10 is a set of 60,000 color images of size 32×32 pixels, each belonging to one of ten categories: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, and truck.
State-of-the-art deep learning methods for this dataset are as good as humans at classifying these images. In this section we start off with much simpler methods that will run relatively quickly. Then, we discuss briefly what the gap is between these and the state of the art.
Loading the CIFAR10 Dataset
In this section we build a data manager for CIFAR10, similarly to the built-in input_data.read_data_sets() we used for MNIST.2
First, download the Python version of the dataset and extract the files into a local directory. You should now have the following files:
- data_batch_1, data_batch_2, data_batch_3, data_batch_4, data_batch_5
- test_batch
- batches_meta
- readme.html
The data_batch_X files are serialized data files containing the training data, and test_batch is a similar serialized file containing the test data. The batches_meta file contains the mapping from numeric to semantic labels. The .html file is a copy of the CIFAR-10 dataset’s web page.
Since this is a relatively small dataset, we load it all into memory:
classCifarLoader(object):def__init__(self,source_files):self._source=source_filesself._i=0self.images=Noneself.labels=Nonedefload(self):data=[unpickle(f)forfinself._source]images=np.vstack([d["data"]fordindata])n=len(images)self.images=images.reshape(n,3,32,32).transpose(0,2,3,1)\.astype(float)/255self.labels=one_hot(np.hstack([d["labels"]fordindata]),10)returnselfdefnext_batch(self,batch_size):x,y=self.images[self._i:self._i+batch_size],self.labels[self._i:self._i+batch_size]self._i=(self._i+batch_size)%len(self.images)returnx,y
where we use the following utility functions:
DATA_PATH="/path/to/CIFAR10"defunpickle(file):withopen(os.path.join(DATA_PATH,file),'rb')asfo:dict=cPickle.load(fo)returndictdefone_hot(vec,vals=10):n=len(vec)out=np.zeros((n,vals))out[range(n),vec]=1returnout
The unpickle() function returns a dict with fields data and labels, containing the image data and the labels, respectively. one_hot() recodes the labels from integers (in the range 0 to 9) to vectors of length 10, containing all 0s except for a 1 at the position of the label.
Finally, we create a data manager that includes both the training and test data:
classCifarDataManager(object):def__init__(self):self.train=CifarLoader(["data_batch_{}".format(i)foriinrange(1,6)]).load()self.test=CifarLoader(["test_batch"]).load()
Using Matplotlib, we can now use the data manager in order to display some of the CIFAR10 images and get a better idea of what is in this dataset:
defdisplay_cifar(images,size):n=len(images)plt.figure()plt.gca().set_axis_off()im=np.vstack([np.hstack([images[np.random.choice(n)]foriinrange(size)])foriinrange(size)])plt.imshow(im)plt.show()d=CifarDataManager()"Number of train images: {}".format(len(d.train.images))"Number of train labels: {}".format(len(d.train.labels))"Number of test images: {}".format(len(d.test.images))"Number of test images: {}".format(len(d.test.labels))images=d.train.imagesdisplay_cifar(images,10)
Matplotlib
Matplotlib is a useful Python library for plotting, designed to look and behave like MATLAB plots. It is often the easiest way to quickly plot and visualize a dataset.
The display_cifar()function takes as arguments images (an iterable containing images), and size (the number of images we would like to display), and constructs and displays a size×size grid of images. This is done by concatenating the actual images vertically and horizontally to form a large image.
Before displaying the image grid, we start by printing the sizes of the train/test sets. CIFAR10 contains 50K training images and 10K test images:
Numberoftrainimages:50000Numberoftrainlabels:50000Numberoftestimages:10000Numberoftestimages:10000
The image produced and shown in Figure 4-5 is meant to give some idea of what CIFAR10 images actually look like. Notably, these small, 32×32 pixel images each contain a full single object that is both centered and more or less recognizable even at this resolution.

Figure 4-5. 100 random CIFAR10 images.
Simple CIFAR10 Models
We will start by using the model that we have previously used successfully for the MNIST dataset. Recall that the MNIST dataset is composed of 28×28-pixel grayscale images, while the CIFAR10 images are color images with 32×32 pixels. This will necessitate minor adaptations to the setup of the computation graph:
cifar=CifarDataManager()x=tf.placeholder(tf.float32,shape=[None,32,32,3])y_=tf.placeholder(tf.float32,shape=[None,10])keep_prob=tf.placeholder(tf.float32)conv1=conv_layer(x,shape=[5,5,3,32])conv1_pool=max_pool_2x2(conv1)conv2=conv_layer(conv1_pool,shape=[5,5,32,64])conv2_pool=max_pool_2x2(conv2)conv2_flat=tf.reshape(conv2_pool,[-1,8*8*64])full_1=tf.nn.relu(full_layer(conv2_flat,1024))full1_drop=tf.nn.dropout(full_1,keep_prob=keep_prob)y_conv=full_layer(full1_drop,10)cross_entropy=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv,y_))train_step=tf.train.AdamOptimizer(1e-3).minimize(cross_entropy)correct_prediction=tf.equal(tf.argmax(y_conv,1),tf.argmax(y_,1))accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))deftest(sess):X=cifar.test.images.reshape(10,1000,32,32,3)Y=cifar.test.labels.reshape(10,1000,10)acc=np.mean([sess.run(accuracy,feed_dict={x:X[i],y_:Y[i],keep_prob:1.0})foriinrange(10)])"Accuracy: {:.4}%".format(acc*100)withtf.Session()assess:sess.run(tf.global_variables_initializer())foriinrange(STEPS):batch=cifar.train.next_batch(BATCH_SIZE)sess.run(train_step,feed_dict={x:batch[0],y_:batch[1],keep_prob:0.5})test(sess)
This first attempt will achieve approximately 70% accuracy within a few minutes (using a batch size of 100, and depending naturally on hardware and configurations). Is this good? As of now, state-of-the-art deep learning methods achieve over 95% accuracy on this dataset,3 but using much larger models and usually many, many hours of training.
There are a few differences between this and the similar MNIST model presented earlier. First, the input consists of images of size 32×32×3, the third dimension being the three color channels:
x=tf.placeholder(tf.float32,shape=[None,32,32,3])
Similarly, after the two pooling operations, we are left this time with 64 feature maps of size 8×8:
conv2_flat=tf.reshape(conv2_pool,[-1,8*8*64])
Finally, as a matter of convenience, we group the test procedure into a separate function called test(), and we do not print training accuracy values (which can be added back in using the same code as in the MNIST model).
Once we have a model with some acceptable baseline accuracy (whether derived from a simple MNIST model or from a state-of-the-art model for some other dataset), a common practice is to try to improve it by means of a sequence of adaptations and changes, until reaching what is necessary for our purposes.
In this case, leaving all the rest the same, we will add a third convolution layer with 128 feature maps and dropout. We will also reduce the number of units in the fully connected layer from 1,024 to 512:
x=tf.placeholder(tf.float32,shape=[None,32,32,3])y_=tf.placeholder(tf.float32,shape=[None,10])keep_prob=tf.placeholder(tf.float32)conv1=conv_layer(x,shape=[5,5,3,32])conv1_pool=max_pool_2x2(conv1)conv2=conv_layer(conv1_pool,shape=[5,5,32,64])conv2_pool=max_pool_2x2(conv2)conv3=conv_layer(conv2_pool,shape=[5,5,64,128])conv3_pool=max_pool_2x2(conv3)conv3_flat=tf.reshape(conv3_pool,[-1,4*4*128])conv3_drop=tf.nn.dropout(conv3_flat,keep_prob=keep_prob)full_1=tf.nn.relu(full_layer(conv3_drop,512))full1_drop=tf.nn.dropout(full_1,keep_prob=keep_prob)y_conv=full_layer(full1_drop,10)
This model will take slightly longer to run (but still way under an hour, even without sophisticated hardware) and achieve an accuracy of approximately 75%.
There is still a rather large gap between this and the best known methods. There are several independently applicable elements that can help close this gap:
- Model size
-
Most successful methods for this and similar datasets use much deeper networks with many more adjustable parameters.
- Additional types of layers and methods
-
Additional types of popular layers are often used together with the layers presented here, such as local response normalization.
- Optimization tricks
-
More about this later!
- Domain knowledge
-
Pre-processing utilizing domain knowledge often goes a long way. In this case that would be good old-fashioned image processing.
- Data augmentation
-
Adding training data based on the existing set can help. For instance, if an image of a dog is flipped horizontally, then it is clearly still an image of a dog (but what about a vertical flip?). Small shifts and rotations are also commonly used.
- Reusing successful methods and architectures
-
As in most engineering fields, starting from a time-proven method and adapting it to your needs is often the way to go. In the field of deep learning this is often done by fine-tuning pretrained models.
The final model we will present in this chapter is a smaller version of the type of model that actually produces great results for this dataset. This model is still compact and fast, and achieves approximately 83% accuracy after ~150 epochs:
C1,C2,C3=30,50,80F1=500conv1_1=conv_layer(x,shape=[3,3,3,C1])conv1_2=conv_layer(conv1_1,shape=[3,3,C1,C1])conv1_3=conv_layer(conv1_2,shape=[3,3,C1,C1])conv1_pool=max_pool_2x2(conv1_3)conv1_drop=tf.nn.dropout(conv1_pool,keep_prob=keep_prob)conv2_1=conv_layer(conv1_drop,shape=[3,3,C1,C2])conv2_2=conv_layer(conv2_1,shape=[3,3,C2,C2])conv2_3=conv_layer(conv2_2,shape=[3,3,C2,C2])conv2_pool=max_pool_2x2(conv2_3)conv2_drop=tf.nn.dropout(conv2_pool,keep_prob=keep_prob)conv3_1=conv_layer(conv2_drop,shape=[3,3,C2,C3])conv3_2=conv_layer(conv3_1,shape=[3,3,C3,C3])conv3_3=conv_layer(conv3_2,shape=[3,3,C3,C3])conv3_pool=tf.nn.max_pool(conv3_3,ksize=[1,8,8,1],strides=[1,8,8,1],padding='SAME')conv3_flat=tf.reshape(conv3_pool,[-1,C3])conv3_drop=tf.nn.dropout(conv3_flat,keep_prob=keep_prob)full1=tf.nn.relu(full_layer(conv3_drop,F1))full1_drop=tf.nn.dropout(full1,keep_prob=keep_prob)y_conv=full_layer(full1_drop,10)
This model consists of three blocks of convolutional layers, followed by the fully connected and output layers we have already seen a few times before. Each block of convolutional layers contains three consecutive convolutional layers, followed by a single pooling and dropout.
The constants C1, C2, and C3 control the number of feature maps in each layer of each of the convolutional blocks, and the constant F1 controls the number of units in the fully connected layer.
After the third block of convolutional layers, we use an 8×8 max pool layer:
conv3_pool=tf.nn.max_pool(conv3_3,ksize=[1,8,8,1],strides=[1,8,8,1],padding='SAME')
Since at this point the feature maps are of size 8×8 (following the first two poolings that each reduced the 32×32 pictures by half on each axis), this globally pools each of the feature maps and keeps only the maximal value. The number of feature maps at the third block was set to 80, so at this point (following the max pooling) the representation is reduced to only 80 numbers. This keeps the overall size of the model small, as the number of parameters in the transition to the fully connected layer is kept down to 80×500.
Summary
In this chapter we introduced convolutional neural networks and the various building blocks they are typically made of. Once you are able to get small models working properly, try running larger and deeper ones, following the same principles. While you can always have a peek in the latest literature and see what works, a lot can be learned from trial and error and figuring some of it out for yourself. In the next chapters, we will see how to work with text and sequence data and how to use TensorFlow abstractions to build CNN models with ease.
1 In machine learning and especially in deep learning, an epoch refers to a single pass over all the training data; i.e., when the learning model has seen each training example exactly one time.
2 This is done mostly for the purpose of illustration. There are existing open source libraries containing this sort of data wrapper built in, for many popular datasets. See, for example, the datasets module in Keras (keras.datasets), and specifically keras.datasets.cifar10.
3 See Who Is the Best in CIFAR-10? for a list of methods and associated papers.
Get Learning TensorFlow now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

