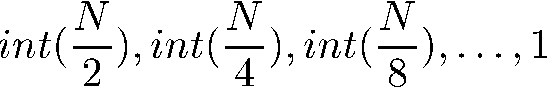Chapter 4. Sorting
The Librarian had seen many weird things in histime,butthathadtobethe57thstrangest. [footnote:hehadatidymind]
Sorting—the act of comparing and rearranging a collection of items—is one of the most important tasks computers perform. Sorting crops up everywhere; whenever you have a collection of items that need to be processed in a particular order, sorting helps you do it quickly.
In this chapter, we will explain what sorting is, how to do it
efficiently using Perl’s own
sort function, what comparing
actually means, and how you can code your own sort algorithms with
Perl.
An Introduction to Sorting
Sorting seems so simple. Novices don’t see why it should be difficult, and experts know that there are canned solutions that work very well. Nevertheless, there are tips that will speed up your sorts, and traps that will slow them down. We’ll explore them in this section. But first, the basics.
As in the two previous chapters, we’ll use addresses for our demonstrations. Addresses are an ideal choice, familiar to everyone while complex enough to demonstrate the most sophisticated attributes of data structures and algorithms.
On to sorting terminology. The items to be sorted are called records; the parts of those items used to determine the order are called keys or sometimes fields. The difference is subtle. Sometimes the keys are the records themselves, but sometimes they are just pieces of the records. Sometimes there is more than one key.
Consider three records from a telephone book:
Munro, Alice 15 Brigham Road 623-2448 Munro, Alice 48 Hammersley Place 489-1073 Munro, Alicia 62 Evergreen Terrace 623-6099
The last names are the primary keys because they are the first criterion for ordering entries. When two people have the same last name, the first names must be considered; those are the secondary keys. In the example above, even that isn’t enough, so we need tertiary keys: the street addresses. The rest of the data is irrelevant to our sort and is often called satellite data: here, the phone numbers. The index of this book contains primary and secondary keys, and an occasional tertiary key. The page numbers are satellite data.
We will explore several different sorting techniques in this
chapter. Some are worse (usually
time) than others (usually
time). Some perform much
better on certain input; others work well regardless of the input.
However, you may never need any of them, because Perl supplies you
with a very fast built-in function: sort(). We will
explore it first because we can use it to demonstrate what you need to
think about when orchestrating a sort operation. The important thing
to remember is that sort is
often—but not always—the best possible solution.
Perl’s sort Function
Under the hood, Perl’s sort() function uses the
quicksort
algorithm, which we’ll describe later in the chapter. This is a
standard sorting algorithm, provided by most operating systems as
qsort(3).[12]
In Versions 5.004_05 and higher, Perl uses its own quicksort
implementation instead of the one provided by the operating system.
Two primary motivations were behind this change. First, the
implementation has been highly optimized for Perl’s particular uses.
Second, some vendors’ implementations are buggy and cause errant
behavior, sometimes even causing programs to crash.
sort accepts two parameters: a sorting routine and
the list of items to sort. The sorting routine can be expressed
as a block of code or the name of a subroutine defined elsewhere
in the program, or you can omit it altogether. If you do provide a sorting
routine, it’s faster to provide it as a block than as a subroutine.
Here’s how to provide a subroutine:
@sorted = sort my_comparison @array;
sub my_comparison {
if ( $a > $b ) { return 1 }
elsif ( $b > $a ) { return -1 }
else { return 0 }
}Here’s the same operation, but with the sorting routine expressed as a block:
@sorted = sort { if ( $a > $b ) { return 1 }
elsif ( $b > $a ) { return -1 }
else { return 0 } } @array;
Each of these code snippets places a
copy of @array in
@sorted, sorted by the criterion we expressed
in the sorting routine. The original @array is
unchanged.
Every sorting routine, whether it’s a subroutine or an actual block,
is implicitly given two special variables: $a and
$b. These are the items to be compared. Don’t
modify them, ever. They are passed by reference, so changing them
changes the actual list elements. Changing $a and
$b midsort works about as well as changing your
tires mid-drive.
The sorting routine must return a number meeting these criteria:
If
$ais less than$b, the return value should be less than zero.If
$ais greater than than$b, the return value should be greater than zero.If
$ais equal to$b, the return value should be exactly zero.
As we hinted at before, the sorting routine is optional:
@sorted = sort @array;
This sorts @array in ASCII
order, which is sometimes what you want—not always.
ASCII Order
Perl’s default comparison rule is ASCII ordering.[13] Briefly, this means:
control characters< most punctuation< numbers< uppercase letters< lowercase letters
The complete ASCII table is available in Appendix B.
Numeric Order
ASCII order won’t help you to sort numbers. You’ll be unpleasantly surprised if you attempt the following:
@array = qw( 1234 +12 5 -3 ); @sorted = sort @array; print "sorted = @sorted\n";
This produces the strange result:
sorted = +12 -3 1234 5
This is a correct ASCII ordering.
ASCII order is very methodical: it always
looks at the keys one character at a time, starting from the
beginning. As soon as differing ASCII values for
those characters are found, the comparison rule is applied. For
example, when comparing 1234 to
5, 1234 is smaller because
1 is less than 5. That’s one of
the three reasons why ASCII is bad for comparing
numbers:
Numbers can start with a
+or-. They can also have anefollowed by another+or-, or nothing at all, and then some digits. Perl numbers can even have underscores in them to facilitate legibility: one million can be written as1000000or1e6or+1e+6or1_000_000.If you’re going to look at numbers character-by-character, then you need to look at all of the digits. Quick, which is bigger,
1345978066354223549678or926534216574835246783?Length isn’t good either:
4is bigger than3.14, which is bigger than5e-100.
Fortunately, it’s easy to have Perl sort things in numeric order. You
can just subtract $b from $a,
or use the more efficient Perl operator designed specifically for
comparing numbers: the so-called spaceship operator,
<=>.
You can sort numbers as follows:
@sorted_nums = sort { $a <=> $b } @unsorted;We can use the <=> operator in our example,
as follows:
@array = qw(1234 +12 5 -3);
@sorted_nums = sort { $a <=> $b } @array;
print "sorted_nums = @sorted_nums\n";This produces the result we want:
sorted_nums = -3 5 +12 1234
Reverse Order: From Highest To Lowest
To sort an array from highest to lowest, just flip
$a and $b. To order an array of
words from highest ASCII value to lowest, you can
say:
@words = sort { $b cmp $a } @words;cmp is Perl’s string comparison operator, the
counterpart of the numerical comparison operator,
<=>.
To sort an array of numbers from highest to lowest:
@numbers = sort { $b <=> $a } @numbers;
These examples also demonstrate something we haven’t yet seen: replacing
an array with a sorted copy of itself. We’ve done away with the @sorted variable and simply stored the results in the original
array.
Sort::Fields
If you don’t want to concoct your own sorting routines, you might be able to use Joseph N. Hall’s Sort::Fields module, available from CPAN. With it you can say convoluted things like “alphabetic sort on column 4, a numeric sort on column 1, and finally a reverse numeric sort on column 3.” You’d express this as follows:
use Sort::Fields; print fieldsort [4, '1n', '-3n'], @data;
The alphabetic sort is an ASCII sort—unless
you include the use locale statement, which we’ll
discuss shortly.
fieldsort() is just a wrapper for the module’s
make_fieldsort() function, which returns a subroutine:
use Sort::Fields; my $sort = make_fieldsort [4, '1n', '-3n']; print $sort->( @data );
If you are going to perform several Sort::Fields
operations using the same sorting rules, use
make_fieldsort() directly because
fieldsort() will call it each time. It’s faster to
create the sorting subroutine once and reuse it later than to create
it anew each time you call fieldsort().
The module also has stable versions of these
functions: stable_fieldsort() and
make_stable_fieldsort(). We’ll discuss
stability in Section 4.2.
Sort::Versions
Software version numbers don’t sort like regular numbers. There can be several fields, separated by dots. The fields might also have letters. For example:
1a 1.1 1.2 1.2a 1.2.1 1.2.a 1.2.b 1.03
The module Sort::Versions, by
Kenneth Albanowski, provides two subroutines:
versions() and versioncmp().
The former is used as a sorting routine, the latter as a general
function for comparing two Perl scalars as version numbers:
use Sort::Versions; @releases = sort versions qw( 2.3 2.4 2.3.1 2.3.0 2.4b ); print "earlier" if versioncmp( "3.4", "3.4a" ) == -1;
Note: if you use underscores to enhance the readability of your
“numbers”, like 5.004_05,
you need to remove the underscores before attempting a numeric
comparison.
An aside about underscores: Perl recognizes and removes them
only from literal numbers at compile time. If
you say perl -e "print 1_000_000", Perl prints
1000000. However, Perl won’t do the same for
strings: The underscores in $version = "5.004_05"
stay put. So for sorting version numbers, you’ll want to remove them:
@releases = sort versions map { tr/_//d; $_ } @array;This is a nuisance, but it’s necessary for backward compatibility: if Perl suddenly started parsing numbers after the underscore, thousands of existing scripts would break.
Dictionary Order
Dictionary order is another commonly used ordering. The strings are first transformed by removing everything except letters and numbers. Uppercase and lowercase variants are considered equal. These rules make words like re-evaluate, reevaluating, and Reevaluator sort close together. In ASCII order, they would be widely separated:
Reevaluator Rembrandt ... Zorro ... chthonic ... re-evaluate rectangle ... reevaluating
The difficulties don’t end here. In telephone books, finding people with names like De Lorean is troublesome. Is that under D or L? Similarly for abbreviations: should they be sorted according to the abbreviation itself or by the full name? Does IBM go between IAA and ICA or between Immigration and Ionization?
Further confusion arises from variations in spelling: Munro/Monroe, MacTavish/McTavish, Krysztof/Christoph, Peking/Beijing. In principle it would be nice to be able to find each pair at the same place when searching; a way to do this is shown in Section 9.3.1 in Chapter 9. Accommodating such a complicated criterion might introduce extra keys into the records—the primary key might even not be part of the original record at all!
Yet more fun occurs when the elements contain multibyte characters. In the world of ASCII, this never happens: every character takes up one byte. But in, say, Spanish, ch is a letter of its own, to be sorted between c and d: so chocolate follows color.[14] The international Unicode standard and Asian legacy standards define several different multibyte encodings. Especially nasty from the sorting viewpoint are those that have variable widths. For more information about different character encodings, see http://www.unicode.org/and http://www.czyborra.com/.
A simple version (that doesn’t handle quirky names, abbreviations, or
letters) for dictionary order sorting follows. Remember,
$a and $b must never ever be
modified, so we make “dictionary versions” of the
items to be compared: $da and
$db.
@dictionary_sorted =
sort {
my $da = lc $a; # Convert to lowercase.
my $db = lc $b;
$da =~ s/\W+//g; # Remove all nonalphanumerics.
$db =~ s/\W+//g;
$da cmp $db; # Compare.
} @array;There are at least two problems with the preceding code, however. They aren’t bugs, since the above sorting routine works correctly—sometimes.
Sorting Efficiency
The preceding program runs very slowly on long lists.
Unnecessarily slowly.
The problem is that the sorting routine is called every time two
elements need to be compared. The same elements will enter the
sorting routine several times, sometimes as $a and
sometimes as $b. This in turn means that the
transformation to the dictionary version will be
performed again and again for each word, even though we should only
need to do it once. Let’s illustrate this with a sort routine:
my @sorted =
sort { my $cmp = $a cmp $b;
$saw{ $a }++;
$saw{ $b }++;
print "a = $a, b = $b, cmp = $cmp, ",
"a is ",
$cmp < 0 ?
"smaller" : ( $cmp > 0 ? "bigger" : "equal" ),
" ",
$cmp ? "than" : "to", " b",
"\n";
return $cmp
} qw(you can watch what happens);
foreach ( sort keys %saw ) {
print "$_ $saw{ $_ } times\n";
}This displays the following:
a = you, b = can, cmp = 1, a is bigger than b a = you, b = watch, cmp = 1, a is bigger than b a = can, b = watch, cmp = -1, a is smaller than b a = you, b = what, cmp = 1, a is bigger than b a = watch, b = what, cmp = -1, a is smaller than b a = you, b = happens, cmp = 1, a is bigger than b a = what, b = happens, cmp = 1, a is bigger than b a = watch, b = happens, cmp = 1, a is bigger than b a = can, b = happens, cmp = -1, a is smaller than b can 3 times happens 4 times watch 4 times what 3 times you 4 times
Every word is compared three or four times. If our list were larger, there would have been even more comparisons per word. For large lists or a computationally expensive sorting routine, the performance degradation is substantial.
There is a Perl trick for avoiding the unnecessary work: the Schwartzian Transform, named after Randal Schwartz. The basic idea of the Schwartzian Transform is this: take the list to be sorted and create a second list combining both the original value and a transformed value to be used for the actual sorting. After the sort, the new value is thrown away, leaving only the elements of the original list.[15]
The Schwartzian Transform is described in more detail later in this chapter, but here is some dictionary sorting code that uses it. Thanks to the transform, the dictionary order transformation is performed only once for each word.
use locale;
# Fill @array here.
@dictionary_sorted =
map { $_->[0] }
sort { $a->[1] cmp $b->[1] }
map {
my $d = lc; # Convert into lowercase.
$d =~ s/[\W_]+//g; # Remove nonalphanumerics.
[ $_, $d ] # [original, transformed]
}
@array;In this particular case we can do even better and eliminate the anonymous lists. Creating and accessing them is slow compared to handling strings, so this will speed up our code further:
use locale;
@dictionary_sorted =
map { /^\w* (.*)/ }
sort
map {
my $d = lc; # Convert into lowercase.
$d =~ s/[\W_]+//g; # Remove nonalphanumerics.
"$d $_" # Concatenate new and original words.
}
@array;We transform the original strings into new strings containing both the transformed version and the original version. Then we sort on those transformed strings, and finally snip off the sorting keys and the space in between them, leaving only the original strings. However, this technique only works under these conditions:
You have to be able to produce sort keys that sort correctly with string comparison. Integers work only if you add leading spaces or zeros to align them on the right.
You have to able to stringify and later destringify the data—the stringification must be exactly reversible. Floating point numbers and objects need not apply.
You have to able to decouple the transformed sort key from the original data: in our sort, we did this by first destroying all
[\W_]characters and then using such a character, the space, as a separator.
Now our dictionary sort is robust, accurate, and fast.
The Schwartzian Transform
The Schwartzian Transform is a cache technique that lets you perform the time-consuming preprocessing stage of a sort only once. You can think of the Transform as a nested series of operations, modeled in Figure 4-1.
The
map function transforms one
list into another, element by element. We’ll use
@array = qw(opal-shaped opalescent Opalinidae);
as the list and the dictionary transformation from the previous section:
my $d = lc; # Convert into lowercase. $d =~ s/[\W_]+//g; [ $_, $d ]
so that the Schwartzian Transform in our case looks like Figure 4-2.
As the first step in the operation, the list to be sorted:
is transformed into another list by the
innermost (rightmost) map:
The old words are on the left; the new list is on the right. The actual sort is then performed using the new transformed list, on the right:[16]
However, the desired sort results are the plain old elements, not
these intermediate lists. These elements are retrieved by peeling
away the now-useless transformed words with the outermost
(leftmost) map:
This is what ends up in @sorted.
Long duration caching
The Schwartzian Transform caches only for the duration of one
sort. If you’re going to sort the same elements
several times but with different orderings or with different
subselections of the elements, you can use a different strategy for
even greater savings: the sort keys can be precomputed and stored in a
separate data structure, such as an array or hash:
# Initialize the comparison cache.
%sort_by = ();
foreach $word ( @full_list ) {
$sort_by{ $word } =
some_complex_time_consuming_function($word);
}
The %sort_by hash can then be used like this:
@sorted_list =
sort
{ $sort_by{ $a } <=> $sort_by{ $b } }
@partial_list;This technique, computing derived values and storing them for later use, is called memoizing. The Memoize module, by Mark-Jason Dominus, described briefly in Section 1.2.5 in Chapter 1, is available on CPAN.
Deficiency: missing internationalization (locales)
ASCII contains the 26 letters familiar to U.S. readers, but not their exotic relatives:
déjà vu façade naïve Schrödinger
You can largely blame computers for why you don’t often see the ï
of naïve: for a long time, support for “funny
characters” was nonexistent. However, writing foreign words
and names correctly is a simple matter of courtesy. The graphical
differences might seem insignificant but then again, so are the
differences between 0 and O, or 1 and l. When spoken,
a and ä may have completely
different sounds, and the meanings of words can change when letters
are replaced with an ASCII substitute. For
example, stripping the diaereses from Finnish
säästää (“to
save”) leaves saastaa
(“filth”).
These multicultural hardships are alleviated in part by
locales.
A locale is a set of rules represented by language-country-encoding triplet.
Locales are encoded as strings, for example
fr_CA.ISO8859-1 for
French-Canadian-ISO Latin 1.[17]
The rules specify things like which characters are letters and how
they should be sorted.
Earlier, we mentioned how multibyte characters can impact naïve sorting. Even single byte characters can present obstacles; for example, in Swedish å is sorted after z, and nowhere near a.
One way to refer to an arbitrary alphanumeric character regardless of
locale is with the Perl regular expression metacharacter
\w. And even that isn’t quite right because
\w includes _. The reason for
this is historical: _ is often used in computers as
if it were a true letter, as parts of names that are really phrases,
like_this. A rule of thumb is that \w
matches Perl identifiers; [A-Z] matches only
a range of 26 ASCII letters.
Even if we use \w, Perl still won’t treat the funny
letters as true characters. The actual way of telling Perl to
understand such letters is a long and system-dependent story. Please
see the perllocale documentation bundled with Perl
for details. For now, we’ll assume your operating system has locale
support installed and that your own personal locale setup is correct.
If so, all Perl needs is the locale pragma placed near the beginning
of your script:
use locale;
This tells Perl to use your locale environment to decide which characters are letters and how to order them, among other things. We can update our sorting program to handle locales as follows:
use locale;
# Fill @array here...
@dictionary_sorted =
sort {
my $da = lc $a; # Translate into lowercase.
my $db = lc $b;
$da =~ s/[\W_]+//g; # Remove all nonalphanumerics.
$db =~ s/[\W_]+//g;
$da cmp $db; # Compare.
} @array;
print "@dictionary_sorted";Sort::ArbBiLex
Often, vendor-supplied locales are lacking, broken, or completely missing. In this case, the Sort::ArbBiLex module by Sean M. Burke comes in handy. It lets you construct arbitrary bi-level lexicographic sort routines that specify in great detail how characters and character groups should be sorted. For example:
use Sort::ArbBiLex;
*Swedish_sort = Sort::ArbBiLex::maker(
"a A
o O
ä Ä
ö Ö
"
);
*German_sort = Sort::ArbBiLex::maker(
"a A
ä Ä
o O
ö Ö
"
);
@words = qw(Möller Märtz Morot Mayer Mortenson Mattson);
foreach (Swedish_sort(@words)) { print "på svenska: $_\n" }
foreach (German_sort (@words)) { print "auf Deutsch: $_\n" }This prints:
på svenska: Mayer på svenska: Mattson på svenska: Morot på svenska: Mortenson på svenska: Märtz på svenska: Möller auf Deutsch: Mayer auf Deutsch: Mattson auf Deutsch: Märtz auf Deutsch: Morot auf Deutsch: Mortenson auf Deutsch: Möller
Notice how Märtz and Möller are sorted differently.
See for yourself: use the Benchmark module
How substantial are the savings of the Schwartzian Transform?
You can measure phenomena like this yourself with the Benchmark
module (see Section 1.2.2 in
Chapter 1 for more
information). We will use Benchmark::timethese() to
benchmark with and without the Schwartzian Transform:
use Benchmark;
srand; # Randomize.
# NOTE: for Perls < 5.004
# use srand(time + $$ + ($$ << 15)) for better results
# Generate a nice random input array.
@array = reverse 'aaa'..'zaz';
# Mutate the @array.
for ( @array ) {
if (rand() < 0.5) { # Randomly capitalize.
$_ = ucfirst;
}
if (rand() < 0.25) { # Randomly insert underscores.
substr($_, rand(length), 0)= '_';
}
if (rand() < 0.333) { # Randomly double.
$_ .= $_;
}
if (rand() < 0.333) { # Randomly mirror double.
$_ .= reverse $_;
}
if (rand() > 1/length) { # Randomly delete characters.
substr($_, rand(length), rand(length)) = '';
}
}
# timethese() comes from Benchmark.
timethese(10, {
'ST' =>
'@sorted =
map { $_->[0] }
sort { $a->[1] cmp $b->[1] }
map { # The dictionarization.
my $d = lc;
$d =~ s/[\W_]+//g;
[ $_, $d ]
}
@array',
'nonST' =>
'@sorted =
sort { my ($da, $db) = ( lc( $a ), lc( $b ) );
$da =~ s/[\W_]+//g;
$db =~ s/[\W_]+//g;
$da cmp $db;
}
@array'
});We generate a reasonably random input array for our test. In one particular machine,[18] this code produces the following:
Benchmark: timing 10 iterations of ST, nonST...
ST: 22 secs (19.86 usr 0.55 sys = 20.41 cpu)
nonST: 44 secs (43.08 usr 0.15 sys = 43.23 cpu)The Schwartzian Transform is more than twice as fast.
The Schwartzian Transform can transform more than strings. For instance, here’s how you’d sort files based on when they were last modified:
@modified =
map { $_->[0] }
sort { $a->[1] <=> $b->[1] }
# -M is when $_ was last modified
map { [ $_, -M ] }
@filenames;Sorting Hashes Is Not What You Might Think
There is no such thing as a sorted hash. To be
more precise: sorting a simple hash is unthinkable. However, you can
create a complex hash that allows for sorting with tie.
In Perl, it is possible to tie arrays and hashes so
that operations like storing and retrieving can trigger special
operations, such as maintaining order within a hash. One example is
the BTREE method
for sorted, balanced binary trees, available in the
DB_File module bundled with the Perl distribution and
maintained by
Paul Marquess, or the
Tie::IxHash module by
Gurusamy Sarathy available from CPAN.
But back to simple hashes: As you know, a hash is a list of key-value pairs. You can find a value by knowing its key—but not vice versa. The keys are unique; the values need not be. Let’s look at the bookshelf of a science fiction buff. Here are the number of books (the values) for each author (the keys):
%books = ("Clarke" => 20, "Asimov" => 25, "Lem" => 20);
You can walk through this hash in “hash order” with
Perl’s built-in keys, values,
and each operators, but that’s not really a sorted
hash. As was mentioned in Chapter 2, the internal hash ordering is
determined by Perl so that it can optimize retrieval. This order
changes dynamically as elements are added and deleted.
foreach $author ( sort keys %books ) {
print "author = $author, books = $books{$author}\n";
}You can also walk through the hash in the order of the values. But be careful, since the values aren’t guaranteed to be unique:
foreach $author ( sort { $books{ $a } <=> $books{ $b } } keys %books ) {
print "author = $author, ";
print "books = $books{$author}\n";
}As you can see, the keys aren’t sorted at all:
author = Lem, books = 20 author = Asimov, books = 20 author = Clarke, books = 25
We can make sort adjudicate ties (that is, when
<=> yields 0). When that happens, we’ll resort to
an alphabetical ordering (cmp) of the author names:
foreach $author ( sort {
my $numcmp = $books{ $a } <=> $books{ $b };
return $numcmp if $numcmp;
return $a cmp $b;
} keys %h ) {
print "author = $author, ";
print "books = $books{$author}\n";
}This outputs:
author = Asimov, books = 20 author = Lem, books = 20 author = Clarke, books = 25
Note that we didn’t do this: sort { $a <=> $b } values %books—and for a good reason: it would make no sense,
because there’s no way to retrieve the key given the value.
It is possible to “reverse” a hash, yielding a new hash where the keys become values and the values become keys. You can do that with hashes of lists or, more precisely, a hash of references to lists. We need lists because a given hash might not be a one-to-one mapping. If two different keys have the same value, it’s a one-to-many mapping.
%books = ("Clarke" => 20, "Asimov" => 25, "Lem" => 20);
%books_by_number = ();
while ( ($key, $value) = each %books ) {
push @{ $books_by_number{ $value } }, $key;
}
foreach $number ( sort { $a <=> $b } keys %books_by_number ) {
print "number = $number, ";
print "authors = @{ $books_by_number{ $number } }\n";
}This displays:
number = 20, authors = Clarke Lem number = 25, authors = Asimov
After all this talk about the trickiness involved in sorting hashes,
prepare yourself for the horror that occurs if you mistakenly try to
sort a hash directly. Had we tried %torn_books = sort %books; we end up with this:
Clarke => 'Lem', 20 => 20, 25 => 'Asimov'
Clarke has written “Lem” books, and 25 has written “Asimov” books?
So don’t do that.
All Sorts of Sorts
Perl’s own sort is very fast, and it’s useful to
know why it’s fast—and when it’s
not. Eventually, you’ll stumble upon situations in which you can improve
performance by using some of the algorithms in this section.
Here, we compare several families of sorting algorithms and describe
the situations in which you’ll want to use them. The guiding light
for choosing an algorithm is this: the more you know about your
data, the better.
Sorting algorithms can scale well or poorly. An algorithm scales well
when the running time of the sort doesn’t increase much as the number
of elements increases. A poorly scaling algorithm is typically
: when the
number of elements doubles, the running time quadruples. For sorting,
“scaling well” usually means ; we’ll call this
log-linear.
In addition to their running times, sorting algorithms can be categorized by their stability and sensitivity. Stability refers to the fate of records with identical keys: a stable algorithm preserves their original order, while an unstable algorithm might not. Stability is a good thing, but it’s not vital; often we’ll want to sacrifice it for speed.
Sensitive algorithms are volatile.[19] They react strongly (either very well or very poorly) to certain kinds of input data. Sensitive sorting algorithms that normally perform well might perform unexpectedly poorly on some hard-to-predict random order or a nearly sorted order or a reversed order. For some algorithms, the order of input does not matter as much as the distribution of the input. Insensitive algorithms are better because they behave more predictably.
In the remainder of this chapter all the algorithms sort
strings. If you want numeric sorting, change the
string operators to their numeric equivalents: gt
should become >, eq should
become ==, and so on. Alternatively, the
subroutines could be
implemented in a more general (but slower) way to accept a sorting
routine as a parameter.
Unlike Perl’s sort, most of these algorithms sort
arrays
in place (also known as
in situ),
operating directly on their arguments instead of making copies. This
is a major benefit if the arrays are large because there’s no need to
store both the original array and the sorted one; you get an instant
50% savings in memory consumption. This also means you should provide
your list as an array reference, not as a regular array.
Passing references to subroutines avoids copying the array and is
therefore faster.
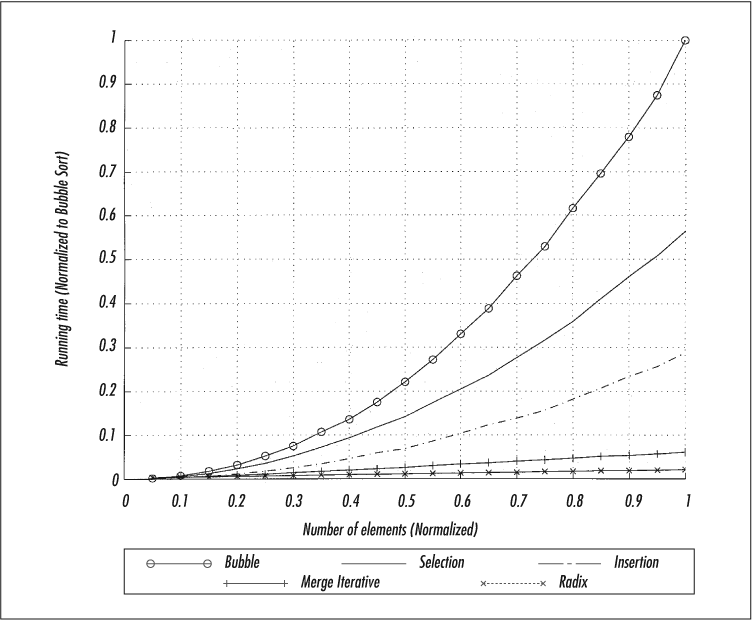
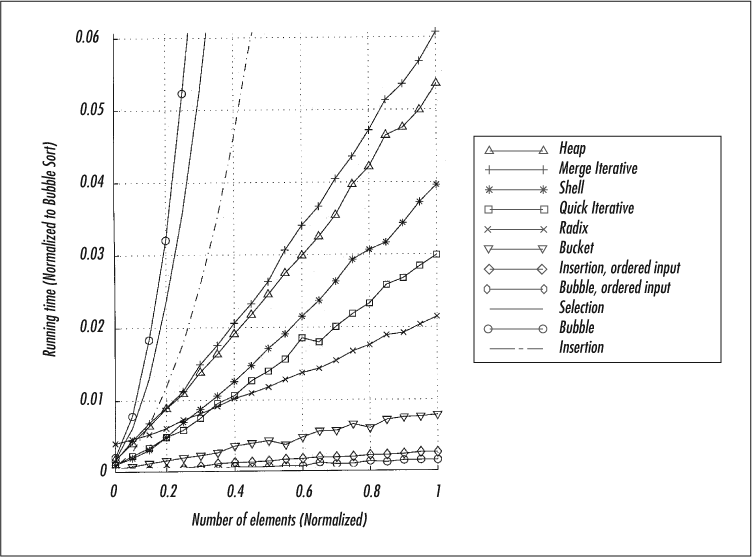
We show graphs that compare the performance of these sorting techniques at the end of the chapter.
Quadratic Sorting Algorithms
Here we present the three most basic sorting algorithms. They also happen to be the three worst techniques for the typical use: sorting random data. The first of these three algorithms, selection sort, fares quite poorly as a general sorting algorithm but is good for finding the minimum and maximum of unordered data.
The next two quadratic sorts, bubble sort and insertion sort, are also poor choices for random data, but in certain situations they are the fastest of all.
If there are constraints in how data can be moved around, these two sorts might be the best choices. An analogy of this would be moving heavy boxes around or moving the armature of a jukebox to select the appropriate CD. In these cases, the cost of moving elements is very high.
Selection sort
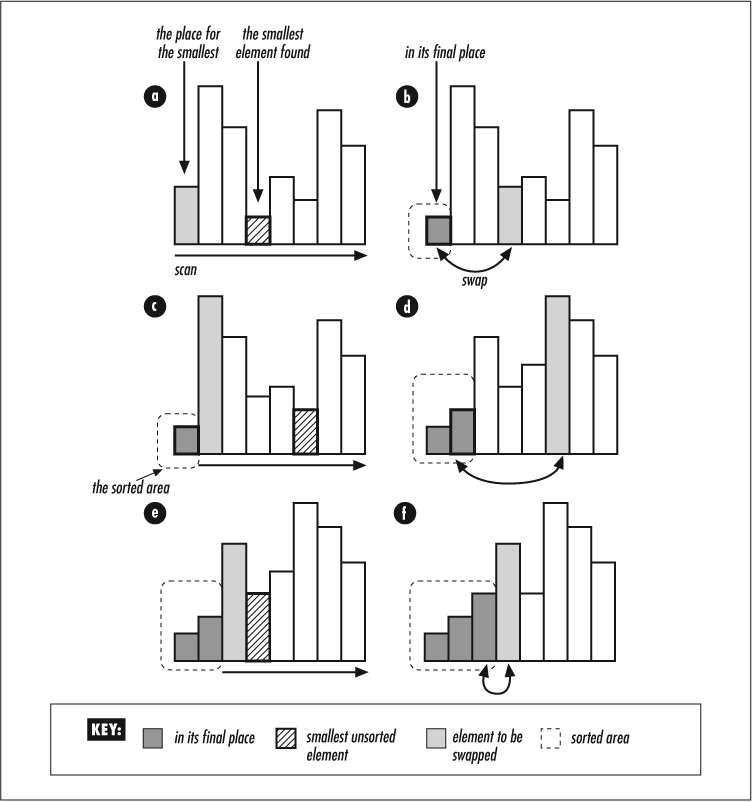
The selection sort is the simplest sorting algorithm. Find the smallest element and put it in the appropriate place. Lather. Rinse. Repeat.
Figure 4-3 illustrates selection sort. The unsorted part of the array is scanned (as shown by the horizontal line), and the smallest element is swapped with the lowest element in that part of the array (as shown by the curved lines.) Here’s how it’s implemented for sorting strings:
sub selection_sort {
my $array = shift;
my $i; # The starting index of a minimum-finding scan.
my $j; # The running index of a minimum-finding scan.
for ( $i = 0; $i < $#$array ; $i++ ) {
my $m = $i; # The index of the minimum element.
my $x = $array->[ $m ]; # The minimum value.
for ( $j = $i + 1; $j < @$array; $j++ ) {
( $m, $x ) = ( $j, $array->[ $j ] ) # Update minimum.
if $array->[ $j ] lt $x;
}
# Swap if needed.
@$array[ $m, $i ] = @$array[ $i, $m ] unless $m == $i;
}
}We can invoke selection_sort() as follows:
@array = qw(able was i ere i saw elba); selection_sort(\@array); print "@array\n";
able elba ere i i saw was Don’t use selection sort as a general-purpose sorting algorithm. It’s
dreadfully slow—
—which is a pity because
it’s both stable and insensitive.
A short digression: pay particular attention to the last line in
selection_sort(), where we use array slices to swap
two elements in a single statement.
Minima and maxima
The selection sort finds the minimum value and moves it into place,
over and over. If all you want is the minimum (or the maximum) value
of the array, you don’t need to sort the the rest of the values—you
can just loop through the elements, a
procedure. On the other
hand, if you want to find the extremum multiple times in a rapidly
changing data collection, use a heap, described
in Section 3.8 in Chapter 3. Or, if you want a set of extrema
(“Give me the ten largest”), use the
percentile() function described in
Section 4.2.2.4 later in this chapter.
For unordered data, minimum() and
maximum() are simple to implement since all the
elements must be scanned.
A more difficult issue is which comparison to use. Usually, the
minimum and the maximum would be needed for numerical data; here, we
provide both numeric and string variants. The
s-prefixed versions are for string comparisons, and
the g-prefixed versions are generic: they take a
subroutine reference as their first parameter, and that subroutine is
used to compare the elements. The return value of the subroutine must
behave just like the comparison subroutine of sort:
a negative value if the first argument is less than the second, a
positive value if the first argument is greater than the second, and
zero if they are equal. One critical difference: because it’s a
regular subroutine, the arguments to be compared are
$_[0] and $_[1] and not
$a and $b.
The algorithms for the minimum are as follows:
sub min { # Numbers.
my $min = shift;
foreach ( @_ ) { $min = $_ if $_ < $min }
return $min;
}
sub smin { # Strings.
my $s_min = shift;
foreach ( @_ ) { $s_min = $_ if $_ lt $s_min }
return $smin;
}
sub gmin { # Generic.
my $g_cmp = shift;
my $g_min = shift;
foreach ( @_ ) { $g_min = $_ if $g_cmp->( $_, $g_min ) < 0 }
return $g_min;
}Here are the algorithms for the maximum:
sub max { # Numbers.
my $max = shift;
foreach ( @_ ) { $max = $_ if $_ > $max }
return $max;
}
sub smax { # Strings.
my $s_max = shift;
foreach ( @_ ) { $s_max = $_ if $_ gt $s_max }
return $s_max;
}
sub gmax { # Generic.
my $g_cmp = shift;
my $g_max = shift;
foreach ( @_ ) { $g_max = $_ if $g_cmp->( $_, $g_max ) > 0 }
return $g_max;
}In the generic subroutines, you’ll notice that we invoke the
user-provided subroutine as
$code_refererence->(arguments). That’s less
punctuation-intensive than the equivalent
&{$code_refererence}(arguments).
If you want to know which element contains the minimum instead of the actual value, we can do that as follows:
sub mini {
my $l = $_[ 0 ];
my $n = @{ $l };
return ( ) unless $n; # Bail out if no list is given.
my $v_min = $l->[ 0 ]; # Initialize indices.
my @i_min = ( 0 );
for ( my $i = 1; $i < $n; $i++ ) {
if ( $l->[ $i ] < $v_min ) {
$v_min = $l->[ $i ]; # Update minimum and
@i_min = ( $i ); # reset indices.
} elsif ( $l->[ $i ] == $v_min ) {
push @i_min, $i; # Accumulate minimum indices.
}
}
return @i_min;
}
sub maxi {
my $l = $_[ 0 ];
my $n = @{ $l };
return ( ) unless $n; # Bail out if no list is given.
my $v_max = $l->[ 0 ]; # Initialize indices.
my @i_max = ( 0 );
for ( my $i = 1; $i < $n; $i++ ) {
if ( $l->[ $i ] > $v_max ) {
$v_max = $l->[ $i ]; # Update maximum and
@i_max = ( $i ); # reset indices.
} elsif ( $l->[ $i ] == $v_max ) {
push @i_max, $i; # Accumulate maximum indices.
}
}
return @i_max;
}smini(), gmini(),
smaxi(), and gmaxi() can be
written similarly. Note that these functions should return
arrays of indices instead of a single index
since the extreme values might lie in several array locations:
# Index: 0 1 2 3 4 5 6 7 8 9 10 11 my @x = qw(31 41 59 26 59 26 35 89 35 89 79 32); my @i_max = maxi(\@x); # @i_max should now contain 7 and 9.
Lastly, we present a general extrema-finding subroutine. It uses a generic sorting routine and returns the minima- or maxima-holding indices:
sub gextri {
my $g_cmp = $_[ 0 ];
my $l = $_[ 1 ];
my $n = @{ $l };
return ( ) unless $n; # Bail out if no list is given.
my $v_min = $l->[ 0 ];
my $v_max = $v_min; # The maximum so far.
my @i_min = ( 0 ); # The minima indices.
my @i_max = ( 0 ); # The maxima indices.
my $v_cmp; # The result of comparison.
for ( my $i = 1; $i < $n; $i++ ) {
$v_cmp = $g_cmp->( $l->[ $i ], $v_min );
if ( $v_cmp < 0 ) {
$v_min = $l->[ $i ]; # Update minimum and reset minima.
@i_min = ( $i );
} elsif ( $v_cmp == 0 ) {
push @i_min, $i ; # Accumulate minima if needed.
} else { # Not minimum: maybe maximum?
$v_cmp = $g_cmp->( $l->[ $i ], $v_max );
if ( $v_cmp > 0 ) {
$v_max = $l->[ $i ]; # Update maximum and reset maxima.
@i_max = ( $i );
} elsif ( $v_cmp == 0 ) {
push @i_max, $i; # Accumulate maxima.
}
} # Else neither minimum nor maximum.
}
return ( \@i_min, \@i_max );
}This returns a list of two anonymous arrays (array references) containing the indices of the minima and maxima:
# 0 1 2 3 4 5 6 7 8 9 10 11
my @x = qw(31 41 59 26 59 26 35 89 35 89 79 32);
my ($i_min, $i_max) = gextri(sub { $_[0] <=> $_[1] }, \@x);
# @$i_min now contains 3 and 5.
# @$i_max now contains 7 and 9.Remember that the preceding extrema-finding subroutines make sense only for unordered data. They make only one linear pass over the data—but they do that each time they are called. If you want to search the data quickly or repeatedly, see Section 3.8 in Chapter 3.
Bubble sort
The bubble sort has the cutest and most descriptive name of all the sort algorithms—but don’t be tempted by a cute name.
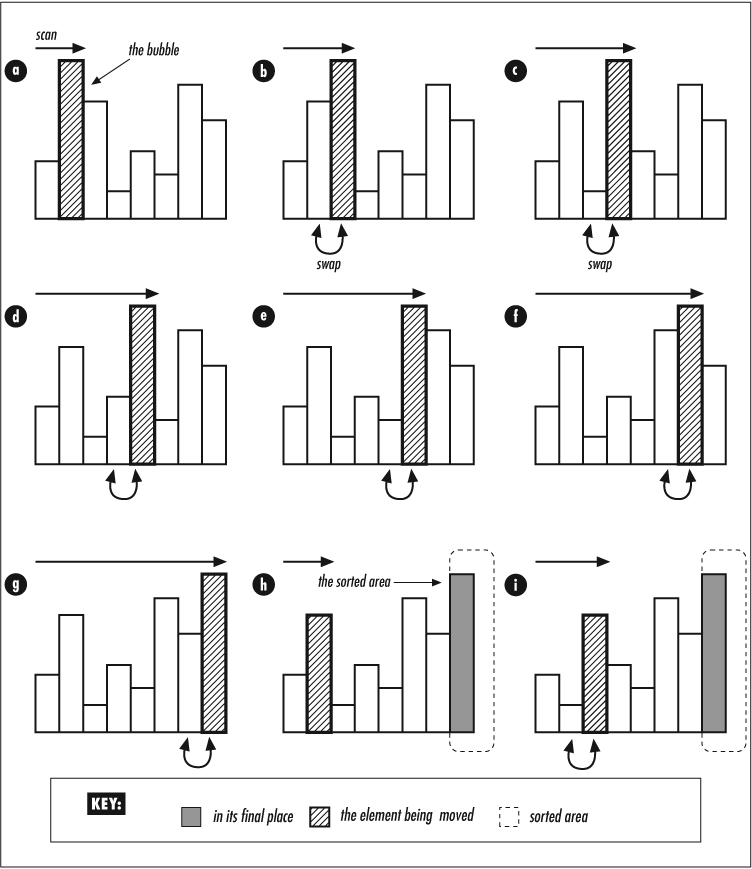
This sort makes multiple scans through the array, swapping adjacent pairs of elements if they’re in the wrong order, until no more swaps are necessary. If you follow an element as it propagates through the array, that’s the “bubble.”
Figure 4-4 illustrates the first full scan (stages a to g) and the first stages of the second scan (stages h and i).
sub bubblesort {
my $array = shift;
my $i; # The initial index for the bubbling scan.
my $j; # The running index for the bubbling scan.
my $ncomp = 0; # The number of comparisons.
my $nswap = 0; # The number of swaps.
for ( $i = $#$array; $i; $i-- ) {
for ( $j = 1; $j <= $i; $j++ ) {
$ncomp++;
# Swap if needed.
if ( $array->[ $j - 1 ] gt $array->[ $j ] ) {
@$array[ $j, $j - 1 ] = @$array[ $j - 1, $j ];
$nswap++;
}
}
}
print "bubblesort: ", scalar @$array,
" elements, $ncomp comparisons, $nswap swaps\n";
}We have included comparison and swap counters, $ncomp
and $nswap, for comparison with a variant
of this routine to be shown later. The later variant greatly reduces
the number of comparisons, especially if the input is sorted or almost sorted.
Avoid using bubble sort as a general-purpose sorting algorithm. Its
worst-case performance is 
, and its
average performance is one of the worst because it might traverse the
list as many times as there are elements. True, the unsorted part of
the list does get one element shorter each time, yielding the series
, but that’s still
.
However, bubble sort has a very interesting property: for fully or almost fully sorted data it is the fastest algorithm of all. It might sound strange to sort sorted data, but it’s a frequent situation: suppose you have a ranked list of sports teams. Whenever teams play, their ranks change—but not by much. The rankings are always nearly sorted. To reduce the left and right bounds of the sorted area more quickly when the data is already mostly sorted, we can use the following variant:
sub bubblesmart {
my $array = shift;
my $start = 0; # The start index of the bubbling scan.
my $ncomp = 0; # The number of comparisons.
my $nswap = 0; # The number of swaps.
my $i = $#$array;
while ( 1 ) {
my $new_start; # The new start index of the bubbling scan.
my $new_end = 0; # The new end index of the bubbling scan.
for ( my $j = $start || 1; $j <= $i; $j++ ) {
$ncomp++;
if ( $array->[ $j - 1 ] gt $array->[ $j ] ) {
@$array[ $j, $j - 1 ] = @$array[ $j - 1, $j ];
$nswap++;
$new_end = $j - 1;
$new_start = $j - 1 unless defined $new_start;
}
}
last unless defined $new_start; # No swaps: we're done.
$i = $new_end;
$start = $new_start;
}
print "bubblesmart: ", scalar @$array,
" elements, $ncomp comparisons, $nswap swaps\n";
}You can compare this routine and the original bubblesort with the following code:
@a = "a".."z";
# Reverse sorted, both equally bad.
@b = reverse @a;
# Few inserts at the end.
@c = ( @a, "a".."e" );
# Random shuffle.
srand();
foreach ( @d = @a ) {
my $i = rand @a;
( $_, $d[ $i ] ) = ( $d[ $i ], $_ );
}
my @label = qw(Sorted Reverse Append Random);
my %label;
@label{\@a, \@b, \@c, \@d} = 0..3;
foreach my $var ( \@a, \@b, \@c, \@d ) {
print $label[$label{$var}], "\n";
bubblesort [ @$var ];
bubblesmart [ @$var ];
}This will output the following (the number of comparisons at the last line will vary slightly):
Sorted bubblesort: 26 elements, 325 comparisons, 0 swaps bubblesmart: 26 elements, 25 comparisons, 0 swaps Reverse bubblesort: 26 elements, 325 comparisons, 325 swaps bubblesmart: 26 elements, 325 comparisons, 325 swaps Append bubblesort: 31 elements, 465 comparisons, 115 swaps bubblesmart: 31 elements, 145 comparisons, 115 swaps Random bubblesort: 26 elements, 325 comparisons, 172 swaps bubblesmart: 26 elements, 279 comparisons, 172 swaps
As you can see, the number of comparisons is lower with
bubblesmart() and significantly lower
for already sorted data. This reduction in the number
of comparisons does not come for free, of course: updating the start
and end indices consumes cycles.
For sorted data, the bubble sort runs in linear time,
, because it quickly realizes
that there is very little (if any) work to be done: sorted data
requires only a few swaps. Additionally, if the size if the array is
small, so is 
. There is
not a lot of work done in each of the
actions, so this can be faster
than an 
algorithm that
does more work for each of its steps. This feature makes bubble sort
very useful for hybrid
sorts, which we’ll encounter later in the chapter.
Insertion sort
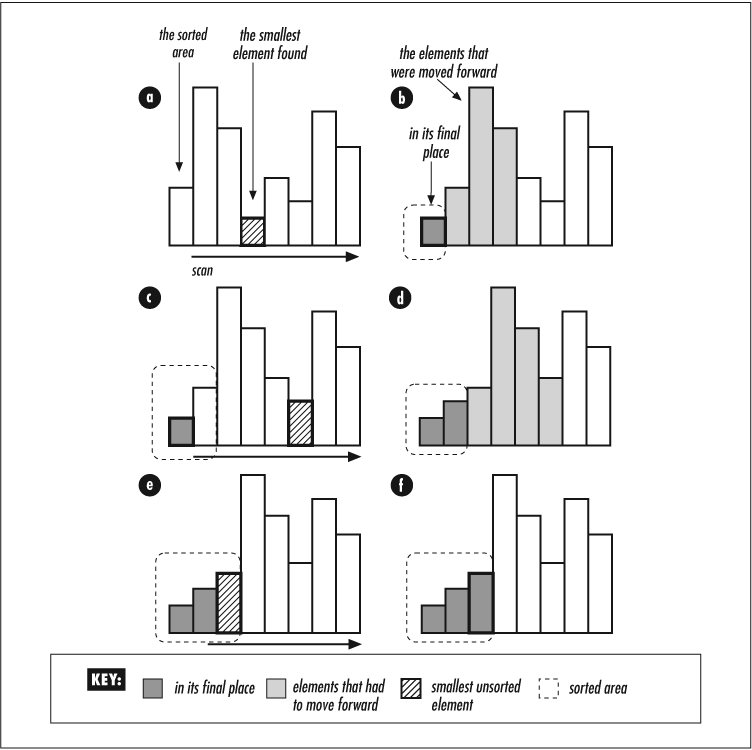
Insertion sort scans all elements, finds the smallest, and “inserts” it in its proper place. As each correct place is found, the remaining unsorted elements are shifted forward to make room, and the process repeats. A good example of insertion sort is inserting newly bought books into an alphabetized bookshelf. This is also the trick people use for sorting card hands: the cards are arranged according to their value one at a time.[20]
In Figure 4-5, steps
a, c, and e
find the minimums; steps b, d,
and e insert those minimums into their rightful
places in the array. insertion_sort() implements
the procedure:
sub insertion_sort {
my $array = shift;
my $i; # The initial index for the minimum element.
my $j; # The running index for the minimum-finding scan.
for ( $i = 0; $i < $#$array; $i++ ) {
my $m = $i; # The final index for the minimum element.
my $x = $array->[ $m ]; # The minimum value.
for ( $j = $i + 1; $j < @$array; $j++ ) {
( $m, $x ) = ( $j, $array->[ $j ] ) # Update minimum.
if $array->[ $j ] lt $x;
}
# The double-splice simply moves the $m-th element to be
# the $i-th element. Note: splice is O(N), not O(1).
# As far as the time complexity of the algorithm is concerned
# it makes no difference whether we do the block movement
# using the preceding loop or using splice(). Still, splice()
# is faster than moving the block element by element.
splice @$array, $i, 0, splice @$array, $m, 1 if $m > $i;
}
}
Do not use insertion sort as a general-purpose sorting algorithm. It has
worst-case, and its
average performance is one of the worst of the sorting algorithms
in this chapter. However, like bubble sort,
insertion sort is very fast for sorted or almost sorted
data—
—and for the same reasons. The
two sorting algorithms are actually very similar: bubble sort bubbles
large elements up through an unsorted area to the end, while insertion
sort bubbles elements down through a sorted area to the beginning.
The preceding insertion sort code is actually optimized for already sorted
data. If the $j loop were written like this:
for ( $j = $i;
$j > 0 && $array->[ --$j ] gt $small; ) { }
# $small is the minimum element
$j++ if $array->[ $j ] le $small;sorting random or reversed data would slightly speed up (by a couple of percentage points), while sorting already sorted data would slow down by about the same amount.
One hybrid situation is especially appropriate for insertion sort:
let’s say you have a large sorted array and you wish to add a small
number of elements to it. The best procedure here is to sort
the small group of newcomers and then merge them into the large array.
Because both arrays are sorted, this
insertion_merge() routine can merge them together
in one pass through the larger array:
sub insertion_merge {
my ( $large, $small ) = @_;
my $merge; # The merged result.
my $i; # The index to @merge.
my $l; # The index to @$large.
my $s; # The index to @$small.
$#$merge = @$large + @$small - 1; # Pre-extend.
for ( ($i, $l, $s) = (0, 0, 0); $i < @$merge; $i++ ) {
$merge->[ $i ] =
$l < @$large &&
( $s == @$small || $large->[ $l ] < $small->[ $s ] ) ?
$large->[ $l++ ] :
$small->[ $s++ ] ;
}
return $merge;
}
Here’s how we’d use insertion_merge() to
insert some primes into squares:
@large = qw( 1 4 9 16 25 36 49 64 81 100);@small = qw( 2 5 11 17 23);$merge = insertion_merge( \@large, \@small );print "@{$merge}\n";1 2 4 5 9 11 16 17 23 25 36 49 64 81 100
Shellsort
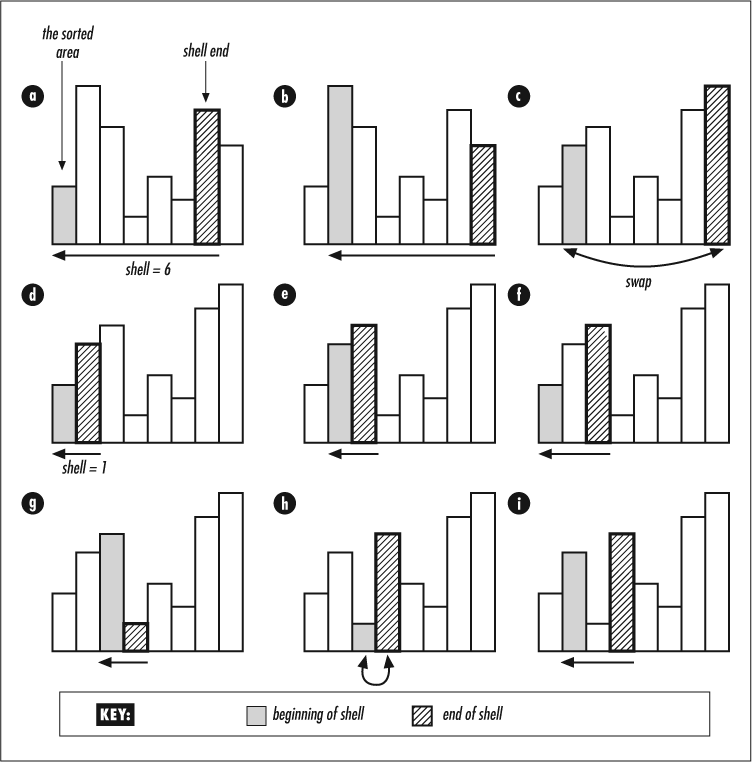
Shellsort is an advanced cousin of bubble sort. While bubble sort swaps only adjacent elements, shellsort swaps the elements over much longer distances. With each iteration, that distance shortens until it reaches one, and after that pass, the array is sorted. The distance is called the shell. The term isn’t so great a metaphor as one would hope; the sort is named after its creator, Donald Shell.
The shell spirals from the size of the array down to one element. That spiraling can happen via many paths. For instance, it might be this:
Or it might be this:
No series is always the best: the optimal series must be customized for each input. Of course, figuring that out might take as long as the sort, so it’s better to use a reasonably well-performing default. Besides, if we really knew the input intimately, there would be even better choices than shellsort. More about that in Section 4.2.3.
In our sample code we will calculate the shell by starting with
k
0 = 1
and repeatedly calculating
ki+1
= 2ki
+ 1
resulting in the series 1, 3, 7, 15, ....
We will use the series backwards, starting with the largest value
that is smaller than the size of the array, and ending with 1:
sub shellsort {
my $array = shift;
my $i; # The initial index for the bubbling scan.
my $j; # The running index for the bubbling scan.
my $shell; # The shell size.
my $ncomp = 0; # The number of comparisons.
my $nswap = 0; # The number of swaps.
for ( $shell = 1; $shell < @$array; $shell = 2 * $shell + 1 ) {
# Do nothing here, just let the shell grow.
}
do {
$shell = int( ( $shell - 1 ) / 2 );
for ( $i = $shell; $i < @$array; $i++ ) {
for ( $j = $i - $shell;
$j >= 0 && ++$ncomp &&
$array->[ $j ] gt $array->[ $j + $shell ];
$j -= $shell ) {
@$array[ $j, $j + $shell ] = @$array[ $j + $shell, $j ];
$nswap++;
}
}
} while $shell > 1;
print "shellsort: ", scalar @$array,
" elements, $ncomp comparisons, $nswap swaps\n";
}
If we test shellsort alongside the earlier bubblesort()
and bubblesmart() routines, we will
see results similar to:
Sorted bubblesort: 26 elements, 325 comparisons, 0 swaps bubblesmart: 26 elements, 25 comparisons, 0 swaps shellsort: 26 elements, 78 comparisons, 0 swaps Reverse bubblesort: 26 elements, 325 comparisons, 325 swaps bubblesmart: 26 elements, 325 comparisons, 325 swaps shellsort: 26 elements, 97 comparisons, 35 swaps Append bubblesort: 31 elements, 465 comparisons, 115 swaps bubblesmart: 31 elements, 145 comparisons, 115 swaps shellsort: 31 elements, 133 comparisons, 44 swaps Random bubblesort: 26 elements, 325 comparisons, 138 swaps bubblesmart: 26 elements, 231 comparisons, 138 swaps shellsort: 26 elements, 115 comparisons, 44 swaps
In Figure 4-6, the shell distance begins
at 6, and the innermost loop makes shell-sized hops backwards in the
array, swapping whenever needed. The shellsort()
subroutine implements this sort.
The average performance of shellsort is very good, but somewhat hard
to analyze; it is thought to be something like
, or possibly
.
The worst case is
.
The exact performance characteristics of shellsort are difficult to
analyze because they depend on the series chosen for
$shell.
Log-Linear Sorting Algorithms
In this section, we’ll explore some
sorts: mergesort, heapsort,
and quicksort.
Mergesort
Mergesort is a divide-and-conquer strategy (see Section 1.3 in Chapter 1). The “divide” step literally divides the array in half. The “conquer” is the merge operation: the halved arrays are recombined to form the sorted array.
To illustrate these steps, assume we have only two elements in each subarray. Either the elements are already in the correct order, or they must be swapped. The merge step scans those two already sorted subarrays (which can be done in linear time), and from the elements picks the smallest and places it in the result array. This is repeated until no more elements remain in the two subarrays. Then, on the next iteration, the resulting larger subarrays are merged, and so on. Eventually, all the elements are merged into one array:
sub mergesort {
mergesort_recurse ($_[0], 0, $#{ $_[0] });
}
sub mergesort_recurse {
my ( $array, $first, $last ) = @_;
if ( $last > $first ) {
local $^W = 0; # Silence deep recursion warning.
my $middle = int(( $last + $first ) / 2);
mergesort_recurse( $array, $first, $middle );
mergesort_recurse( $array, $middle + 1, $last );
merge( $array, $first, $middle, $last );
}
}
my @work; # A global work array.
sub merge {
my ( $array, $first, $middle, $last ) = @_;
my $n = $last - $first + 1;
# Initialize work with relevant elements from the array.
for ( my $i = $first, my $j = 0; $i <= $last; ) {
$work[ $j++ ] = $array->[ $i++ ];
}
# Now do the actual merge. Proceed through the work array
# and copy the elements in order back to the original array.
# $i is the index for the merge result, $j is the index in
# first half of the working copy, $k the index in the second half.
$middle = int(($first + $last) / 2) if $middle > $last;
my $n1 = $middle - $first + 1; # The size of the 1st half.
for ( my $i = $first, my $j = 0, my $k = $n1; $i <= $last; $i++ ) {
$array->[ $i ] =
$j < $n1 &&
( $k == $n || $work[ $j ] lt $work[ $k ] ) ?
$work[ $j++ ] :
$work[ $k++ ];
}
}
Notice how we silence warnings with local $^W = 0;.
Silencing warnings is bad etiquette, but currently that’s the only way
to make Perl stop groaning about the deep recursion of mergesort. If
a subroutine calls itself more than 100 times and Perl is run with the
-w switch, Perl gets worried and exclaims,
Deep recursion on subroutine .... The
-w switch sets the $^W to true;
we locally set it to false for the duration of the sort.
Mergesort is a very good sort algorithm. It scales well and is
insensitive to the key distribution of the input:
. This is obvious
because each merge is 
, and
repetitively halving 
elements takes
rounds. The bad news is
that the traditional implementation of mergesort requires additional
temporary space equal in size to the input array.
Mergesort’s recursion can be avoided easily by walking over the array with a working area that starts at 2 and doubles its size at each iteration. The inner loop does merges of the same size.
sub mergesort_iter ($) {
my ( $array ) = @_;
my $N = @$array;
my $Nt2 = $N * 2; # N times 2.
my $Nm1 = $N - 1; # N minus 1.
$#work = $Nm1;
for ( my $size = 2; $size < $Nt2; $size *= 2 ) {
for ( my $first = 0; $first < $N; $first += $size ) {
my $last = $first + $size - 1;
merge( $array,
$first,
int(($first + $last) / 2),
$last < $N ? $last : $Nm1 );
}
}
}
Heapsort
As its name suggests, the heapsort uses the heap data structure described in Section 3.8 in Chapter 3. In a sense, heapsort is similar to selection sort. It finds the largest element and moves it to the end. But the heap structure permits heapsort to avoid the expense of a full search to find each element, allowing the previously determined order to be used in subsequent passes.
use integer;.
sub heapify;
sub heapsort {
my $array = shift;
foreach ( my $index = 1 + @$array / 2; $index--; ) {
heapify $array, $index;
}
foreach ( my $last = @$array; --$last; ) {
@{ $array }[ 0, $last ] = @{ $array }[ $last, 0 ];
heapify $array, 0, $last;
}
}
sub heapify {
my ($array, $index, $last) = @_;
$last = @$array unless defined $last;
my $swap = $index;
my $high = $index * 2 + 1;
foreach ( my $try = $index * 2;
$try < $last && $try <= $high;
$try ++ ) {
$swap = $try if $array->[ $try ] gt $array->[ $swap ];
}
unless ( $swap == $index ) {
# The heap is in disorder: must reshuffle.
@{ $array }[ $swap, $index ] = @{ $array }[ $index, $swap ];
heapify $array, $swap, $last;
}
}
Heapsort is a nice overall algorithm. It is one of the fastest sorting
algorithms, it scales well, and it is insensitive, yielding
performance.
Furthermore, the first element is available in
time, and each subsequent
element takes time. If
you only need the first 
elements
of a set, in order, you can sort them in
time in general, and in
time if
is known in advance.
Heapsort is unstable, but for certain data structures, particularly those used in graph algorithms (see Chapter 8), it is the sorting algorithm of choice.
Quicksort
Quicksort is a well-known divide-and-conquer
algorithm. So
well-known, in fact, that Perl uses it for implementing its own
sort. Quicksort is a good compromise when
no characteristics of the input are known.
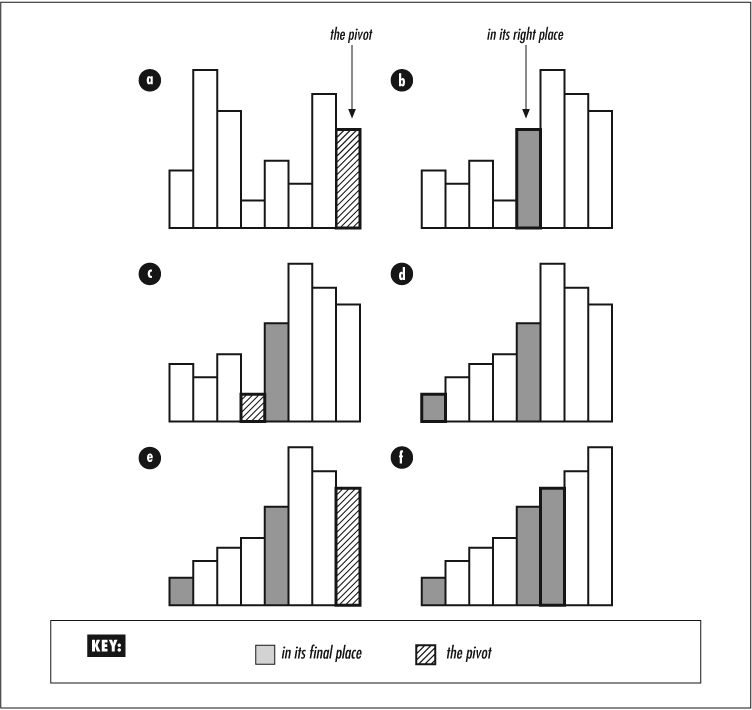
The basic idea is to pick one element of the array and shuffle it to its final place. That element is known as the pivot, and the shuffling is known as partitioning. The pivot divides the array into two partitions (at some points three; more about this shortly). These two partitions are then recursively quicksorted. A moderately good first guess for the pivot is the last element, but that can lead into trouble with certain input data, as we’ll see.
The partitioning does all the work of comparing and exchanging the elements. Two scans proceed in parallel, one from the beginning of the array and the other from the end. The first scan continues until an element larger than the pivot is found. The second scan continues until an element smaller than the pivot is found. If the scans cross, both stop. If none of the conditions terminating the scans are triggered, the elements at the first and second scan positions are exchanged. After the scans, we exchange the element at the first scan and the pivot.
The partitioning algorithm is as follows:
At Point 1 (see the
partition()subroutine) the elements in positions$first..$i-1are all less than or equal to the pivot, the elements in$j+1..$last-1are all greater than or equal to the pivot, and the element in$lastis equal to the pivot.At Point 2 the elements in
$first..$i-1are all less than or equal to the pivot, the elements in$j+1..$last-1are all greater than or equal to the pivot, the elements in$j+1..$i-1are all equal to the pivot, and the element at$lastis equal to the pivot.At Point 3 we have a three way partitioning. The first partition contains elements that are less than or equal to the pivot; the second partition contains elements that are all equal to the pivot. (There must be at least one of these—the original pivot element itself.) The third partition contains elements that are greater than or equal to the pivot. Only the first and third partitions need further sorting.
The quicksort algorithm is illustrated in Figure 4-7.
First, let’s look at the partition subroutine:
sub partition {
my ( $array, $first, $last ) = @_;
my $i = $first;
my $j = $last - 1;
my $pivot = $array->[ $last ];
SCAN: {
do {
# $first <= $i <= $j <= $last - 1
# Point 1.
# Move $i as far as possible.
while ( $array->[ $i ] le $pivot ) {
$i++;
last SCAN if $j < $i;
}
# Move $j as far as possible.
while ( $array->[ $j ] ge $pivot ) {
$j--;
last SCAN if $j < $i;
}
# $i and $j did not cross over, so swap a low and a high value.
@$array[ $j, $i ] = @$array[ $i, $j ];
} while ( --$j >= ++$i );
}
# $first - 1 <= $j < $i <= $last
# Point 2.
# Swap the pivot with the first larger element (if there is one).
if ( $i < $last ) {
@$array[ $last, $i ] = @$array[ $i, $last ];
++$i;
}
# Point 3.
return ( $i, $j ); # The new bounds exclude the middle.
}
You can think of the partitioning process as a filter: the pivot
introduces a little structure to the data by dividing the elements
into less-or-equal and greater-or-equal portions. After the
partitioning, the quicksort itself is quite simple. We again silence
the deep recursion warning, as we did in
mergesort().
sub quicksort_recurse {
my ( $array, $first, $last ) = @_;
if ( $last > $first ) {
my ( $first_of_last, $last_of_first, ) =
partition( $array, $first, $last );
local $^W = 0; # Silence deep recursion warning.
quicksort_recurse $array, $first, $last_of_first;
quicksort_recurse $array, $first_of_last, $last;
}
}
sub quicksort {
# The recursive version is bad with BIG lists
# because the function call stack gets REALLY deep.
quicksort_recurse $_[ 0 ], 0, $#{ $_[ 0 ] };
}The performance of the recursive version can be enhanced by turning recursion into iteration; see Section 4.2.2.3.1.
If you expect that many of your keys will be the same, try adding this
before the return in partition():
# Extend the middle partition as much as possible. ++$i while $i <= $last && $array->[ $i ] eq $pivot; --$j while $j >= $first && $array->[ $j ] eq $pivot;
This is the possible third partition we hinted at earlier.
On average, quicksort is a very good sorting algorithm. But not
always: if the input is fully or close to being fully sorted or
reverse sorted, the algorithms spends a lot of effort exchanging and
moving the elements. It becomes as slow as bubble sort on random
data: 
.
This worst case can be avoided most of the time by techniques such as
the
median-of-three:
Instead of choosing the last element as the pivot, sort the first,
middle, and last elements of the array, and then use the middle one.
Insert the following before
$pivot = $array->[ $last ] in
partition():
my $middle = int( ( $first + $last ) / 2 ); @$array[ $first, $middle ] = @$array[ $middle, $first ] if $array->[ $first ] gt $array->[ $middle ]; @$array[ $first, $last ] = @$array[ $last, $first ] if $array->[ $first ] gt $array->[ $last ]; # $array[$first] is now the smallest of the three. # The smaller of the other two is the middle one: # It should be moved to the end to be used as the pivot. @$array[ $middle, $last ] = @$array[ $last, $middle ] if $array->[ $middle ] lt $array->[ $last ];
Another well-known shuffling technique is simply to choose the
pivot randomly. This makes the worst case unlikely, and even if
it does occur, the next time we choose a different pivot, it will
be extremely unlikely that we again hit the worst case.
Randomization is easy; just insert this before
$pivot = $array->[ $last ]:
my $random = $first + rand( $last - $first + 1 ); @$array[ $random, $last ] = @$array[ $last, $random ];
With this randomization technique, any input gives an expected running
time of . We
can say the randomized running time of
quicksort is
.
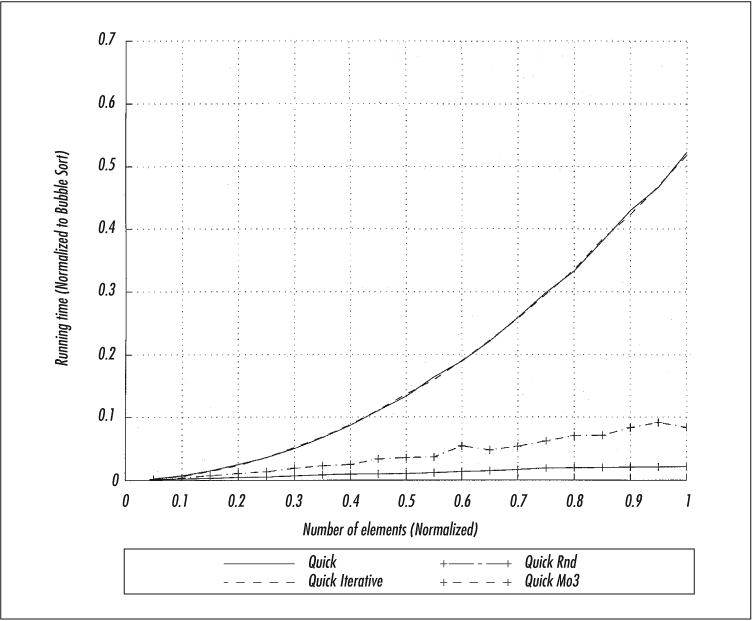
However, this is slower than median-of-three, as you’ll see in Figure 4-8 and Figure 4-9.
Removing recursion from quicksort
Quicksort uses a lot of stack space because it calls itself many times. You can avoid this recursion and save time by using an explicit stack. Using a Perl array for the stack is slightly faster than using Perl’s function call stack, which is what straightforward recursion would normally use:
sub quicksort_iterate {
my ( $array, $first, $last ) = @_;
my @stack = ( $first, $last );
do {
if ( $last > $first ) {
my ( $last_of_first, $first_of_last ) =
partition $array, $first, $last;
# Larger first.
if ( $first_of_last - $first > $last - $last_of_first ) {
push @stack, $first, $first_of_last;
$first = $last_of_first;
} else {
push @stack, $last_of_first, $last;
$last = $first_of_last;
}
} else {
( $first, $last ) = splice @stack, -2, 2; # Double pop.
}
} while @stack;
}
sub quicksort_iter {
quicksort_iterate $_[0], 0, $#{ $_[0] };
}
Instead of letting the quicksort subroutine call itself with the new
partition limits, we push the new limits onto a stack using
push and, when we’re done, pop the limits off the
stack with splice. An additional optimizing trick
is to push the larger of the two partitions onto the stack and process
the smaller partition first. This keeps @stack
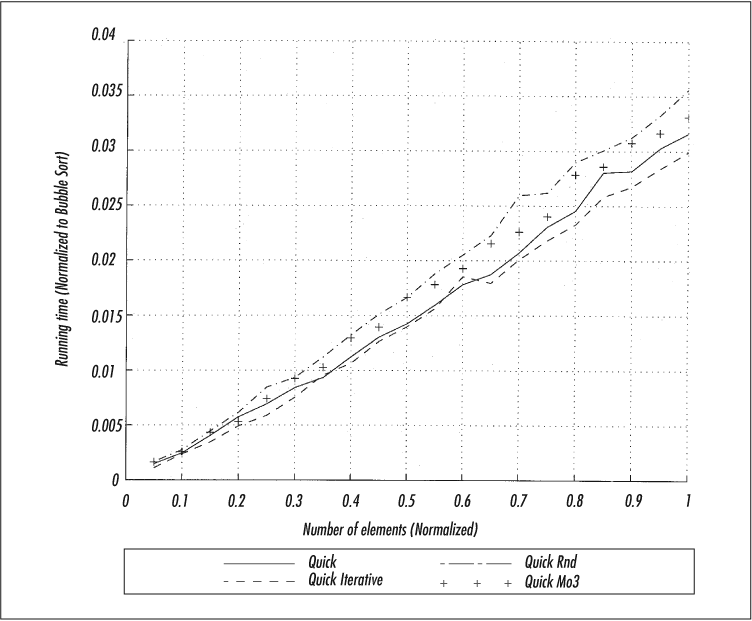
shallow. The effect is shown in Figure 4-8.
As you can see from Figure 4-8, these changes don’t help if you have random data. In fact, they hurt. But let’s see what happens with ordered data.
The enhancements in Figure 4-9 are quite striking. Without them, ordered data takes quadratic time; with them, the log-linear behavior is restored.
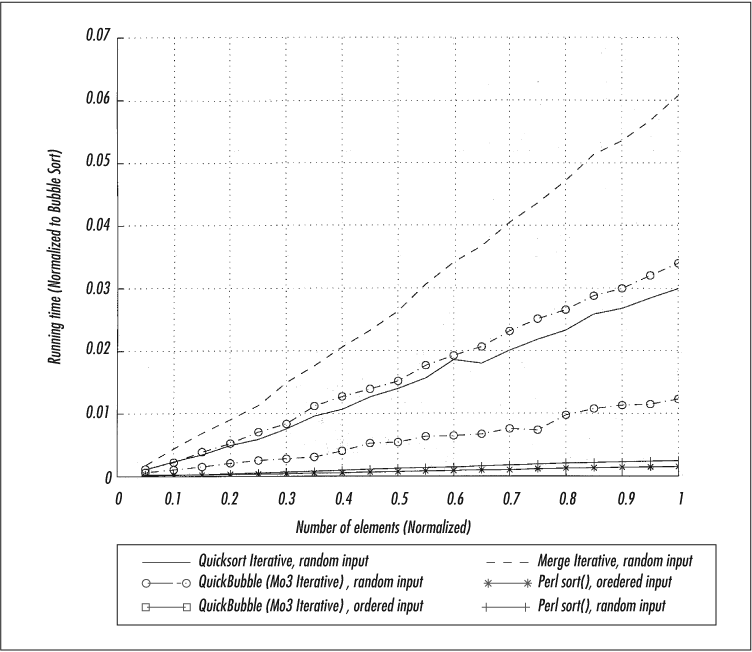
In Figure 4-8 and Figure 4-9, the x-axis is the number of records, scaled to 1.0. The y-axis is the relative running time, 1.0 being the time taken by the slowest algorithm (bubble sort). As you can see, the iterative version provides a slight advantage, and the two shuffling methods slow down the process a bit. But for already ordered data, the shuffling boosts the algorithm considerably. Furthermore, median-of-three is clearly the better of the two shuffling methods.
Quicksort is common in operating system and compiler libraries. As long as the code developers sidestepped the stumbling blocks we discussed, the worst case is unlikely to occur.
Quicksort is unstable: records having identical keys aren’t guaranteed to retain their original ordering. If you want a stable sort, use mergesort.
Median, quartile, percentile
A common task in statistics is finding the median of the input data. The median is the element in the middle; the value has as many elements less than itself as it has elements greater than itself.
median() finds the index of the median element.
The percentile() allows even more finely grained
slicing of the input data; for example, percentile($array, 95) finds the element at the 95th percentile. The
percentile() subroutine can be used to create
subroutines like quartile() and
decile().
We’ll use a worst-case linear algorithm, subroutine
selection(), for finding the
th element and build
median() and further functions on top of it. The
basic idea of the algorithm is first to find the median of
medians of small partitions (size 5) of the original array.
Then we either recurse to earlier elements, are happy with the median
we just found and return that, or recurse to later elements:
use constant PARTITION_SIZE => 5;
# NOTE 1: the $index in selection() is one-based, not zero-based as usual.
# NOTE 2: when $N is even, selection() returns the larger of
# "two medians", not their average as is customary--
# write a wrapper if this bothers you.sub selection {
# $array: an array reference from which the selection is made.
# $compare: a code reference for comparing elements,
# must return -1, 0, 1.
# $index: the wanted index in the array.
my ($array, $compare, $index) = @_;
my $N = @$array;
# Short circuit for partitions.
return (sort { $compare->($a, $b) } @$array)[ $index-1 ]
if $N <= PARTITION_SIZE;
my $medians;
# Find the median of the about $N/5 partitions.
for ( my $i = 0; $i < $N; $i += PARTITION_SIZE ) {
my $s = # The size of this partition.
$i + PARTITION_SIZE < $N ?
PARTITION_SIZE : $N - $i;
my @s = # This partition sorted.
sort { $array->[ $i + $a ] cmp $array->[ $i + $b ] }
0 .. $s-1;
push @{ $medians }, # Accumulate the medians.
$array->[ $i + $s[ int( $s / 2 ) ] ];
}
# Recurse to find the median of the medians.
my $median = selection( $medians, $compare, int( @$medians / 2 ) );
my @kind;
use constant LESS => 0;
use constant EQUAL => 1;
use constant GREATER => 2;
# Less-than elements end up in @{$kind[LESS]},
# equal-to elements end up in @{$kind[EQUAL]},
# greater-than elements end up in @{$kind[GREATER]}.
foreach my $elem (@$array) {
push @{ $kind[$compare->($elem, $median) + 1] }, $elem;
}
return selection( $kind[LESS], $compare, $index )
if $index <= @{ $kind[LESS] };
$index -= @{ $kind[LESS] };
return $median
if $index <= @{ $kind[EQUAL] };
$index -= @{ $kind[EQUAL] };
return selection( $kind[GREATER], $compare, $index );
}
sub median {
my $array = shift;
return selection( $array,
sub { $_[0] <=> $_[1] },
@$array / 2 + 1 );
}
sub percentile {
my ($array, $percentile) = @_;
return selection( $array,
sub { $_[0] <=> $_[1] },
(@$array * $percentile) / 100 );
}We can find the top decile of a range of test scores as follows:
@scores = qw(40 53 77 49 78 20 89 35 68 55 52 71); print percentile(\@scores, 90), "\n";
77
Beating O(N log N)
All the sort algorithms so far have been “comparison”
sorts—they compare keys with each other. It can be proven
that comparison sorts cannot be faster than
. However you try
to order the comparisons, swaps, and inserts, there will always be at
least of them. Otherwise,
you couldn’t collect enough information to perform the sort.
It is possible to do better.
Doing better requires knowledge about the keys
before the sort begins. For instance, if you
know the distribution of the keys, you can beat .
You can even beat knowing
only the length of the keys. That’s what the radix sort does.
Radix sorts
There are many radix
sorts. What they all have in common is that each uses the
internal structure of the keys to speed up the sort. The
radix is the unit
of structure; you can think it as the base of the number
system used. Radix sorts treat the keys as numbers (even
if they’re strings) and look at them digit by digit. For example, the
string ABCD can be seen as a number in base 256
as follows:
.
The keys have to have the same number of bits because radix algorithms
walk through them all one by one. If some keys were shorter than
others, the algorithms would have no way of knowing whether a key
really ended or it just had zeroes at the end. Variable length
strings therefore have to be padded with zeroes
(\x00) to equalize the lengths.
Here, we present the straight radix
sort, which is interesting because of its rather
counterintuitive logic: the keys are inspected starting from their
ends. We’ll use a radix of 
because it holds all 8-bit characters. We assume that all the keys
are of equal length and consider one character at a time. (To consider
characters at a time, the keys
would have to be zero-padded to a length evenly divisible by
). For each pass,
$from contains the results of the previous pass:
256 arrays, each containing all of the elements with that 8-bit
value in the inspected character position. For the first pass, $from contains
only the original array.
Radix sort is illustrated in Figure 4-10
and implemented in the radix_sort() subroutine
as follows:
sub radix_sort {
my $array = shift;
my $from = $array;
my $to;
# All lengths expected equal.
for ( my $i = length $array->[ 0 ] - 1; $i >= 0; $i-- ) {
# A new sorting bin.
$to = [ ];
foreach my $card ( @$from ) {
# Stability is essential, so we use push().
push @{ $to->[ ord( substr $card, $i ) ] }, $card;
}
# Concatenate the bins.
$from = [ map { @{ $_ || [ ] } } @$to ];
}
# Now copy the elements back into the original array.
@$array = @$from;
}
We walk through the characters of each key, starting with the last. On each iteration, the record is appended to the “bin” corresponding to the character being considered. This operation maintains the stability of the original order, which is critical for this sort. Because of the way the bins are allocated, ASCII ordering is unavoidable, as we can see from the misplaced wolf in this sample run:
@array = qw(flow loop pool Wolf root sort tour);radix_sort(\@array);print "@array\n";Wolf flow loop pool root sort tour
For you old-timers out there, yes, this is how card decks were sorted when computers were real computers and programmers were real programmers. The deck was passed through the machine several times, one round for each of the card columns in the field containing the sort key. Ah, the flapping of the cards...
Radix sort is fast: 
, where
is the length of the keys, in bits.
The price is the time spent padding the keys to equal length.
Counting sort
Counting sort works for (preferably not too sparse) integer data. It simply first establishes enough counters to span the range of integers and then counts the integers. Finally, it constructs the result array based on the counters.
sub counting_sort {
my ($array, $max) = @_; # All @$array elements must be 0..$max.
my @counter = (0) x ($max+1);
foreach my $elem ( @$array ) { $counter[ $elem ]++ }
return map { ( $_ ) x $count[ $_ ] } 0..$max;
}Hybrid sorts
Often it is worthwhile to combine sort algorithms, first using a sort that quickly and coarsely arranges the elements close to their final positions, like quicksort, radix sort, or mergesort. Then you can polish the result with a shell sort, bubble sort, or insertion sort—preferably the latter two because of their unparalleled speed for nearly sorted data. You’ll need to tune your switch point to the task at hand.
Bucket sort
Earlier we noted that inserting new books into a bookshelf resembles an insertion sort. However, if you’ve only just recently learned to read and suddenly have many books to insert into an empty bookcase, you need a bucket sort. With four shelves in your bookcase, a reasonable first approximation would be to pile the books by the authors’ last names: A-G, H-N, O-S, T-Z. Then you can lift the piles to the shelves, and polish the piles with a fast insertion sort.
Bucket sort is very hard to beat for uniformly distributed numerical
data. The records are first dropped into the right
bucket. Items near each other (after
sorting) belong to the same bucket. The
buckets are then sorted using some other sort; here we use an
insertion sort. If the buckets stay small, the
running time of insertion
sort doesn’t hurt. After this, the buckets are simply
concatenated. The keys must be uniformly distributed; otherwise, the
size of the buckets becomes unbalanced and the insertion sort slows
down. Our implementation is shown in the
bucket_sort() subroutine:
use constant BUCKET_SIZE => 10;
sub bucket_sort {
my ($array, $min, $max) = @_;
my $N = @$array or return;
my $range = $max - $min;
my $N_BUCKET = $N / BUCKET_SIZE;
my @bucket;
# Create the buckets.
for ( my $i = 0; $i < $N_BUCKET; $i++ ) {
$bucket[ $i ] = [ ];
}
# Fill the buckets.
for ( my $i = 0; $i < $N; $i++ ) {
my $bucket = $N_BUCKET * (($array->[ $i ] - $min)/$range);
push @{ $bucket[ $bucket ] }, $array->[ $i ];
}# Sort inside the buckets.
for ( my $i = 0; $i < $N_BUCKET; $i++ ) {
insertion_sort( $bucket[ $i ] );
}
# Concatenate the buckets.
@{ $array } = map { @{ $_ } } @bucket;
}If the numbers are uniformly distributed, the bucket sort is quite possibly the fastest way to sort numbers.
Quickbubblesort
To further demonstrate hybrid sorts, we’ll marry quicksort and bubble
sort to produce quickbubblesort, or
qbsort() for short. We partition until our
partitions are narrower than a predefined threshold width, and then we
bubble sort the entire array. The partitionMo3()
subroutine is the same as the partition() subroutine
we used earlier, except that the median-of-three code has been inserted
immediately after the input arguments are copied.
sub qbsort_quick;
sub partitionMo3;
sub qbsort {
qbsort_quick $_[0], 0, $#{ $_[0] }, defined $_[1] ? $_[1] : 10;
bubblesmart $_[0]; # Use the variant that's fast for almost sorted data.
}
# The first half of the quickbubblesort: quicksort.
# A completely normal quicksort (using median-of-three)
# except that only partitions larger than $width are sorted.
sub qbsort_quick {
my ( $array, $first, $last, $width ) = @_;
my @stack = ( $first, $last );
do {
if ( $last - $first > $width ) {
my ( $last_of_first, $first_of_last ) =
partitionMo3( $array, $first, $last );
if ( $first_of_last - $first > $last - $last_of_first ) {
push @stack, $first, $first_of_last;
$first = $last_of_first;
} else {
push @stack, $last_of_first, $last;
$last = $first_of_last;
}
} else { # Pop.
( $first, $last ) = splice @stack, -2, 2;
}
} while @stack;
}
sub partitionMo3 {
my ( $array, $first, $last ) = @_;
use integer;
my $middle = int(( $first + $last ) / 2);
# Shuffle the first, middle, and last so that the median
# is at the middle.
@$array[ $first, $middle ] = @$array[ $middle, $first ]
if ( $$array[ $first ] gt $$array[ $middle ] );
@$array[ $first, $last ] = @$array[ $last, $first ]
if ( $$array[ $first ] gt $$array[ $last ] );
@$array[ $middle, $last ] = @$array[ $last, $middle ]
if ( $$array[ $middle ] lt $$array[ $last ] );
my $i = $first;
my $j = $last - 1;
my $pivot = $$array[ $last ];
# Now do the partitioning around the median.
SCAN: {
do {
# $first <= $i <= $j <= $last - 1
# Point 1.
# Move $i as far as possible.
while ( $$array[ $i ] le $pivot ) {
$i++;
last SCAN if $j < $i;
}
# Move $j as far as possible.
while ( $$array[ $j ] ge $pivot ) {
$j--;
last SCAN if $j < $i;
}
# $i and $j did not cross over,
# swap a low and a high value.
@$array[ $j, $i ] = @$array[ $i, $j ];
} while ( --$j >= ++$i );
}
# $first - 1 <= $j <= $i <= $last
# Point 2.
# Swap the pivot with the first larger element
# (if there is one).
if( $i < $last ) {
@$array[ $last, $i ] = @$array[ $i, $last ];
++$i;
}
# Point 3.
return ( $i, $j ); # The new bounds exclude the middle.
}
The qbsort() default threshold width of 10 can be
changed with the optional second parameter. We will see in the final
summary (Figure 4-14) how well this hybrid
fares.
External Sorting
Sometimes it’s simply not possible to contain all your data in memory.
Maybe there’s not enough virtual (or real) memory, or maybe some of
the data has yet to arrive when the sort begins. Maybe the items
being sorted permit only sequential access, like tapes in a tape
drive. This makes all of the algorithms
described so far completely impractical: they assume random access
devices like disks and memories. When the cost of retrieving or
storing an element becomes, say, linearly dependent on its position,
all the algorithms we’ve studied so far become at the least
because swapping two
elements is no longer 
as we have
assumed, but 
.
We can solve these problems using a divide-and-conquer technique, and the easiest is mergesort. Mergesort is ideal because it reads its inputs sequentially, never looking back. The partial solutions (saved on disk or tape) can then be combined over several stages into the final result. Furthermore, the finished output is generated sequentially, and each datum can therefore be finalized as soon as the merge “pointer” has passed by.
The mergesort we described earlier in this chapter divided the sorting problem into two parts. But there’s nothing special about the number two: in our dividing and conquering, there’s no reason we can’t divide into three or more parts. In external sorting, this multiway-merging may be needed, so that instead of merging only two subsolutions, we can combine several simultaneously.
Sorting Algorithms Summary
Most of the time Perl’s own sort is enough because
it implements a fine-tuned quicksort in C. However, if you need a
customized sort algorithm, here are some guidelines for choosing one.
Reminder: In our graphs, both axes are scaled to 1.0 because the absolute numbers are irrelevant—that’s the beauty of O-analysis. The 1.0 of the running time axis is the slowest case: bubblesort for random data.
The data set used was a collection of randomly generated strings (except for our version of bucket sort, which understands only numbers). There were 100, 200,..., 1000 strings, with lengths varying from 20 to 100 characters (except for radix sort, which demands equal-length strings). For each algorithm, the tests were run with all three orderings: random, already ordered, and already reverse-ordered. To avoid statistical flutter (the computer used was a multitasking server), each test was run 10 times and the running times (CPU time, not real time) were averaged.
To illustrate the fact that the worst case behavior of the algorithm has very little to do with the computing power, comprehensive tests were run on four different computers, resulting in Figure 4-11. An insertion sort on random data was chosen for the benchmark because it curves quite nicely. The computers sported three different CPU families, the frequencies of the CPUs varied by a factor of 7, and the real memory sizes of the hosts varied by a factor of 64. Due to these large differences the absolute running times varied by a factor of 4, but since the worst case doesn’t change, the curves all look similar.
O(N2) Sorts
In this section, we’ll compare selection sort, bubble sort, and insertion sort.
Selection sort
Selection sort is insensitive, but to little gain: performance is
always 
. It always does the
maximum amount of work that one can actually do without repeating
effort. It is possible to code stably, but not worth the trouble.
Bubble sort and insertion sort
Don’t use bubble sort or insertion sort by themselves because of their
horrible average performance,
, but remember their
phenomenal nearly linear performance when the data is already nearly
sorted. Either is good for the second stage of a hybrid sort.
insertion_merge() can be used for merging two
sorted
collections.
In Figure 4-12, the three upward curving
lines are the 
algorithms,
showing you how the bubble, selection, and insertion sorts perform for
random data.
To avoid
cluttering the figure, we show only one log-linear curve and one linear
curve. We’ll zoom in to the speediest region soon.
The bubble sort is the worst, but as you can see, the
more records there are, the quicker the deterioration for all three.
The second lowest line is the archetypal algorithm:
mergesort. It looks like a straight
line, but actually curves slightly upwards (much more gently than
). The best-looking (lowest)
curve belongs to radix sort: for random data, it’s
linear with the number of records.
O(N log N) Sorts
Figure 4-13 zooms in on the bottom region of
Figure 4-12. In the
upper left, the 
algorithms
shoot up aggressively. At the diagonal and clustering below it, the
algorithms curve up in a
much more civilized manner. At the bottom right are the four
algorithms: from top to bottom, they are
radix, bucket sort for uniformly distributed numbers, and the bubble
and insertion sorts for nearly ordered records.
Mergesort
Always performs well (). The large space requirement
(as large as the
input) of traditional implementations is a definite minus. The algorithm
is inherently recursive, but can and should
be coded iteratively. Useful for external
sorting.
Quicksort
Almost always performs well——but is very sensitive in its basic form.
Its Achilles’ heel is ordered or reversed data, yielding
performance. Avoid
recursion and use the median-of-three technique to make the worst case
very unlikely. Then the behavior reverts to log-linear even for
ordered and reversed data. Unstable. If you want stability, choose
mergesort.
How Well Did We Do?
In Figure 4-14, we present
the fastest general-purpose algorithms (disqualifying radix, bucket,
and counting): the iterative mergesort, the iterative
quicksort, our iterative median-of-three-quickbubblesort, and Perl’s
sort, for both random and ordered data. The
iterative quicksort for ordered data is not shown because of its
aggressive quadratic behavior.
As you can see, we can approach Perl’s built-in
sort, which as we said before is a quicksort under
the hood.[21] You can see how creatively combining
algorithms gives us much higher and more balanced performance than
blindly using one single algorithm.
Here are two tables that summarize the behavior of the sorting algorithms described in this chapter. As mentioned at the very beginning of this chapter, Perl has implemented its own quicksort implementation since Version 5.004_05. It is a hybrid of quicksort-with-median-of-three (quick+mo3 in the tables that follow) and insertion sort. The terminally curious may browse pp_ctl.c in the Perl source code.
Table 4-1 summarizes the performance behavior of the algorithms as well as their stability and sensitivity.
|
Sort |
Random |
Ordered |
Reversed |
Stability |
Sensitivity |
|
selection |
stable |
insensitive | |||
|
bubble |
unstable |
sensitive | |||
|
insertion |
stable |
sensitive | |||
|
shell |
stable |
sensitive | |||
|
merge |
stable |
insensitive | |||
|
heap |
unstable |
insensitive | |||
|
quick |
unstable |
sensitive | |||
|
quick+mo3 |
unstable |
insensitive | |||
|
radix |
stable |
insensitive | |||
|
counting |
stable |
insensitive | |||
|
bucket |
stable |
sensitive |
The quick+mo3 is quicksort with the median-of-three enhancement. “Almost ordered” and “almost reversed” behave like their perfect counterparts...almost.
Table 4-2 summarizes the pros and cons of the algorithms.
J. R. R. Tolkien, The Lord of the Rings
“No, not at the rear!” the slave-driver shouted. “Three files up. And stay there, or you’ll know it, when I come down the line!”
[12] The (3)
is Unix-speak and means documentation section 3, the libraries.
On a Unix system, man qsort will display
the documentation.
[13] Actually, there is at least one port of Perl, to the IBM System/390, which uses another ordering, EBCDIC.
[14] The Royal Academy at Madrid recently gave in a bit, thanks to the stupidity of computers: handling the letter ch as c and h is now acceptable.
[15] You LISP hackers will recognize the trick.
[16] Strictly speaking, the “left” and “right” are misnomers: left means “the first elements of the anonymous lists” and right means “the second elements of the anonymous lists.”
[17] ISO Latin 1 is a character encoding like ASCII. In fact, ASCII and the first half of ISO Latin 1 are identical. The second half of ISO Latin 1 contains many of the accented characters of several Western European languages.
[18] 200-MHz Pentium Pro, 64 MB memory, NetBSD 1.2G.
[19] As in Rigoletto: La donna è mobile.
[20] Expert poker and bridge players don’t do this, however. They leave their cards unsorted because moving the cards around reveals information.
[21] The better qsort()
implementations actually are also hybrids, often quicksort combined
with insertion sort.
Get Mastering Algorithms with Perl now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
