Numeracy (the ability to use numbers) is as important as literacy. And while people vary in mathematical aptitude, almost everyone can improve their math skills, because numbers are happy to repay the effort of making their acquaintance.
Because so many people in our culture have trouble with math, improving your math skills will not only help you directly, but can also help you look good and give you an edge at work or school. In keeping with the "mental arts" approach outlined in the Preface, most of the hacks in this chapter involve mental math: math you can do in your head.
You don't need a calculator to do simple math! Learn a few tricks, and with a little practice, you'll be surprised how much arithmetic you can do in your head.
Most people need a calculator to do even simple arithmetic. There's nothing wrong with that, but if a calculator isn't available, it can become a problem. And even if you don't count the time to find the calculator, mental arithmetic can actually be faster than a calculator, too.
Entire books have been written on mental arithmetic, so we're not going to cover everything in this hack. This hack covers some typical techniques useful in their own right, and some of the other hacks in this chapter are also useful in doing mental mathematics. If you find this hack interesting and useful, you can check out one of the many books on the subject, some of which are listed at the end of this hack.
You should start at a level that's not frustrating for you. If you reach for a calculator to multiply 8 × 7, start by learning the multiplication tables. Use paper and pencil at first, and check your work.
Suppose you need to add the following numbers:
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 +
1 |
You could add 9 + 8 to get 17, and then add 7 to that to get 24, and so on. But it's much easier to rearrange the addition:
9 + 1 + 8 + 2 + 7 + 3 + 6 + 4 +
5 |
Each of the first pairs of numbers adds up to 10. So, we have the following easy addition:
10 + 10 + 10 + 10 +
5 |
which is 45.
In addition to rearranging to find 10s (or 20s), rearranging numbers so that they're in descending order tends to help. For instance, suppose you're adding the following numbers:
1100000 270000 3300000 + 30000 ________
It's probably easier to rearrange that as follows:
3300000 1100000 270000 + 30000 ________
It's easier because you don't need to keep track of as many nonzero digits while adding 3,300,000 and 1,100,000. Adding 270,000 and 30,000 will also help, so you're left with 4,400,000 + 300,000—an easy sum that totals to 4,700,000.1
When you learned to do paper-and-pencil multiplication in school, you probably learned to work from right to left, carrying as you went:
12 841 x 74 _____ 3364 5887 _____ 62234
Notice that you had to carry twice, once in multiplying the 4 in 74 by the 4 in 841, and once in multiplying the 7 by that 4. If you try to do this mentally, you'll have to keep track of multiple numbers between steps. For instance, when multiplying the 7 by the 8, you need to remember the 3,364 from the first multiplication, the 87 you've already figured out, and the carried 2.
Instead of working right to left, let's work left to right, just multiplying one of the six pairs of digits at a time. We're not doing this just to be different; rather, we want to limit the amount of information we need to keep track of.
Before we attempt our previous example, let's do a simpler problem. Multiplying a two-digit number by another two-digit number turns out to be particularly nice. Suppose we need to multiply 42 × 29. We multiply each pair of numbers (keeping track of the powers of 10), starting at the left, and keep a running total:
The individual calculations look like this:
40 x 20 = 800 |
40 x 9 = 360, and
800 + 360 = 1,160 |
2 x 20 = 40, and
1,160 + 40 = 1,200 |
2 x 9 = 18, and
1,200 + 18 = 1,218 |
Notice that we have to remember only one number between steps; this remains true even for larger problems. Of course, there's nothing wrong with writing down that number if paper and pencil are handy, and you'll probably find this method is still easier and less error prone that the usual method.
Tip
Because you need the number for only a short time, the mnemonics from Chapter 1 probably aren't necessary here.
Moving from higher numbers to lower ones tends to work better because it's easier to add a small number to a large one. As a bonus, if you need only an estimate, you can stop after doing the first few multiplications.
Now, back to our initial example. It contains pairs of digits:
The calculations look like this:
800 x 70 =
56,000 |
800 x 4 = 3,200, and
56,000 + 3,200 =
59,200 |
40 x 70 = 2,800, and
59,200 + 2,800 =
62,000 |
40 x 4 = 160, and
62,000 + 160 = 62,160 |
1 x 70 = 70, and
62,160 + 70 = 62,230 |
1 x 4 = 4, and 62,230 + 4 = 62,234 |
Of course, this is the same answer that we got before; doing a problem two ways is a good way to check it.2
Tip
"Calculate Mental Checksums" [Hack #38] and "Estimate Orders of Magnitude" [Hack #41] discuss other ways of checking your work.
Which addition problem would you rather do: 79 +
87 or 80 +
86? Probably the second; it's
easier because the 80, ending in 0, is a friendly number [Hack #36]. For addition,
numbers ending in 0 are friendly because adding the
corresponding place is trivial (adding 0 to a number doesn't change
it). Thus, we can mentally add the tens place (8 +
8 = 16)
and then just append the 6 for the ones place to get the answer,
166.3
The trick for more difficult addition problems is to change
the problem without changing the answer so that we have friendly
numbers. For instance, if we had 79 +
87, we'd notice that 79 is near
the friendly number 80. To turn 79 into 80, we have to add 1, so to
keep the answer the same, we need to subtract 1 somewhere. Let's
subtract 1 from the other number, 87, to get 86 and do 80 +
86 = 166,
as in the previous example.
Tip
Alternatively, you can add 80 +
87 = 167, and subtract the 1 from the
result.
The same principle works with
multiplication.4 Suppose I ask you to
compute 300 ×
70 in your head. Multiplying
3 ×
7 = 21
and then adding the three 0s, you easily get 21,000. Again, the 0s
at the end make the multiplication easy.
If we need to multiply 302×
69, we can think as
follows:
302 x 69 = (300 + 2) x (70 -
1) |
Now we can do the same cross-multiplication we did before, but with bigger chunks:
300 x 70 =
21,000 |
300 x -1 = -300 and
21,000 - 300 = 20,700 |
2 x 70 = 140 and
20,700 + 140 = 20,840 |
2 x -1 = -2 and
20,840 - 2 = 20,838 |
Numbers that end in 0 are the friendliest, but factors
of 100 [Hack #36] are
pretty friendly, too. For instance, if you think about the factors
of 100, you'll find that 25 is a friendly number, and 75 is at least
the friend of a friend. Then, the example we used earlier, 841 ×
74, looks like this:
841 x 74 = 841 x (75 - 1) = 841 x
75 - 841 |
Remember the minus 841, and let's do 841 x 75:
841 x 75 = 841 x 3 x 25
= 2523 x 25
= (2524 - 1) x 25
= 2524 x 25 - 25
= 2524 x 100 / 4 - 25
= 252400 / 4 - 25
= 63100 - 25
= 63075Finally, subtract the leftover 841, part by part:
63,075 - 800 =
62,275 |
62,275 - 40 =
62,235 |
62,235 - 1 =
62,234 |
which is a third confirmation of the result!
All of these tricks rely on basic properties of integers. For instance, the first multiplication example we gave was 841 × 74. We figured that out by using:
841 x 74 = (800 + 40 + 1) x (70 + 4)
= 800 x (70 + 4) + 40 x (70 + 4) + 1 x (70 + 4)
= 800 x 70 + 800 x 4 + 40 x 70 + 40 x 4 + 1 x 70 + 1 x 4The first line uses the definition of the decimal number system [Hack #40], and the remaining lines are repeated applications of the distributive property.
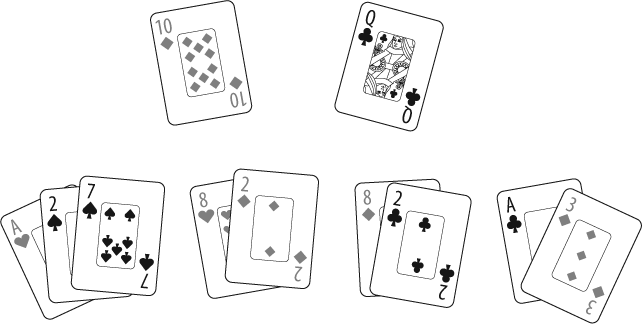
Suppose you're playing a card game [Hack #67] with a 52-card deck. Your final score is based on your final cards, and each number card is worth its number (so the 4 of hearts is worth 4 points), with an ace worth 1 point and each face card worth 10 points. Your hand is shown in Table 4-1.
The rearranging method works especially well because we have actual cards to rearrange.
Put the 10 and queen aside: they're worth 20 points. Then, arrange cards in the following groups (Figure 4-1):
Ace of hearts, 2 of spades, 7 of spades = 10 points
8 of hearts, 2 of diamonds = 10 points
8 of diamonds, 2 of clubs = 10 points
There are 50 points so far; we just need to add the remaining cards, which are the ace of clubs and the 3 of diamonds, for 4 more points. Your total score is 54 points, and you've probably figured this out so much faster than anyone else that you can double-check the rules to make sure the three 2s don't get you some kind of bonus.
Sticker, Henry. 1955. How to Calculate Rapidly. Dover.
Julius, Edward H. 1996. More Rapid Math: Tricks and Tips. Wiley.
Kelly, Gerard W. 1984. Short-Cut Math, Chapter 2. Dover.
Julius, Edward H. 1992. Rapid Math Tricks and Tips. Wiley.
Gardner, Martin. 1989. Mathematical Carnival. Mathematical Association of America. Chapters 6 and 7 discuss calculating prodigies and some of the tricks they used.
Doerfler, Ronald W. 1993. Dead Reckoning: Calculating Without Instruments. Gulf Publishing Company. This book is a bit more advanced. In addition to the basic operations, it covers extracting roots, and even higher mathematical functions, such as logarithms and trigonometric functions.
Mark Purtill
Get Mind Performance Hacks now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.