Modern Control System Theory and Design, 2nd Edition

8.4.  CONTROLLABILITY

The presentation of linear-state-variable feedback in Sections 8.2 and 8.3 assumed that all of the states are observable and measurable, and available to accept control signals (controllable). The concepts of controllability [2–4], and observability also play a very important role in optimal control theory (presented in the accompanying volume). Before designing a control system, we must determine whether it is controllable and its states are observable, since the conditions on controllability and observability often govern the existence of a solution to an optimal control system. Kalman [2,3] first introduced the concepts of controllability and observability in 1960. These concepts are basic in modern optimal control theory. This section develops mathematical tests to determine controllability, and the following section presents mathematical tests for determining observability.

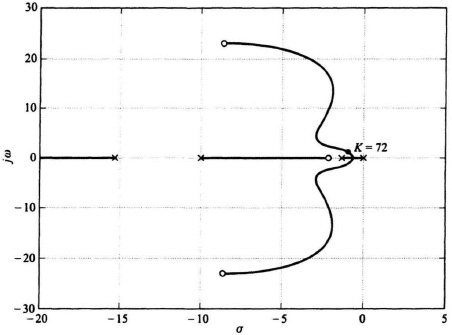
Figure 8.12  Root locus for the system of Figure 8.11 with the parameters of Eq. (8.51).

In order to introduce the concept of controllability, let us consider the simple open-loop system illustrated in Figure 8.13. A system is completely controllable if there exists a control which transfers every initial state at t = t₀ to any final state at t = T for all t₀ and T. Qualitatively, this means that the system G(s) is controllable if every state variable of G can be affected by the input ...