Solutions Manual to Accompany Game Theory: An Introduction, 2nd Edition

Matrix Two-Person Games

1.1   The Basics

Problems

1.1 There are 100 bankers lined up in each of 100 rows. Pick the richest banker in each row. Javier is the poorest of those. Pick the poorest banker in each column. Raoul is the richest of those. Who is richer: Javier or Raoul?

1.1 Answer: Think of this as a 100 × 100 game matrix and we are looking for the upper and lower values except that we are really doing it for the transpose of the matrix.

If we take the maximum in each row and then Javier is the minimum maximum, Javier is v⁺. If we take the minimum in each column, and Raoul is the maximum of those, then Raoul is the maximum minimum, or v⁻. Thus, Javier is richer.

Another way to think of this is that the poorest rich guy is wealthier than the richest poor guy. Common sense.

1.2 In a Nim game start with 4 pennies. Each player may take 1 or 2 pennies from the pile. Suppose player I moves first. The game ends when there are no pennies left and the player who took the last penny pays 1 to the other player.

(a) Draw the game as we did in 2 × 2 Nim.

1.2.a Answer: The game tree is

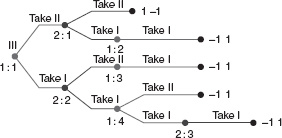
(b) Write down all the strategies for each player and then the game matrix.

1.2.b Answer:

Using the notation from the figure, we may list the strategies for player I as follows:

1. Go to 2 : 1; if at 1 : 2 ...