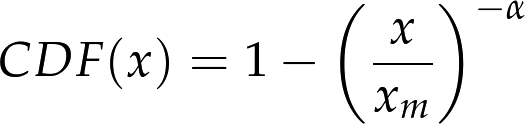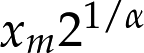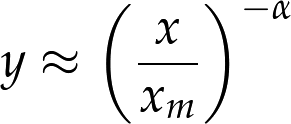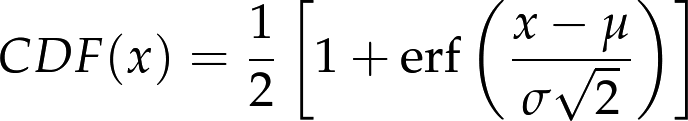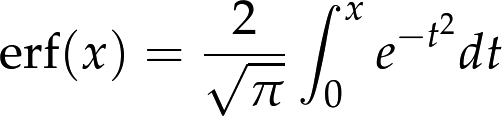The distributions we have used so far are called empirical distributions because they are based on empirical observations, which are necessarily finite samples.
The alternative is a continuous distribution, which is characterized by a CDF that is a continuous function (as opposed to a step function). Many real-world phenomena can be approximated by continuous distributions.
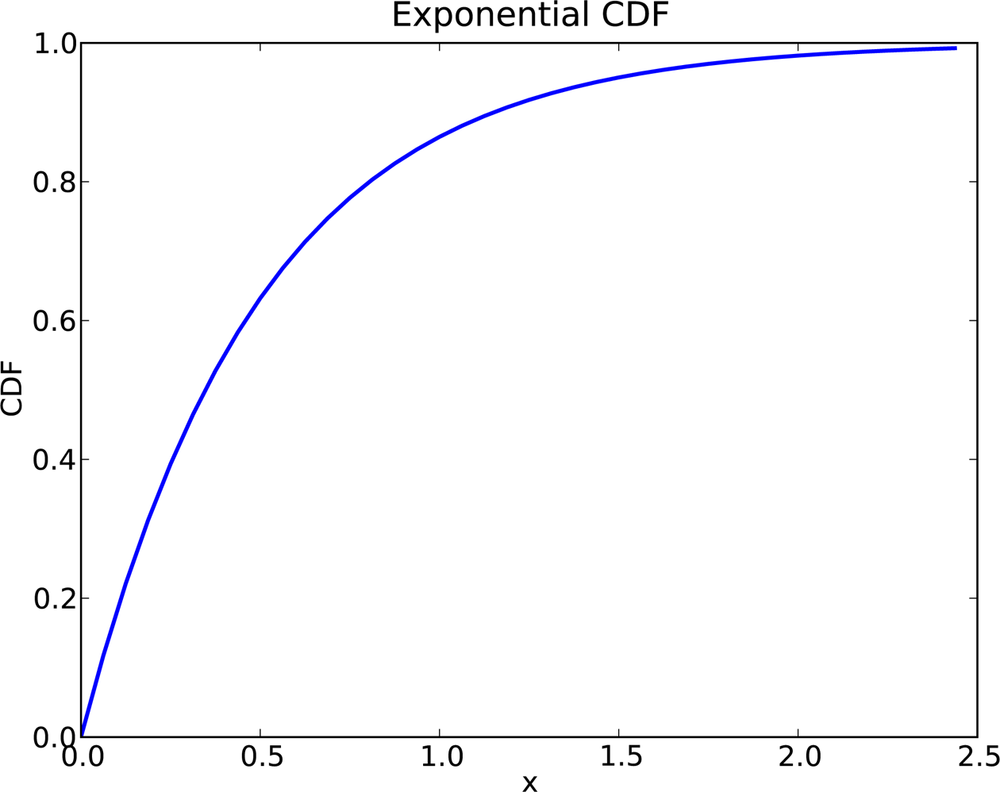
I’ll start with the exponential distribution because it is easy to work with. In the real world, exponential distributions come up when we look at a series of events and measure the times between events, which are called interarrival times. If the events are equally likely to occur at any time, the distribution of interarrival times tends to look like an exponential distribution.
The CDF of the exponential distribution is:
| CDF(x) = 1 - e -λx |
The parameter, λ, determines the shape of the distribution. Figure 4-1 shows what this CDF looks like with λ = 2.
In general, the mean of an exponential distribution is 1/λ, so the mean of this distribution is 0.5. The median is log(2)/λ, which is roughly 0.35.
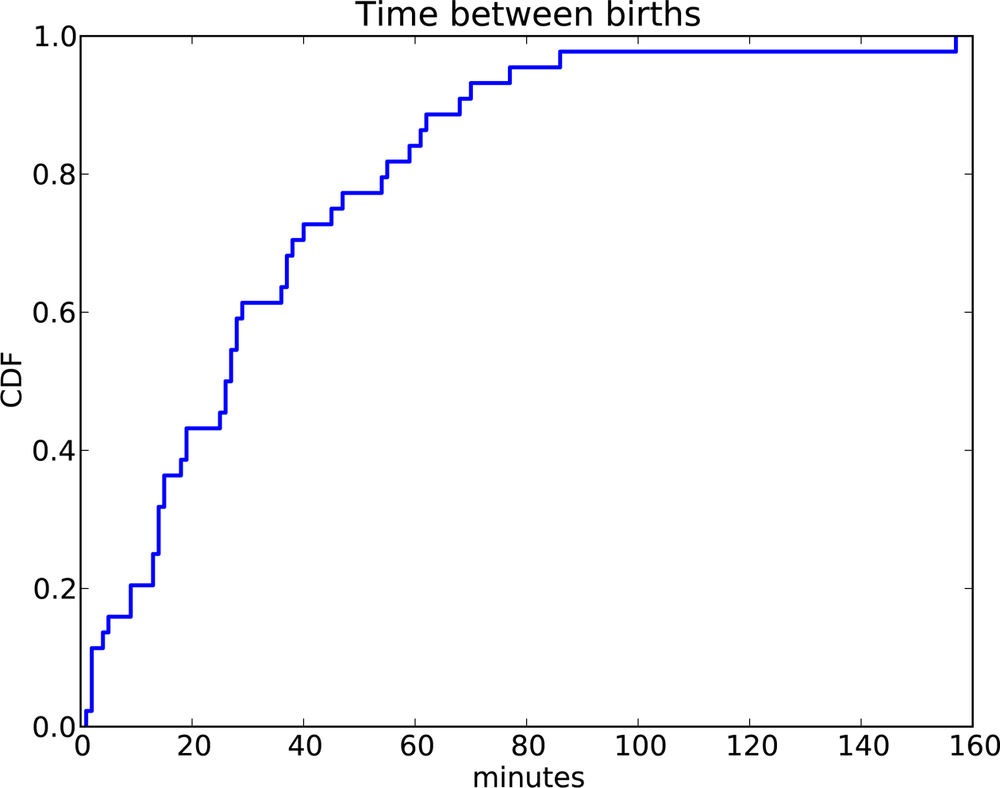
To see an example of a distribution that is approximately exponential, we will look at the interarrival time of babies. On December 18, 1997, 44 babies were born in a hospital in Brisbane, Australia.[7] The times of birth for all 44 babies were reported in the local paper; you can download the data from http://thinkstats.com/babyboom.dat.
Figure 4-2 shows the CDF of the interarrival times in minutes. It seems to have the general shape of an exponential distribution, but how can we tell?
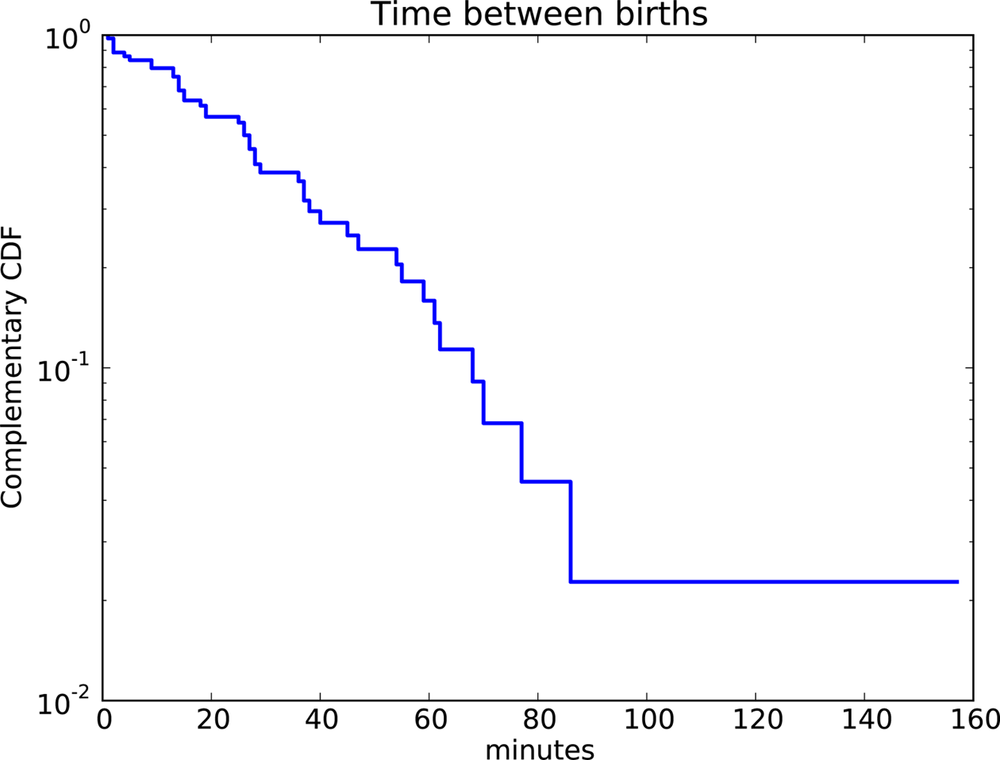
One way is to plot the complementary CDF, 1 − CDF(x), on a log-y scale. For data from an exponential distribution, the result is a straight line. Let’s see why that works.
If you plot the complementary CDF (CCDF) of a dataset that you think is exponential, you expect to see a function like:
| y ≈ e-λx |
Taking the log of both sides yields:
| log y ≈ -λx |
So on a log-y scale, the CCDF is a straight line with slope −λ.
Figure 4-3 shows the CCDF of the interarrivals on a log-y scale. It is not exactly straight, which suggests that the exponential distribution is only an approximation. Most likely the underlying assumption—that a birth is equally likely at any time of day—is not exactly true.
Example 4-1.
For small values of n, we don’t expect an empirical distribution to fit a continuous distribution exactly. One way to evaluate the quality of fit is to generate a sample from a continuous distribution and see how well it matches the data.
The function expovariate in
the random module generates random
values from an exponential
distribution with a given value of λ. Use it to
generate 44 values from an exponential distribution with mean 32.6.
Plot the CCDF on a log-y scale and compare
it to Figure 4-3.
Hint: You can use the function pyplot.yscale to plot the
y axis on a log scale.
Or, if you use myplot, the
Cdf function takes a boolean
option, complement, that determines
whether to plot the CDF or CCDF, and string options, xscale and yscale, that transform the axes; to plot a
CCDF on a log-y scale:
myplot.Cdf(cdf, complement=True, xscale='linear', yscale='log')
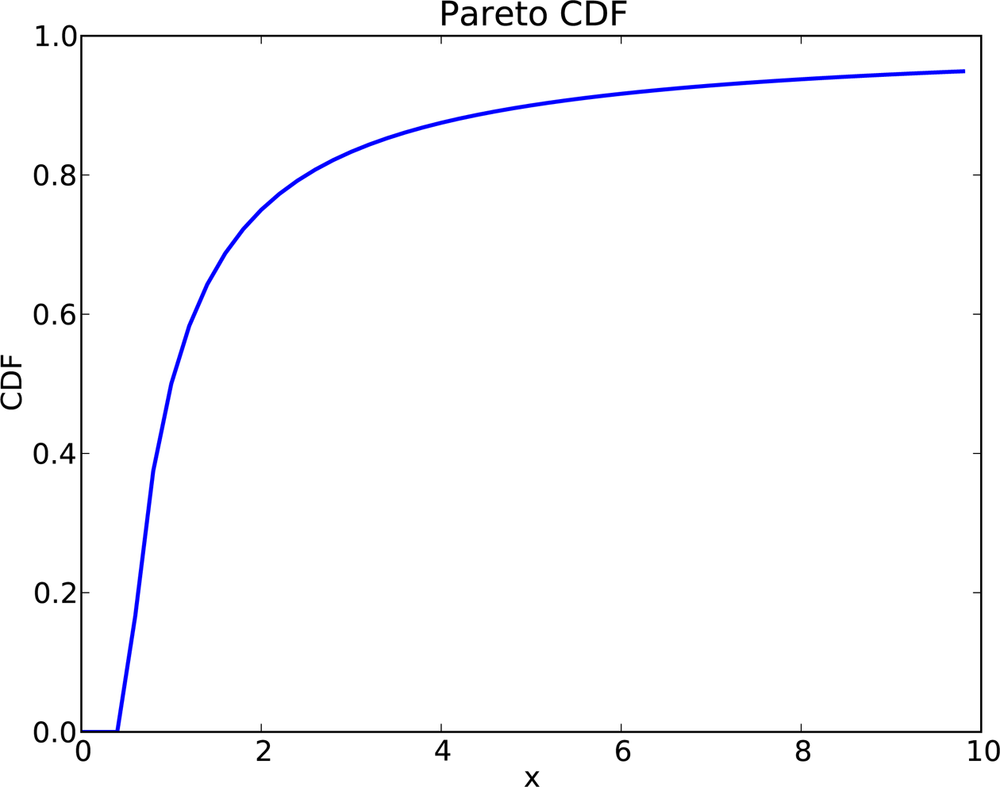
The Pareto distribution is named after the economist Vilfredo Pareto, who used it to describe the distribution of wealth (see http://wikipedia.org/wiki/Pareto_distribution). Since then, it has been used to describe phenomena in the natural and social sciences including sizes of cities and towns, sand particles and meteorites, forest fires and earthquakes.
The CDF of the Pareto distribution is:
The parameters xm and α determine the location and shape of the distribution. xm is the minimum possible value. Figure 4-4 shows the CDF of a Pareto distribution with parameters xm = 0.5 and α = 1.
The median of this distribution is:
which is 1, but the 95th percentile is 10. By contrast, the exponential distribution with median 1 has 95th percentile of only 1.5.
There is a simple visual test that indicates whether an empirical distribution fits a Pareto distribution: on a log-log scale, the CCDF looks like a straight line. If you plot the CCDF of a sample from a Pareto distribution on a linear scale, you expect to see a function like:
Taking the log of both sides yields:
| log y ≈ −α (log x − log xm) |
So if you plot log y versus log x, it should look like a straight line with slope −α and intercept α log xm.
Example 4-3.
The random module provides
paretovariate, which generates
random values from a Pareto distribution. It takes a parameter for
α, but not
xm.
The default value for
xm is
1; you can generate a distribution with a different parameter by
multiplying by
xm.
Write a wrapper function named paretovariate that takes
α and
xm as
parameters and uses random.paretovariate to generate values from
a two-parameter Pareto distribution.
Use your function to generate a sample from a Pareto distribution. Compute the CCDF and plot it on a log-log scale. Is it a straight line? What is the slope?
Example 4-4.
To get a feel for the Pareto distribution, imagine what the world would be like if the distribution of human height were Pareto. Choosing the parameters xm = 100 cm and α = 1.7, we get a distribution with a reasonable minimum, 100 cm, and median, 150 cm.
Generate 6 billion random values from this distribution. What is the mean of this sample? What fraction of the population is shorter than the mean? How tall is the tallest person in Pareto World?
Example 4-5.
Zipf’s law is an observation about how often different words are used. The most common words have very high frequencies, but there are many unusual words, like “hapaxlegomenon,” that appear only a few times. Zipf’s law predicts that in a body of text, called a “corpus,” the distribution of word frequencies is roughly Pareto.
Find a large corpus, in any language, in electronic format. Count how many times each word appears. Find the CCDF of the word counts and plot it on a log-log scale. Does Zipf’s law hold? What is the value of α, approximately?
Example 4-6.
The Weibull distribution is a generalization of the exponential distribution that comes up in failure analysis (see http://wikipedia.org/wiki/Weibull_distribution). Its CDF is:
Can you find a transformation that makes a Weibull distribution look like a straight line? What do the slope and intercept of the line indicate?
Use random.weibullvariate to
generate a sample from a Weibull distribution and use it to test your
transformation.
The normal distribution, also called Gaussian, is the most commonly used because it describes so many phenomena, at least approximately. It turns out that there is a good reason for its ubiquity, which we will get to in Central Limit Theorem.
The normal distribution has many properties that make it amenable for analysis, but the CDF is not one of them. Unlike the other distributions we have looked at, there is no closed-form expression for the normal CDF; the most common alternative is to write it in terms of the error function, which is a special function written erf(x):
The parameters μ and σ determine the mean and standard deviation of the distribution.
If these formulas make your eyes hurt, don’t worry; they are easy
to implement in Python.[8] There are many fast and accurate ways to approximate
erf(x). You can download one of them from http://thinkstats.com/erf.py, which provides functions
named erf and NormalCdf.
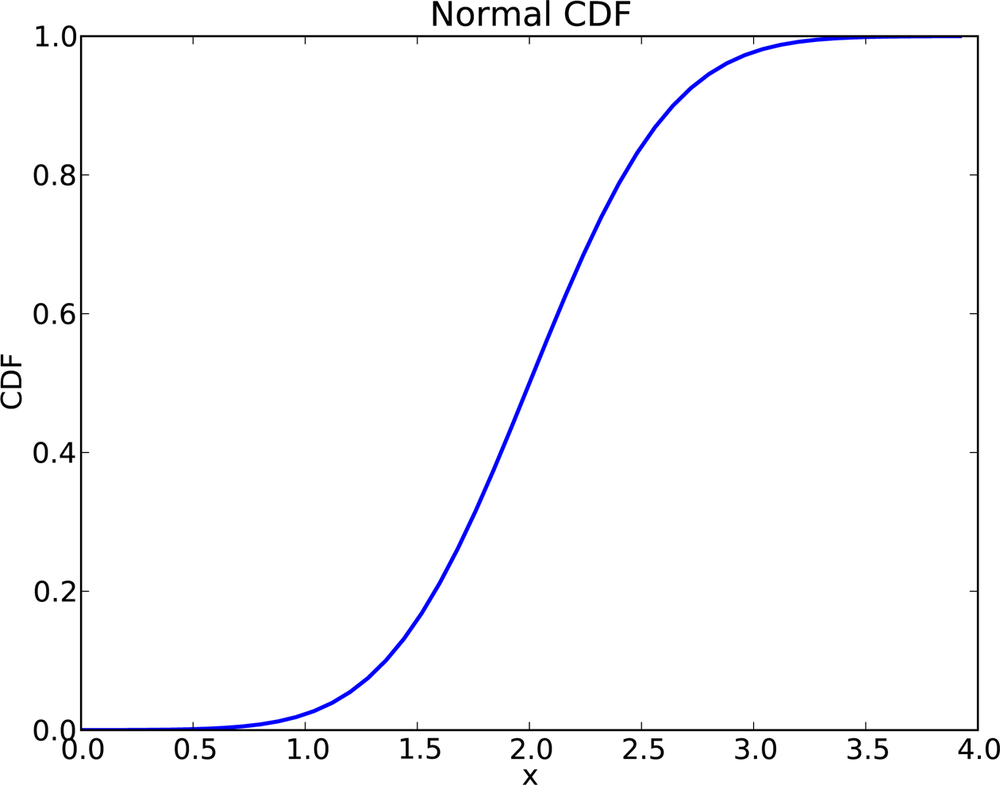
Figure 4-5 shows the CDF of the normal distribution with parameters μ = 2.0 and σ = 0.5. The sigmoid shape of this curve is a recognizable characteristic of a normal distribution.
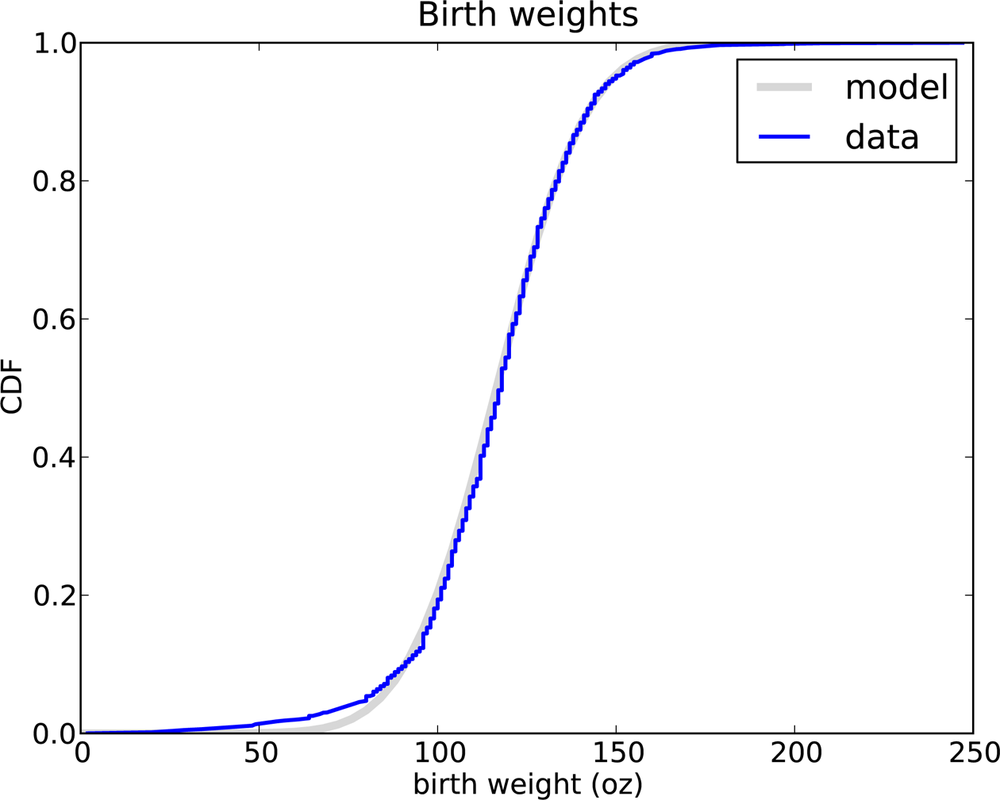
In the previous chapter, we looked at the distribution of birth weights in the NSFG. Figure 4-6 shows the empirical CDF of weights for all live births and the CDF of a normal distribution with the same mean and variance.
The normal distribution is a good model for this dataset. A model is a useful simplification. In this case it is useful because we can summarize the entire distribution with just two numbers, μ = 116.5 and σ = 19.9, and the resulting error (difference between the model and the data) is small.
Below the 10th percentile there is a discrepancy between the data and the model; there are more light babies than we would expect in a normal distribution. If we are interested in studying preterm babies, it would be important to get this part of the distribution right, so it might not be appropriate to use the normal model.
Example 4-7.
The Wechsler Adult Intelligence Scale is a test that is intended to measure intelligence.[9] Results are transformed so that the distribution of scores in the general population is normal with μ = 100 and σ = 15.
Use erf.NormalCdf to
investigate the frequency of rare events in a normal distribution.
What fraction of the population has an IQ greater than the mean? What
fraction is over 115? 130? 145?
A “six-sigma” event is a value that exceeds the mean by six standard deviations, so a six-sigma IQ is 190. In a world of six billion people, how many do we expect to have an IQ of 190 or more?[10]
Example 4-8.
Plot the CDF of pregnancy lengths for all live births. Does it look like a normal distribution?
Compute the mean and variance of the sample and plot the normal distribution with the same parameters. Is the normal distribution a good model for this data? If you had to summarize this distribution with two statistics, what statistics would you choose?
For the exponential, Pareto, and Weibull distributions, there are simple transformations we can use to test whether a continuous distribution is a good model of a dataset.
For the normal distribution, there is no such transformation, but there is an alternative called a normal probability plot. It is based on rankits: if you generate n values from a normal distribution and sort them, the kth rankit is the mean of the distribution for the kth value.
Example 4-9.
Write a function called Sample that generates six samples from a
normal distribution with μ = 0 and
σ = 1. Sort and return the
values.
Write a function called Samples that calls Sample 1,000 times and returns a list of
1,000 lists.
If you apply zip to this list
of lists, the result is six lists with 1,000 values in each. Compute
the mean of each of these lists and print the results. I predict that
you will get something like this:
{−1.2672, −0.6418, −0.2016, 0.2016, 0.6418, 1.2672}
If you increase the number of times you call Sample, the results should converge on these
values.
Computing rankits exactly is moderately difficult, but there are numerical methods for approximating them. And there is a quick-and-dirty method that is even easier to implement:
From a normal distribution with μ = 0 and σ = 1, generate a sample with the same size as your dataset and sort it.
Sort the values in the dataset.
Plot the sorted values from your dataset versus the random values.
For large datasets, this method works well. For smaller datasets, you can improve it by generating m(n+1) − 1 values from a normal distribution, where n is the size of the dataset and m is a multiplier. Then select every mth element, starting with the mth.
This method works with other distributions as well, as long as you know how to generate a random sample.
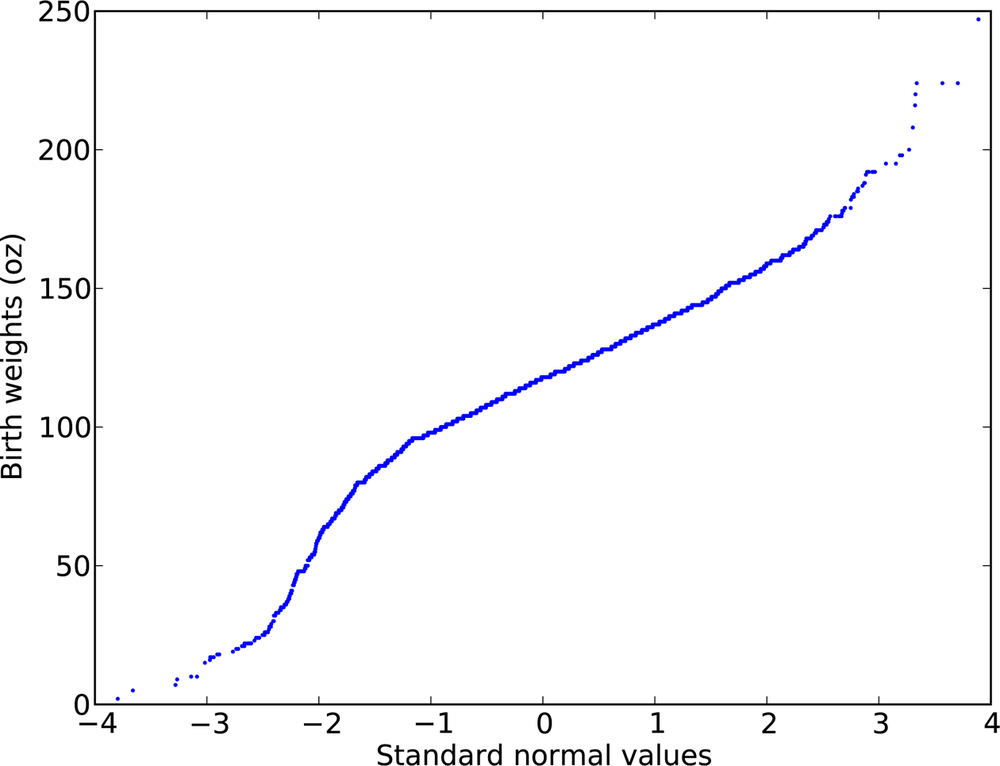
Figure 4-7 is a quick-and-dirty normal probability plot for the birth weight data.
The curvature in this plot suggests that there are deviations from a normal distribution; nevertheless, it is a good (enough) model for many purposes.
Example 4-10.
Write a function called NormalPlot that takes a sequence of values
and generates a normal probability plot. You can download a solution
from http://thinkstats.com/rankit.py.
Use the running speeds from relay.py to generate a normal probability
plot. Is the normal distribution a good model for this data? You can
download a solution from http://thinkstats.com/relay_normal.py.
If the logarithms of a set of values have a normal distribution, the values have a lognormal distribution. The CDF of the lognormal distribution is the same as the CDF of the normal distribution, with log x substituted for x.
| CDFlognormal(x) = CDFnormal(log x) |
The parameters of the lognormal distribution are usually denoted μ and σ. But remember that these parameters are not the mean and standard deviation; the mean of a lognormal distribution is exp(μ + σ2/2) and the standard deviation is ugly.[11]
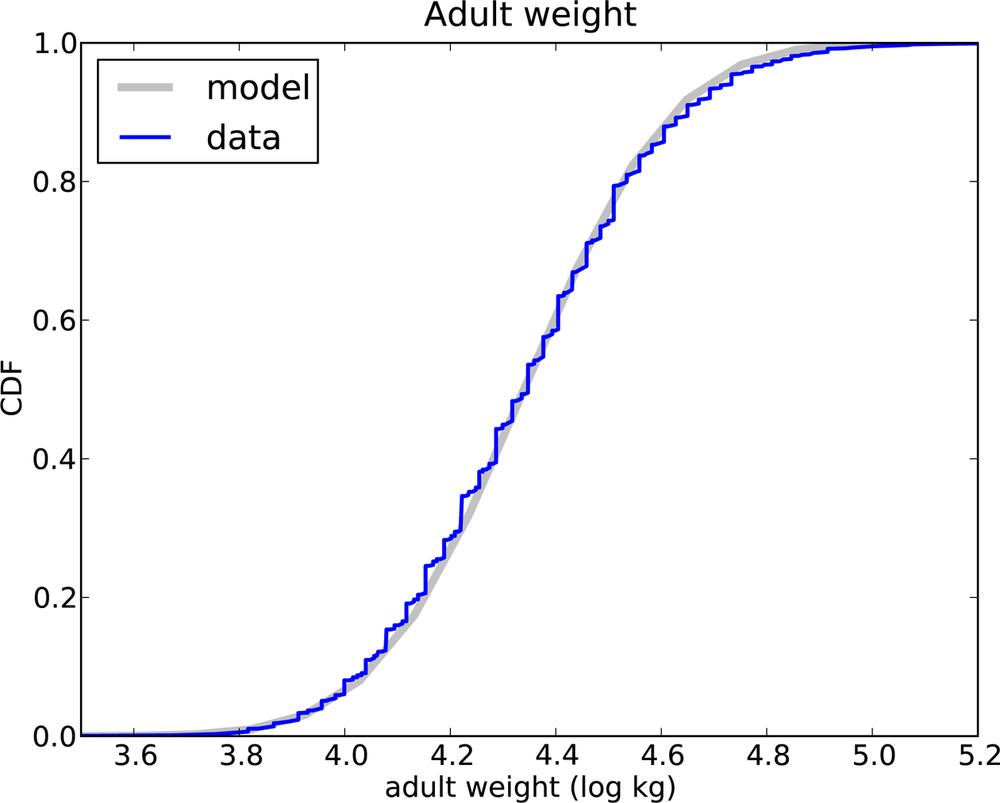
It turns out that the distribution of weights for adults is approximately lognormal.[12]
The National Center for Chronic Disease Prevention and Health Promotion conducts an annual survey as part of the Behavioral Risk Factor Surveillance System (BRFSS).[13] In 2008, they interviewed 414,509 respondents and asked about their demographics, health, and health risks.
Among the data they collected are the weights in kilograms of 398,484 respondents. Figure 4-8 shows the distribution of log w, where w is weight in kilograms, along with a normal model.
The normal model is a good fit for the data, although the highest weights exceed what we expect from the normal model even after the log transform. Since the distribution of log w fits a normal distribution, we conclude that w fits a lognormal distribution.
Example 4-11.
Download the BRFSS data from http://thinkstats.com/CDBRFS08.ASC.gz, and my code for
reading it from http://thinkstats.com/brfss.py.
Run brfss.py and confirm that it
prints summary statistics for a few of the variables.
Write a program that reads adult weights from the BRFSS and generates normal probability plots for w and log w. You can download a solution from http://thinkstats.com/brfss_figs.py.
Example 4-12.
The distribution of populations for cities and towns has been proposed as an example of a real-world phenomenon that can be described with a Pareto distribution.
The U.S. Census Bureau publishes data on the population of every incorporated city and town in the United States. I have written a small program that downloads this data and stores it in a file. You can download it from http://thinkstats.com/populations.py.
Read over the program to make sure you know what it does; then run it to download and process the data.
Write a program that computes and plots the distribution of populations for the 14,593 cities and towns in the dataset.
Plot the CDF on linear and log-x scales so you can get a sense of the shape of the distribution. Then plot the CCDF on a log-log scale to see if it has the characteristic shape of a Pareto distribution.
Try out the other transformations and plots in this chapter to see if there is a better model for this data.
What conclusion do you draw about the distribution of sizes for cities and towns? You can download a solution from http://thinkstats.com/populations_cdf.py.
Example 4-13.
The Internal Revenue Service of the United States (IRS) provides data about income taxes at http://irs.gov/taxstats.
One of their files, containing information about individual
incomes for 2008, is available from http://thinkstats.com/08in11si.csv. I converted it to a
text format called CSV, which stands for “comma-separated values”; you
can read it using the csv
module.
Extract the distribution of incomes from this dataset. Are any of the continuous distributions in this chapter a good model of the data? You can download a solution from http://thinkstats.com/irs.py.
At the beginning of this chapter, I said that many real-world phenomena can be modeled with continuous distributions. “So what?”, you might ask.
Like all models, continuous distributions are abstractions, which means they leave out details that are considered irrelevant. For example, an observed distribution might have measurement errors or quirks that are specific to the sample; continuous models smooth out these idiosyncrasies.
Continuous models are also a form of data compression. When a model fits a dataset well, a small set of parameters can summarize a large amount of data.
It is sometimes surprising when data from a natural phenomenon fit a continuous distribution, but these observations can lead to insight into physical systems. Sometimes we can explain why an observed distribution has a particular form. For example, Pareto distributions are often the result of generative processes with positive feedback (so-called preferential attachment processes: see http://wikipedia.org/wiki/Preferential_attachment.).
Continuous distributions lend themselves to mathematical analysis, as we will see in Chapter 6.
Continuous CDFs are also useful for generating random numbers. If there is an efficient way to compute the inverse CDF, ICDF(p), we can generate random values with the appropriate distribution by choosing from a uniform distribution from 0 to 1, then choosing:
| x = ICDF(p) |
For example, the CDF of the exponential distribution is:
| p = 1 − e-λx |
Solving for x yields:
| x = −log (1 − p) / λ |
So in Python we can write:
def expovariate(lam):
p = random.random()
x = -math.log(1-p) / lam
return xI called the parameter lam because lambda is a Python keyword. Most implementations
of random.random can return 0 but not
1, so 1 − p can be 1 but not 0,
which is good, because log 0 is undefined.
- continuous distribution
- corpus
- empirical distribution
- error function
A special mathematical function, so named because it comes up in the study of measurement errors.
- hapaxlegomenon
A word that appears only once in a corpus. It appears twice in this book, so far.
- interarrival time
- model
A useful simplification. Continuous distributions are often good models of more complex empirical distributions.
- normal probability plot
A plot of the sorted values in a sample versus the expected value for each if their distribution is normal.
- rankit
The expected value of an element in a sorted list of values from a normal distribution.
[7] This example is based on information and data from Dunn, “A Simple Dataset for Demonstrating Common Distributions,” Journal of Statistics Education v.7, n.3 (1999).
[8] As of Python 3.2, it is even easier; erf is in the math module.
[9] Whether it does or not is a fascinating controversy that I invite you to investigate at your leisure.
[10] On this topic, you might be interested to read http://wikipedia.org/wiki/Christopher_Langan.
[12] I was tipped off to this possibility by a comment (without citation) at http://mathworld.wolfram.com/LogNormalDistribution.html. Subsequently I found a paper that proposes the log transform and suggests a cause: Penman and Johnson, “The Changing Shape of the Body Mass Index Distribution Curve in the Population,” Preventing Chronic Disease, 2006 July; 3(3): A74. Online at http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1636707.
[13] Centers for Disease Control and Prevention (CDC). Behavioral Risk Factor Surveillance System Survey Data. Atlanta, Georgia: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, 2008.
Get Think Stats now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.