Chapter 4. Restriction Views
Updating restrictions
Leads to no contradictions
—
The bulk of the remainder of this book consists of an investigation into what’s involved in updating “through” the various relational operators (to use the conventional jargon). Thus, this chapter can be seen as the first in a series. In it, I propose to examine in detail the question of updating restriction views specifically (i.e., updating “through” a restriction operation). Note, however, that many of the issues to be raised in connection with that specific question will turn out to have more general significance; thus, this chapter is thus partly a continuation of Chapter 3, in a way. I’ll begin by taking a closer look at the motivating example from Chapter 1 (with apologies for the small amount of repetition that closer look will necessarily entail).
The Motivating Example Revisited
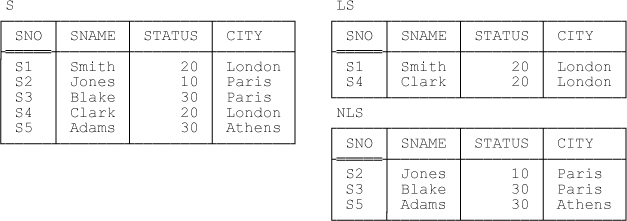
Just to remind you, the motivating example from Chapter 1 involved base relvar S (“suppliers”) from the suppliers-and-parts database and two restriction views of that base relvar, LS (“London suppliers”) and NLS (“non London suppliers”). Here are Tutorial D definitions:
VAR S BASE RELATION
{ SNO CHAR , SNAME CHAR , STATUS INTEGER , CITY CHAR }
KEY { SNO } ;
VAR LS VIRTUAL ( S WHERE CITY = 'London' )
KEY { SNO } ;
VAR NLS VIRTUAL ( S WHERE CITY ≠ 'London' )
KEY { SNO } ;Note: As we saw in the section Information Equivalence in Chapter 3, we could clearly arrange matters, at least conceptually, such that relvar S is the only relvar in some database DB1, relvars LS and NLS are the only relvars in another database DB2, and DB1 and DB2 are information equivalent. But first things first.
Now, as you can see from the definitions, {SNO} is a key (in fact, the sole key) for each of the three relvars; also, {SNO} is a foreign key in each of relvars LS and NLS, referencing the key {SNO} of relvar S, though I haven’t bothered to declare those foreign keys explicitly.[52] Note: As mentioned a couple of times in previous chapters, in practice we would probably drop attribute CITY from relvar LS, precisely because its value is constant (it’s always London); however, I won’t do that here, in order to keep the example simple. Of course, if we did drop that attribute, then LS would no longer be just a restriction as such of S anyway, and in this chapter I want to limit my attention to restriction specifically.
Sample values are shown in Figure 4-1.
Now let me remind you of The Principle of Interchangeability, which says there shouldn’t be any arbitrary and unnecessary distinctions between base relvars and views (i.e., views should “look and feel” just like base relvars so far as users are concerned). One consequence of that principle, in the case at hand, is that the behavior of relvars S, LS, and NLS shouldn’t depend on which of them are base relvars and which of them are views. Until further notice, therefore, let’s suppose they’re all base relvars:
VAR S BASE RELATION { ... } KEY { SNO } ;
VAR LS BASE RELATION { ... } KEY { SNO } ;
VAR NLS BASE RELATION { ... } KEY { SNO } ;Here repeated from Chapter 1 are the predicates for these three relvars (and note that here and elsewhere I favor the informal prose style for such predicates):
| S: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY. |
| LS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY is London). |
NLS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY isn’t London).[53]
As I also pointed out in Chapter 1, these relvars are subject to a number of constraints, over and above the key constraints already mentioned. (I didn’t state those constraints formally in Chapter 1, but now I will.) First of all, these two constraints obviously hold:[54]
CONSTRAINT ... LS = ( S WHERE CITY = 'London' ) ; CONSTRAINT ... NLS = ( S WHERE CITY ≠ 'London' ) ;
So do these two:
CONSTRAINT ... IS_EMPTY ( LS WHERE CITY ≠ 'London' ) ; CONSTRAINT ... IS_EMPTY ( NLS WHERE CITY = 'London' ) ;
The foregoing constraints imply certain additional ones (including certain foreign key constraints in particular, but again I won’t bother to show those):
CONSTRAINT ... S = UNION { LS , NLS } ;
CONSTRAINT ... DISJOINT { LS , NLS } ; Note: In connection with the first of these additional constraints, I should explain that Tutorial D—at least, the version of Tutorial D I’m using in this book—supports both dyadic (infix) and n-adic (prefix) versions of certain relational operators, including union in particular (also join, as we’ll see in the next chapter). Thus, for example, the union of LS and NLS can be expressed as either LS UNION NLS or (as above) UNION {LS,NLS}. In this book, I’ll use both styles—whichever suits my purpose best at the time. As for the second of those “additional” constraints, here I should explain that the Tutorial D expression DISJOINT {r1,…,rn} returns TRUE if and only if no two of the argument relations r1, …, rn have any tuples in common. Incidentally (as you might recall from Chapter 1), this particular constraint, along with the various key constraints, implies the following constraint as well:
CONSTRAINT ... DISJOINT { LS { SNO } , NLS { SNO } } ;(“no supplier number appears in both LS and NLS”).
Important: Observe how the foregoing constraints taken together ensure the information equivalence I mentioned earlier; in fact, they serve to show how each of the two designs, S by itself vs. the combination of LS and NLS, can be mapped into the other.
Aside: Of course, a database that contains all three relvars obviously involves some redundancy. Indeed, the foregoing constraints—at least, the multivariable ones—serve to capture those redundancies in a formal way. As I’ve explained elsewhere, however (see Database Design and Relational Theory), such redundancy shouldn’t cause any harm, just so long as it’s properly controlled. I’ll elaborate on this point briefly in the next section (More on Compensatory Actions). End of aside.
A note on terminology: Several of the foregoing CONSTRAINT statements—to be specific, all of the ones in which the boolean expression is of the form <relation expression> = <relation expression>—effectively require a certain equality dependency to hold (i.e., to be satisfied at all times). Here’s a definition:
Definition: An equality dependency (EQD for short) is a statement of the form rx1 = rx2, where the expressions rx1 and rx2 denote relations r1 and r2, respectively, and r1 and r2 are of the same type. The EQD is satisfied if and only if the bodies of r1 and r2 are equal.
Equality dependencies in turn are an important special case of a more general phenomenon known as inclusion dependencies:
Definition: An inclusion dependency (IND for short) is a statement of the form rx1 ⊆ rx2,where the expressions rx1 and rx2 denote relations r1 and r2, respectively, and r1 and r2 are of the same type. The IND is satisfied if and only if the body of r1 is a subset of the body of r2.
Points arising from this latter definition:
A foreign key constraint is a special case of an IND. In relvar LS, for example, {SNO} is a foreign key, referencing the key {SNO} in relvar S; thus, there’s an IND from LS to S—the projection of LS on SNO is included in the projection of S on SNO (in symbols, LS{SNO} ⊆ S{SNO}).
As already noted, an EQD is also a special case of an IND. In fact, the EQD r1 = r2 is equivalent to the pair of INDs r1 ⊆ r2 and r2 ⊆ r1; in other words, an EQD is an IND that “goes both ways,” as it were.
Although it’s not relevant to the topic of view updating as such, it would be remiss of me not to mention in passing that any constraint that can be expressed by means of a Tutorial D CONSTRAINT statement can in fact be expressed as an EQD (exercise for the reader!).
More on Compensatory Actions
In Chapter 1, we saw how certain compensatory actions could be used in connection with the motivating example to ensure that all of the applicable constraints continue to hold after updates are done. The compensatory actions (or rules) in question were as follows:
ON DELETEdFROM LS : DELETEdFROM S ; ON DELETEdFROM NLS : DELETEdFROM S ; ON DELETEdFROM S : DELETE (dWHERE CITY = 'London' ) FROM LS , DELETE (dWHERE CITY ≠ 'London' ) FROM NLS ; ON INSERTiINTO LS : INSERTiINTO S ; ON INSERTiINTO NLS : INSERTiINTO S ; ON INSERTiINTO S : INSERT (iWHERE CITY = 'London' ) INTO LS , INSERT (iWHERE CITY ≠ 'London' ) INTO NLS ;
These particular rules were explained in Chapter 1 (at least in outline), but there’s quite a lot more to be said about such rules in general; hence the present section. To be specific:
First of all, you might have already noticed that I’ve been a little sloppy in my use of terminology. To be specific, I’ve been using the term “compensatory action” to refer to both (a) the action, if any, that’s performed after some particular update operation has been done and (b) the formal specification of such an action in concrete syntax (though I’ve also used the term “rule” to refer to this latter construct). What’s more, I intend to continue this practice in the chapters ahead, and hope it won’t lead to confusion.
The rules in the example are expressed in a hypothetical and deliberately wordy extension to Tutorial D. Together, they serve to illustrate the kind of syntax I’ll be using for compensatory actions in the pages to come.[55] Note that d and i are effectively parameters to those rules, denoting the pertinent delete set and insert set after the update request for which the rule is compensating has been mapped to one of the form DELETE d FROM R, INSERT i INTO R. Note too, therefore, that d and i are disjoint.
It will often be the case that the compensatory actions can be stated in a variety of syntactically distinct but semantically equivalent forms. For example, the delete rule from S to LS and NLS—
ON DELETE
dFROM S : DELETE (dWHERE CITY = 'London' ) FROM LS , DELETE (dWHERE CITY ⊆ 'London' ) FROM NLS ;—could equally well be stated as follows:
ON DELETE
dFROM S : DELETE ( LS MATCHINGd) FROM LS , DELETE ( NLS MATCHINGd) FROM NLS ;It could even be stated as follows—
ON DELETE
dFROM S : DELETEdFROM LS , DELETEdFROM NLS ;—since an attempt to delete a tuple that doesn’t exist isn’t an error. As an extreme illustration of the point, it would always be possible to state the rules in terms of pure relational assignment alone.[56] Partly for pedagogic reasons, I prefer to state them in terms of explicit INSERTs and DELETEs instead. But I must emphasize that my primary concern in this book is always just to get the formulations logically correct; I’m not very interested at this stage in trying to find the simplest or most efficient formulations.
To elaborate on the previous point: I hope it’s obvious in general that, as noted in Chapter 2, my overall goal is always to get the theory right first and not to worry about implementation matters (not yet, at any rate). Doubtless there’ll be issues of optimization in any concrete implementation. Note: I’d like to mention one such issue here, however: Whenever the phrase DELETE d FROM R appears, that d can safely be replaced by d INTERSECT R; likewise, whenever the phrase INSERT i INTO R appears, that i can safely be replaced by i MINUS R. For simplicity, therefore, I’ll assume throughout what follows, without loss of generality, that these replacements have always been made, and hence that d MINUS R and i INTERSECT R are always both empty; in other words—previous remarks on this point notwithstanding—I’ll assume the rules as such never request insertion of a tuple that’s already present or deletion of one that isn’t.
Consider a user U who sees all three relvars S, LS, and NLS and performs (say) a DELETE on relvar S. Thanks to the delete rule on that relvar, then, that DELETE will cause tuples to be deleted from both relvar LS and relvar NLS (in general). That rule must therefore be explicitly visible to user U—for otherwise user U will perceive a violation of The Assignment Principle (again, in general). To be specific, if user U isn’t aware of that rule, then that user will at least potentially see a change to the dbvar—i.e., the variable that’s the entire database—that’s not exactly what he or she originally requested. Equivalently, that user will see changes to variables LS and/or NLS that he or she didn’t explicitly request at all. Hence, (a) compensatory actions can’t be wholly “under the covers” but must be exposed to users (at least in some cases), and (b) users must be explicitly aware that the updates they request are really shorthand for some extended series of operations—in fact, for a certain multiple assignment (again, at least in some cases).[57]
Following on from the previous point, an update explicitly requested by the user, together with any compensatory actions carried out in connection with that update, must be regarded in toto as a semantically atomic operation—a multiple assignment operation, to be precise. Thus, no integrity checking must be done until that multiple assignment has been executed in its entirety. Note: In general, as explained in Chapter 2, the individual assignments that make up a multiple assignment can be thought of as being executed simultaneously. In the case at hand, however, I’m going to assume for the purposes of this book, where it makes any difference, that the explicitly requested update is done first and the compensatory actions are done second (maybe AFTER would be a better keyword than ON). Please note, however, that this assumption is not logically required—it’s just that it has the effect of simplifying the formulation of the pertinent rules (usually).
A compensatory action, precisely because it is itself an update operation, might in general cause certain further compensatory actions to be performed, and so on. In the case of a DELETE on relvar S, for example, cascading the delete from S to LS will cause the cascade delete rule from LS to S to be invoked in turn. Of course, this second cascade won’t have any effect in this particular example; however, it does raise the interesting question of when cascading has to stop in general. I believe this issue deserves more study; for the purposes of this book, I’ll adopt the pragmatic position that it stops when a “fixpoint” is reached, meaning the database has reached a point when no further changes occur.[58] Note: If U1 is the update requested by the user, and the compensatory action for U1 causes another update request U2, which in turn causes another compensatory action to be performed (etc.), then U2 is “the explicitly requested update” as far as this latter compensatory action is concerned—and so on, recursively. Of course, the complete set of updates U1, U2, … must still behave as a semantically atomic operation.
Eventually I want to examine the case in which LS and NLS are views and S is a base relvar—but recall that, so far, all three relvars are base ones. Given that such is the case, I now observe that compensatory actions such as the ones we’ve been discussing are precisely what’s needed to control the redundancy among such relvars. In other words, I claim that compensatory actions would be needed anyway, in general, even if views as such weren’t supported at all. Note: Redundancy is said to be controlled if it does exist (and the user is aware of it), but the task of “propagating updates” to ensure that it never leads to any inconsistencies is managed by the system, not the user. (Uncontrolled redundancy can be a problem, but controlled redundancy shouldn’t be.) Controlling redundancy involves (a) explicitly declaring the redundancy to the DBMS and then (b) having the DBMS take responsibility for the necessary update propagation. And declaring the redundancy in the case at hand is, precisely, a matter of declaring the appropriate multivariable constraint(s).
The preceding point is actually a special case of a more general one, already touched on in Chapter 3: namely, that compensatory actions are needed anyway in order to maintain certain multivariable constraints. Of course, I’m assuming here that we don’t want users to be responsible for explicitly writing the necessary multiple assignment themselves whenever they do an update that might cause such a constraint to be violated. To put the point another way: By definition, multivariable constraints in general imply that certain updates must be, logically, multiple assignments. So we have a choice: Either (a) we require users always to write out those multiple assignments explicitly, or (b) we find a way of getting the system to do part of the work, such that users will often be able to get away with writing a single assignment instead. Compensatory actions are the means for achieving possibility (b).
One reviewer of an early draft of this book asked why, in the example of relvars S, LS, and NLS, the compensatory actions all had to be cascades. To be specific, he—the reviewer was male—pointed out (a) that SQL permits a “referential action” [sic] called NO ACTION that, instead of cascading, simply causes updates to fail if they would otherwise cause a referential integrity violation, and he therefore asked (b) why we couldn’t have a similar option in examples like the one under discussion. There are two responses to this question. First, specifying such an option would mean we would be requiring users always to write out those multiple assignments explicitly instead of getting the system to do part of the work (see the previous bullet item). Second, cascading will be what happens when we get to the real object of the exercise: namely, the situation in which (e.g.) S is a base relvar and LS and NLS are views.
There’s one final point I need to make in this section—but it’s an important one. It follows on from the previous point. Recall this text from the last section of Chapter 2 (Databases and Dbvars):
“Relation variables” (at least, relation variables in the database) aren’t really variables at all; rather, they’re a convenient fiction that gives the illusion that the database—or the dbvar, rather—can be updated piecemeal, individual relvar by individual relvar. And it … follows that “relational assignment,” multiple or otherwise, is also a convenient fiction, in a sense; to be specific, it’s an operator that lets us pretend that updating a dbvar can be thought of as a collection of updates on individual relvars within that dbvar.
What I need to say now, however, is this: These fictions aren’t always 100 percent sustainable. That is, in the context of updating in general, and view updating in particular, it isn’t always possible to use single assignment only (thereby updating the database individual relvar by individual relvar). Now, the compensatory actions to be described in detail in subsequent chapters do a pretty good job of maintaining those fictions, most of the time; but there are a few cases (which I’ll point out explicitly when we encounter them) where they can produce effects that might be unacceptable for some reason. And in such cases (cases, that is, where the effects aren’t fully acceptable), then I don’t think there’s any alternative to having the user write out an appropriate multiple assignment—which is to say, an appropriate database assignment, in effect—explicitly.
What About Triggers?
At this point I’d like to digress for a moment to head off at the pass, as it were, another objection that might have occurred to you—viz., isn’t this whole idea of compensatory actions just SQL-style triggers by another name? In other words, is there really anything new in what I’ve been saying?
Well, obviously there are some points of similarity between the two concepts; it might even be possible to use triggers to implement compensatory actions, if (as is typically the case today) the system provides little or no direct support for such actions.[59] But there are lots of differences too. Here are some of them:
Triggers can and often do involve procedural code. As a matter of fact, I checked several textbooks in this connection—textbooks both on commercial SQL products and on the SQL standard as such—and found the universal assumption to be that, in practice, triggers always do involve procedural code. By contrast, the compensatory actions I propose in this book are much more declarative in nature. (Of course, the terms declarative and procedural aren’t formally defined, so this point isn’t as precise as it might be. But what I mean by it is that the compensatory actions I propose are exactly as declarative as Tutorial D is in general. Moreover, the fact that they’re declarative in this sense means the DBMS can “understand” what those actions are meant to do and can reason about them in a formal way.)
Following on from the previous point, triggers in general can do anything at all—that is, they can involve procedures of arbitrary complexity—whereas all I want my compensatory actions to do is, at their most complex, some combination of relational INSERTs and DELETEs.
With triggers in general, there’s no notion that the system should be able to determine for itself what actions are to be performed (indeed, if it could, then triggers wouldn’t be necessary!). In other words, triggers are, by definition, user defined. With compensatory actions, by contrast, I’ve already said in Chapter 1 that the system should be able to work out for itself just what actions are required; in other words, such actions should be system defined, not user defined.
Details of the operation, and possibly even the existence, of triggers in general are typically concealed from the user. As a consequence, therefore, it’s highly likely from the user’s perspective that triggers will lead to violations of The Assignment Principle. Again, contrast the situation with compensatory actions.
In SQL in particular, triggers can and often do violate the set level nature of the relational model. As I said in Chapter 1, relational updates are set level by definition, and they mustn’t be treated as a sequence of individual tuple level updates (row level updates, in SQL); in particular, compensatory actions mustn’t be carried out until the update as requested by the user has been done in its entirety, and integrity constraints mustn’t be checked until that update and any associated compensatory actions have all been done in their entirety. Yet SQL supports what it calls row level triggers, which clearly violate these relational prescriptions.
Finally (again unlike triggers in general), the specific compensatory actions I propose in connection with view updating specifically are logically required,[60] thanks to The Principle of Interchangeability.
What About Explicit Update Operations?
Consider now the following explicit UPDATE operation on relvar S:
UPDATE S WHERE CITY = 'Paris' : { STATUS := 30 } ;As explained in SQL and Relational Theory, this operation is defined to be shorthand for the following relational assignment:
S := ( S WHERE CITY ≠ 'Paris' )
UNION
( EXTEND S WHERE CITY = 'Paris' : { STATUS := 30 } ) ;In other words, the overall effect of the update (conceptually, at least) is to delete the suppliers in Paris, and then reinsert those same suppliers, as it were, with their status set to 30. But observe now that these two sets—suppliers in Paris and suppliers in Paris with their status set to 30—might not be disjoint, because some suppliers in Paris might already have had status 30 before the update was done (supplier S3 is a case in point, given our usual sample values). Thus, if we want to ensure that the delete set d and the insert set i are indeed disjoint—which we do[61]—we must revise the expansion of the original UPDATE as indicated here:
S := ( S WHERE CITY ≠ 'Paris' OR STATUS = 30 )
UNION
( EXTEND S WHERE CITY = 'Paris' AND STATUS ≠ 30 ) :
{ STATUS := 30 } ) ;From this expansion we have d = suppliers in Paris with status something other than 30 and i = those same suppliers with status set to 30, and these two sets are disjoint as required.
Now, in the foregoing example I deliberately ignored the compensatory actions, since they were irrelevant to the point I wanted to make. But now let’s take a look at the effects of such actions in connection with explicit UPDATE operations specifically. Please keep in mind, however, that I’m still assuming that all relvars concerned are base relvars—no views yet. Note: The discussion that follows is partly (but only partly) a repeat of material from Chapter 1.
For a first example, consider the following UPDATE on relvar NLS:
UPDATE NLS WHERE SNO = 'S2' : { CITY := 'Oslo' } ;Let’s assume for simplicity that we know the city for supplier S2 isn’t Oslo already. Then what happens is this:
The existing tuple for supplier S2 is deleted from relvar NLS and a new tuple for that supplier, with CITY value Oslo, is inserted into that same relvar. .Note: I assume for simplicity here (and in examples throughout the book, wherever it’s helpful to do so) that we can talk in terms of deleting and inserting individual tuples as such, rather than relations. Technically, however, you should understand such talk as referring to sets of tuples, where the sets in question just happen to have cardinality one.
The existing tuple for supplier S2 is deleted from relvar S as well, thanks to the cascade delete rule from NLS to S, and the new tuple for that supplier, with CITY value Oslo, is inserted into relvar S as well, thanks to the cascade insert rule from NLS to S.
Note carefully that the foregoing DELETEs and INSERTs are all performed as part of the same atomic operation (a multiple assignment, of course); in particular, no integrity checking is done until all of those DELETEs and INSERTs have been done.
For a second example, consider this UPDATE on relvar S:
UPDATE S WHERE SNO = 'S2' : { CITY := 'London' } ;Let’s assume for simplicity that we know the city for supplier S2 isn’t already London. Then what happens is this:
The existing tuple for supplier S2 is deleted from relvar S and a new tuple for that supplier, with CITY value London, is inserted into that same relvar.
The existing tuple for supplier S2 is deleted from relvar NLS as well, thanks to the cascade delete rule from S to NLS, and the new tuple for that supplier, with CITY value London, is inserted into relvar LS as well, thanks to the cascade insert rule from S to LS. In other words, the tuple for supplier S2 has “migrated” from relvar NLS to relvar LS!—here speaking very loosely, of course.
For a final example, suppose the preceding UPDATE had been directed at relvar NLS rather than relvar S:
UPDATE NLS WHERE SNO = 'S2' : { CITY := 'London' } ;Now what happens is this:
The existing tuple for supplier S2 is deleted from relvar NLS.
An attempt is made to insert a new tuple for supplier S2, with CITY value London, into relvar NLS. That attempt fails, however, because it violates the constraint on relvar NLS that the CITY value in that relvar can never be London. So the update fails overall; the previous step (viz., deleting the original tple for supplier S2 from NLS) is undone, and the net effect is that the database remains unchanged.
Suppliers and Shipments
Note: This section is something of a digression and might well be skipped on a first reading. For one thing, the example it’s based on is different in kind from the one I’ve been considering in this chapter so far (i.e., London vs. non London suppliers)—it has to do with relvars S and SP from the suppliers-and-parts database, and of course there’s no question of one of those relvars being a restriction of the other, and certainly not of one being a view of the other. For another, the matters to be discussed, though they do have to do with updating in general, don’t seem to have much to do with view updating (or redundancy control) in particular. For such reasons, the discussion that follows doesn’t really belong in this chapter at all; rather, it ought to have been included in either Chapter 2 or Chapter 3. But it does rely on certain material—especially the material on explicit UPDATE operations from the section immediately preceding—that wasn’t covered (and couldn’t sensibly have been covered) in either Chapter 2 or Chapter 3; hence my decision to include it here.
Consider the foreign key constraint on the suppliers-and-parts database from the shipments relvar SP to the suppliers relvar S. Assume for the sake of discussion that we want to specify a cascade delete rule in connection with that foreign key, thus:[62]
ON DELETEdFROM S : DELETE ( SP MATCHINGd) FROM SP ;
Aside: Since relvar SP isn’t actually defined in terms of relvar S—in particular, SP isn’t a view of S—there’s no question of the DBMS determining, from the relvar definitions alone, just what rule(s) if any should apply in this situation. Rather, the DBA, or some suitably authorized user, will have to specify those rules explicitly, somehow. End of aside.
Now consider the following UPDATE operation on relvar S:
UPDATE S WHERE SNO = 'S1' : { STATUS := 10 } ;
Assume for simplicity that we know the status for supplier S1 isn’t already 10. What happens, then, is this:
The supplier tuple for supplier S1 is deleted from relvar S and a new tuple for that supplier, with STATUS value 10, is inserted into that same relvar.
The shipment tuples for supplier S1 are deleted from relvar SP as well, thanks to the cascade delete rule from S to SP. However, since there’s no cascade insert rule from S to SP, no shipment tuples are inserted into relvar SP corresponding to the new tuple in S for supplier S1. Net effect: The shipment tuples for supplier S1 are lost!
Note: It’s important to understand in this example that not only is there no cascade insert rule from S to SP, but there can’t be—because no such rule makes sense (right?).
But the foregoing state of affairs is surely unacceptable; I mean, we must surely be able to do things like changing the status of a supplier without losing all of that supplier’s shipments. Clearly, therefore, we need to do something about UPDATEs like the one in the example. But what?
The key to this problem, I think, lies in the recognition that, in general, updates involve both a delete set and an insert set, and hence that, in general, compensatory actions need to apply not just to delete or insert operations taken separately, but rather to such operations taken in combination. Here for example is an appropriate combined rule for the case of suppliers and shipments in particular (note the introduced names t1 and t2):
ON DELETEdFROM S , INSERTiINTO S : WITH (t1:= SP MATCHINGd,t2:= SP MATCHINGi) : DELETEt1FROM SP , INSERTt2INTO SP ;
Note: It would be tempting to formulate the compensatory actions without those introduced names, thus: DELETE (SP MATCHING d) FROM SP, INSERT (SP MATCHING i) INTO SP. The trouble with this formulation, however, is that, as explained in Appendix A, the symbol “SP” in the subexpression SP MATCHING i (in the INSERT portion of the formulation) denotes the value of relvar SP after the DELETE portion of the formulation has been applied.
By the way, let me point out in passing that no compensatory actions have been defined for relvar SP. Of course, this state of affairs doesn’t mean we can’t do updates on SP; it just means no compensatory actions will be performed if we do.
Now let’s revisit the UPDATE example discussed above (I repeat it here for convenience):
UPDATE S WHERE SNO = 'S1' : { STATUS := 10 } ;Given our usual sample values, we have the following (using a simplified notation for tuples once again, also for delete sets and insert sets):
d = the S tuple (S1,Smith,20,London)
i = the S tuple (S1,Smith,10,London)
t1 = existing SP tuples for supplier S1
t2 = existing SP tuples for supplier S1(same as t1)
As you can see, therefore, the net effect (loosely speaking) is to update the supplier tuple for S1, changing the status value from 20 to 10, while leaving relvar SP unchanged.
I’ll leave it as an exercise to confirm that explicit INSERT and DELETE operations on relvar S all continue to work as intuitively expected under the foregoing revised rule. But what about this UPDATE example?—
UPDATE S WHERE SNO = 'S1' : { SNO := 'S9' } ;Note that this is an example of what I referred to in Chapter 2 as a “key UPDATE” operation. This time we have:
d = the S tuple (S1,Smith,20,London)
i = the S tuple (S9,Smith,20,London)
t1 = existing SP tuples for supplier S1
t2 = empty
Thus, I think you can see that, even given our revised rule, tuples are still lost here; to be specific, the shipment tuples for supplier S1 simply “vanish”—they’re not replaced by tuples for supplier S9.
Now, examples like this one might be used, and indeed have been used (by myself among others, I hasten to add) to support arguments to the effect that what we really need is an explicit “cascade UPDATE rule” that, in the case under discussion, would cause an UPDATE on SNO in relvar S to cascade to update SNO in relvar SP (speaking very loosely, of course). But I’ve already given my reasons in Chapter 2 for rejecting such explicit UPDATE rules. To repeat what I said in that chapter, what we want is for compensatory actions to be driven by the applicable delete set and insert set, not by the arbitrary choice of syntax in which the pertinent update request happens to have been formulated. So I regard this approach as a nonstarter. Thus, it seems to me that if we want a change of key value in some tuple in relvar S to be replicated in corresponding tuples in relvar SP, then there’s no alternative to writing out the necessary multiple assignment explicitly (thereby, as noted earlier in the chapter, effectively writing out the necessary database assignment explicitly), like this:
UPDATE S WHERE SNO = 'S1' : { SNO := 'S9' } ,
UPDATE SP WHERE SNO = 'S1' : { SNO := 'S9' } ;Now what happens is this:
The supplier tuple for supplier S1 is deleted from relvar S and a new tuple, identical to its “old” counterpart except that the SNO value has been changed from S1 to S9, is inserted into that same relvar S. Likewise. all shipment tuples for supplier S1 are deleted from relvar SP and a set of new shipment tuples, identical to their “old” counterparts except that the SNO value has been changed from S1 to S9, is inserted into that same relvar SP.
The cascade delete rule from S to SP is invoked and requests deletion of all shipment tuples from relvar SP with SNO value S1. However, that request has no effect, since the pertinent tuples have already been deleted anyway by explicit user request. Net effect: The change of supplier number from S1 to S9 has been applied appropriately to both relvar S and relvar SP.
Note, therefore, that the cascade delete rule from S to SP serves no real purpose in this example. Of course, this fact doesn’t mean the rule is pointless—it’s still useful in connection with DELETE operations as such—but it doesn’t help with explicit UPDATE operations, as we’ve seen.
Anyway, the most important message from the discussion overall is this: In general, compensatory actions apply not just to delete or insert operations taken separately, but rather to such operations taken in combination. Of course, for any specific update, either the delete set d or the insert set i might be empty (and if d is empty, the rule reduces to a simple insert rule; if i is empty, it degenerates to a simple delete rule).
The Motivating Example Continued
Let’s get back to relvars S, LS, and NLS. Further, let’s continue to assume those relvars are all base relvars (still no views yet). However, let me now remind you that—conceptually speaking, at any rate—we can regard relvar S by itself as constituting a database DB1 and relvars LS and NLS together as constituting another database DB2, such that DB1 and DB2 are information equivalent. So let’s consider a user who sees just database DB2. That user:
Knows the corresponding predicates:
LS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY is London).
NLS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY isn’t London).
Is aware of all pertinent type information, is aware of the fact that {SNO} is a key for each of these relvars, and is aware of the following constraints:
CONSTRAINT ... IS_EMPTY ( LS WHERE CITY ≠ 'London' ) ; CONSTRAINT ... IS_EMPTY ( NLS WHERE CITY = 'London' ) ; CONSTRAINT ... DISJOINT { LS { SNO } , NLS { SNO } } ;Note that these constraints refer to relvars LS and NLS only (this user doesn’t even know relvar S exists).
Is not aware of any compensatory actions (because all of the compensatory actions in this example include some reference to relvar S).
And I hope you can see that, from this user’s perspective, all updates—all INSERTs, all DELETEs, all UPDATEs, and more generally all relational assignments—work exactly as expected.
Information Hiding
Now what about a user who sees only relvar NLS, say? Such a user knows the pertinent predicate (see above), knows the pertinent type information, knows also that {SNO} is a key for the relvar, and is aware of the following constraint:
CONSTRAINT ... IS_EMPTY ( NLS WHERE CITY = 'London' ) ;
Clearly, this user can’t be allowed to insert tuples into relvar NLS, nor to update supplier numbers within that relvar, because such operations have the potential to violate certain constraints that (of necessity) are hidden from the user in question. In other words, the user is seeing only part of the picture, as it were. As I put it in Chapter 1, there’s no magic! To state the matter a little more precisely, there’s no information equivalence here—there are clearly propositions that can be represented by relvar S and not by relvar NLS, and so it’s only to be expected that there’ll be operations available on relvar S that have no counterpart on relvar NLS when considered in isolation.
That said, I do need to elaborate somewhat … First of all, when I say some user “can’t be allowed” to perform some operation on some relvar, what I mean, of course, is that the user in question shouldn’t be granted the relevant authority. In other words, I’m assuming the DBA, or some other suitably authorized user, will use the authorization subsystem appropriately in order to ensure that operations that don’t make much sense can’t be attempted.
Second, to repeat something I said in Chapter 1, I suppose it might be possible to allow the user to perform such operations after all, just so long as he or she is prepared to accept occasional error messages to the effect that an operation is rejected simply “because the system says so,” without further explanation. The point is this: Whether such an operation succeeds or fails will depend in general, not only on those hidden constraints as such, but also on the current state of the hidden part of the database. (As a concrete illustration of this point, given our usual sample values, inserting the tuple (S1,Smith,20,Paris) into NLS will fail, while inserting (S6,Smith,20,Paris) will succeed.) From the user’s point of view, in other words, the behavior of such operations will be both unpredictable and (when they fail) inexplicable. Such a situation seems to me highly unattractive, and I therefore don’t propose that such a possibility be supported.
Third, I’ve said in effect that this user is allowed to update (say) supplier status values in relvar NLS but not to insert tuples into that relvar. Now, you might be wondering how this state of affairs can make sense—doesn’t it involve some kind of contradiction, given that we want to regard an UPDATE operation as shorthand for a certain DELETE / INSERT combination? But this latter fact is precisely the point: The implicit INSERT that’s performed as part of a (successful) explicit UPDATE is always accompanied by an implicit DELETE that guarantees that the INSERT in question doesn’t violate any constraints (including in particular ones that are hidden from this user). Thus, the fact that the user is allowed to perform certain explicit UPDATE operations certainly doesn’t imply that he or she has carte blanche to perform explicit INSERT operations as well.
Note: Remarks similar to those in the foregoing three paragraphs apply at numerous points in the pages ahead—essentially wherever I refer to some user as “not being allowed” to perform some operation—and I won’t bother to repeat them every time, instead letting those paragraphs do duty for all.
Putting it All Together
This section brings together for purposes of reference all of the relvar definitions, CONSTRAINT statements, and compensatory actions for the motivating example. However, given my argument in the previous chapter that it was a mistake to make a syntactic distinction between view and base relvar definitions, I’ll simplify the relvar definitions, just this once, in such a way as to elide that distinction:
VAR S ..... RELATION { ... } KEY { SNO } ;
VAR LS .... RELATION { ... } KEY { SNO } ;
VAR NLS ... RELATION { ... } KEY { SNO } ;
CONSTRAINT ... LS = ( S WHERE CITY = 'London' ) ;
CONSTRAINT ... NLS = ( S WHERE CITY ≠ 'London' ) ;
CONSTRAINT ... IS_EMPTY ( LS WHERE CITY ≠ 'London' ) ;
CONSTRAINT ... IS_EMPTY ( NLS WHERE CITY = 'London' ) ;
CONSTRAINT ... S = UNION { LS , NLS } ;
CONSTRAINT ... DISJOINT { LS { SNO } , NLS { SNO } } ;
ON DELETE d FROM S , INSERT i INTO S :
DELETE ( d WHERE CITY = 'London' ) FROM LS ,
DELETE ( d WHERE CITY ≠ 'London' ) FROM NLS ,
INSERT ( i WHERE CITY = 'London' ) INTO LS ,
INSERT ( i WHERE CITY ≠ 'London' ) INTO NLS ;
ON DELETE d FROM LS , INSERT i INTO LS :
DELETE d FROM S , INSERT i INTO S ;
ON DELETE d FROM NLS , INSERT i INTO NLS :
DELETE d FROM S , INSERT i INTO S ;As a matter of fact, we might consider combining the rules for the various compensatory actions still further. For example, the last two might be combined thus:
ON DELETEd1FROM LS , INSERTi1INTO LS , DELETEd2FROM NLS , INSERTi2INTO NLS : DELETEd1FROM S , DELETEd2FROM S , INSERTi1INTO S , INSERTi2INTO S ;
After all, multiple assignment means, loosely, that we can combine several distinct updates into a logically atomic operation, so why not do the same kind of thing with compensatory actions? In fact, it would theoretically be possible, though probably unattractive from a human factors point of view, to talk in terms of a single combined rule for the entire database. Then—thanks to Hugh Darwen for this observation—we’d have just one variable (the entire database), one rule (the combination of all compensatory actions), and one constraint (the total database constraint).
The Point at Last
Finally I come to my main point: Everything I’ve said in the chapter so far applies pretty much unchanged if some or all of the relvars concerned are views. For example, suppose as we originally did that S is a base relvar and LS and NLS are views. Then:
The constraints specified by the six CONSTRAINT statements in the previous section are enforced automatically, precisely because LS and NLS are views of S. That is, no update to any of the relvars can possibly cause any of those constraints to be violated.
The compensatory actions from S to LS and NLS also happen automatically, again because LS and NLS are views of S. That is, updates to S will automatically be reflected appropriately in LS or NLS or both. So the compensatory actions from S to LS and NLS are, in effect, derived: They’re derived from the corresponding view definitions[63] (where by “view definitions” I really mean the definitions of the mappings from the underlying base relvar(s) to the views in question—in other words, the pertinent “view defining expressions”).
Note: Observe in particular that, e.g., changing the supplier number for some supplier in S, say from S1 to S9, will cascade to either LS or NLS, whichever is applicable. By contrast, recall from the section Suppliers and Shipments that such a cascade won’t happen with S and SP. But that’s because the situation with S and SP is different: With S, LS, and NLS, we’re talking about what from the user’s point of view is just an example of controlled redundancy; with S and SP, such is not the case. (In fact, to pursue the point a moment longer, the whole point about the view updating scheme I’m proposing is to make the situation look to the user as if it were just a matter of controlled redundancy—assuming, that is, that the user in question sees both the views as such and the relvars in terms of which those views are defined. More particularly, telling the user about the compensatory actions means we don’t have to tell the user which relvars if any are base ones and which ones if any are views.)
The compensatory actions from LS and NLS to S—these are the ones that are generally thought of as the view updating rules as such—also happen automatically, again precisely because LS and NLS are views of S. That is, updates to LS or NLS are “really” updates to the underlying relvar S, and so are automatically visible in S, as well as in LS or NLS or both.
Now consider a user who sees only views LS and NLS. Then I hope you can see that the user in question can behave in all respects exactly as if those views were base relvars—in fact, exactly as described in the case where they actually were base relvars, in the section The Motivating Example Continued, earlier in this chapter. Which is, of course, the object of the exercise.
Note in particular that, e.g., an attempt to change the supplier city for some supplier in LS won’t cause the tuple in question to “migrate” from LS to NLS-instead, it will fail on a violation of The Golden Rule. By contrast, such migration would probably have been expected, and would probably have occurred, given traditional ad hoc approaches to view updating.[64]
By contrast, a user who sees, say, only view NLS will clearly be limited in the operations he or she is allowed to perform—again just like a user who sees only base relvar NLS, when all three relvars are base ones (again, see the section The Motivating Example Continued). Such a user will be allowed to delete tuples, and/or to update attributes other than attribute SNO, within relvar NLS, but that’s all. Once again, there’s no magic.
Note: In connection with this last point, it might be thought that the fact that a user who sees only view NLS is limited in the operations he or she is allowed to perform on that relvar constitutes a violation of The Principle of Interchangeability—but of course it doesn’t; as we’ve seen, the very same limitations apply in the case where NLS is a base relvar.
Overlapping Restrictions
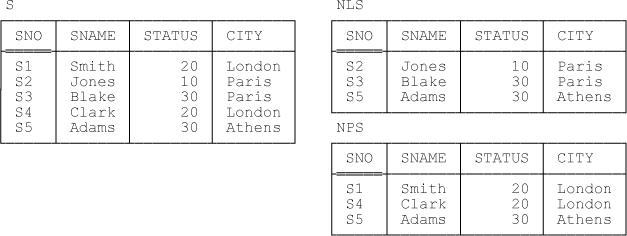
Let’s take a look at a slightly more complicated restriction example. Suppose we define two restriction views of the suppliers relvar S, NLS (“non London suppliers”) and NPS (“non Paris suppliers”). Both of these views have key {SNO}. Sample values are shown in Figure 4-2. Here are the predicates for the views:
| NLS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY isn’t London). |
| NPS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY isn’t Paris). |
The following constraints (actually EQDs) clearly hold:[65]
CONSTRAINT ... NLS = ( S WHERE CITY ≠ 'London' ) ; CONSTRAINT ... NPS = ( S WHERE CITY ≠ 'Paris' ) ;
So does this one (another EQD):
CONSTRAINT ... ( NLS WHERE CITY ≠ 'Paris' ) =
( NPS WHERE CITY ≠ 'London' ) ;As this latter constraint indicates, views NLS and NPS overlap, in the sense that, in general, certain tuples appear in both; in fact, the tuples in question must appear in both, in order to guarantee that the constraint is always satisfied. To spell the point out, a given tuple t appearing in relvar S will and must also appear in both NLS and NPS, if and only if the CITY value in that tuple t is neither London nor Paris. (I note in passing, therefore, that relvars NLS and NPS together violate The Principle of Orthogonal Design. See Database Design and Relational Theory for further explanation of this point.)
It follows that certain updates on either of NLS and NPS will necessarily cascade to the other one, albeit indirectly. For example, here are the insert rules for S, NLS, and NPS:[66]
ON INSERTiINTO S : INSERT (iWHERE CITY ≠ 'London' ) INTO NLS , INSERT (iWHERE CITY ≠ 'Paris' ) INTO NPS ; ON INSERTiINTO NLS : INSERTiINTO S ; ON INSERTiINTO NPS : INSERTiINTO S ;
Now observe what happens if we insert, say, the tuple (S6,Lopez,30,Madrid) into NLS. First of all, the insert cascades from NLS to S and the same tuple is thus inserted into relvar S; then this latter insert cascades from S to NPS, and the same tuple is inserted into this latter relvar as well. In effect, therefore, the insert has cascaded from NLS to NPS.
Here now are the delete rules (and observe that here too there’s potential for an operation on one of NLS and NPS to cascade to the other, indirectly):
ON DELETEdFROM S : DELETE (dWHERE CITY ≠ 'London' ) FROM NLS , DELETE (dWHERE CITY ≠ 'Paris' ) FROM NPS ; ON DELETEdFROM NLS : DELETEdFROM S ; ON DELETEdFROM NPS : DELETEdFROM S ;
So a user who sees just NLS and NPS and not S will sometimes observe cascades from one to the other. But of course we want that user to be able to think of NLS and NPS as base relvars. In other words, even if they really were base relvars, the existence of certain constraints implies that certain cascades logically ought to occur, even between base relvars, on occasion. Indeed, relvars NLS and NPS are subject to a certain redundancy, and I’ve already said that redundancy, when it exists, ought to be controlled—and that’s exactly what the cascade updates are doing (viz., propagating updates in order to control the redundancy). Here are the pertinent rules:
ON INSERTiINTO NLS : INSERT (iWHERE CITY ≠ 'Paris' ) INTO NPS ; ON INSERTiINTO NPS : INSERT (iWHERE CITY ≠ 'London' ) INTO NLS; ON DELETEdFROM NLS : DELETE (dWHERE CITY ≠ 'Paris' ) FROM NPS ; ON DELETEdFROM NPS : DELETE (dWHERE CITY ≠ 'London' ) FROM NLS ;
These rules are derived by combining the ones already given for S, NLS, and NPS and replacing references to S by references to NLS and/or NPS, as appropriate.
And what about information hiding?—for example, the case of a user who sees (say) just view NLS? I’ll leave detailed consideration of this possibility as an exercise.
Concluding Remarks
I have a few more points to make. The first is a small matter of terminology. I’ve been talking about “restriction views” and “updating through restrictions” I’ve said, for example, that view LS is a restriction of base relvar S. But restriction is an operation of the relational algebra; by definition, therefore, it doesn’t really apply to relvars, it applies to relations. So what does it mean to talk about restrictions, or projections, or joins (etc.) of relvars, as opposed to relations? Well, as I’ve written elsewhere (see, e.g., The Relational Database Dictionary, Extended Edition, Apress, 2008):
By definition, the operators projection, join, and so on apply to relation values specifically. In particular, of course, they apply to the values that happen to be the current values of relvars. It thus clearly makes sense to talk about, e.g., the projection of relvar S on attributes {CITY,STATUS}, meaning the relation that results from taking the projection on those attributes of the relation that’s the current value of that relvar S. In some contexts, however (normalization, for example), it turns out to be convenient to use expressions like “the projection of relvar S on attributes {CITY,STATUS}” in a slightly different sense. To be specific, we might say, loosely but very conveniently, that some relvar, CT say, is the projection of relvar S on attributes {CITY,STATUS}—meaning, more precisely, that the value of relvar CT at all times is the projection on those attributes of the value of relvar S at the time in question. In a sense, therefore, we can talk in terms of projections of relvars per se, rather than just in terms of projections of current values of relvars. Analogous remarks apply to all of the relational operations.
In other words, we do often talk in terms of (e.g.) restricting relvars as such; in particular, we do so in the context at hand. Such a manner of speaking is somewhat inappropriate—not to say sloppy—but it is at least succinct.
My second point is this. Among other things, I’ve considered the case in which S is a base relvar and LS and NLS are (restriction) views of that base relvar. For completeness, I ought really also to consider the inverse situation, in which LS and NLS are base relvars and S is a view of those relvars. But then S would be a union view, and so I’ll defer discussion of this case to Chapter 10, where I’ll be discussing union views in general. For now, let me just note the point that, in a sense, updating through union and updating through restriction are two sides of the same coin.
I’d like to close by reminding you of the following remarks (slightly paraphrased here) from the end of Chapter 1. As I said in that chapter, the conclusions from the motivating example are all rather obvious;[67] however, what I’m suggesting is that thinking of views as base relvars “living alongside” the relvars in terms of which they’re defined (as it were) is a fruitful way to think about the view updating problem in general—indeed, not just a fruitful way, but a way that I believe is logically correct. The basic idea is thus as follows: First, the view defining expressions imply certain constraints; second, such constraints in turn imply certain compensatory actions. To say it one more time, it’s not my intent that those actions should have to be specified explicitly by the DBA.
[52] Under the proposals of the paper “Inclusion Dependencies and Foreign Keys,” in Database Explorations: Essays on The Third Manifesto and Related Topics, by Hugh Darwen and myself (Trafford, 2010), we could say {SNO} in relvar S is a foreign key as well, referencing the key {SNO} of the disjoint union of relvars LS and NLS.
[53] In Chapter 2 I suggested as a rule of thumb that the predicates for relvars that are supposed to be disjoint should be so formulated as to preclude the possibility that any tuple might ever satisfy them both. Observe how I’ve applied that rule here to the predicates for LS and NLS in particular.
[54] The constraints are expressed in Tutorial D, of course, but for simplicity I’ve omitted the constraint names that Tutorial D would in fact require.
[55] It goes without saying—I hope!—that I’m not irrevocably wedded to that syntax. It’s sufficient for my purpose in this book, that’s all.
[56] E,g., as follows: ON <any update> TO S : LS := S WHERE CITY = ‘London’, NLS := S WHERE CITY ≠ ‘London’. Now, you might think this style for formulating rules is attractive, if only because it seems to be much simpler than the explicit INSERT and DELETE formulations that I prefer. However, my own opinion is that such simplification is mostly spurious. Certainly it makes it more difficult to examine certain pragmatically important issues, such as how to respond to a “pure INSERT” or “pure DELETE” request.
[57] Observe that this state of affairs exactly parallels that in which a user who sees both relvar S and relvar SP is allowed to perform (say) delete operations on relvar S, if those operations cascade to relvar SP.
[58] I apologize for my use of the slightly illogical term fixpoint here. It’s not my coinage. More important, note the tacit assumptions (a) that a fixpoint will indeed be reached, and moreover (b) that it’s unique! To repeat, I believe this aspect requires more study.
[59] One reviewer commented at this point that to use triggers in this way would be (a) highly nontrivial in general and (b) actually impossible in some cases, if the system in question doesn’t allow triggers to be invoked recursively.
[60] At least, they’re logically required so long as we have information equivalence.
[61] To spell the point out, we surely don’t want the overhead of first doing some deletes and then doing some inserts that effectively undo those deletes again.
[62] In SQL, such a rule would be more simply (?) defined by means of a specification of the form ON DELETE CASCADE, included, a trifle illogically, as part of the CREATE TABLE statement for table SP. (I say “illogically” because the delete that’s referred to in that specification is a delete on table S, not table SP.) I prefer a definition that (a) uses my own deliberately verbose syntax and (b) stands alone as a separate statement in its own right.
[63] More accurately, the constraints are derived from the view definitions, and the compensatory actions are then derived from those constraints.
[64] See, e.g., Using the New DB2: IBM’s Object-Relational Database System, by Don Chamberlin (Morgan Kaufmann, 1996).
[65] Observe that once again we’re dealing with a situation in which information equivalence holds (in particular, relvar S is equal to the union of relvars NLS and NPS, though this time the union isn’t disjoint). Note, incidentally that the predicates for NLS and NPS violate the discipline suggested in Chapter 2 (in a footnote) to the effect that the predicates for relvars R1 and R2 should preferably be such as to preclude the possibility that the same tuple might satisfy both.
[66] Although I’ve said that in practice insert and delete rules can be combined, I’ll continue to show them separately for reasons of clarity, most of the time.
[67] Obvious they might be, but (as we’ve seen) they do differ in certain respects from what might have been expected, and might in fact have occurred, given traditional approaches to view updating. For example, in SQL, an attempt to change the supplier city for some supplier in view LS will succeed (and will effectively cause the supplier in question to migrate to view NLS), unless view LS was explicitly defined WITH CHECK OPTION.
Get View Updating and Relational Theory now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.