Visualizing Data

Chapter 4. Time Series

The time series is a ubiquitous type of data set. It describes how some measurable feature (for instance, population, snowfall, or items sold) has changed over a period of time. Edward Tufte credits Johann Heinrich Lambert with the formal introduction of the time series to scientific literature in the 1700s.^[2]

Because of its ubiquity, the time series is a good place to start when learning about visualization. With it we can cover:

Acquiring a table of data from a text file
Parsing the contents of the file into a usable data structure
Calculating the boundaries of the data to facilitate representation
Finding a suitable representation and considering alternatives
Refining the representation with consideration for placement, type, line weight, and color
Providing a means of interacting with the data so that we can compare variables against one another or against the average of the whole data set

For a straightforward data set, let’s turn to the U.S. Department of Agriculture (USDA) for statistics on beverage consumption. Government sites are a terrific resource for data; see Chapter 9 for more information about them and other sources of data.

Most methods will be implemented “by hand” in this section. Further down the line, we’ll make generalized code to handle different scenarios, such as reading a table from a file or placing labels and grid lines on a plot.

Milk, Tea, and Coffee (Acquire and Parse)

The data set we use was originally downloaded from http://www.ers.usda.gov/data/foodconsumption/foodavailqueriable.aspx.

The page lets you define a query to download a data set of interest. The site claims that the data is in Excel format, but a glance at the contents of the resulting file shows that it’s only an HTML file with an .xls extension that fools Excel into opening it. Rather than getting into the specifics of how to download and clean the data, I offer an already processed version here:

http://benfry.com/writing/series/milk-tea-coffee.tsv

This data set contains three columns: the first for milk, the second for coffee, and the third for tea consumption in the United States from 1910 to 2004.

To read this file, use this modified version of the Table class from the previous chapter:

http://benfry.com/writing/series/floattable.pde

The modified version handles data stored as float values, making it more efficient than the previous version, which simply converted the data whenever getString( ), getFloat( ), or getInt( ) were used.

Open Processing and start a new sketch. Add both files to the sketch by either dragging each into the editor window or using Sketch → Add File.

Cleaning the Table (Filter and Mine)

It’s necessary to determine the minimum and maximum of each of the columns in the pre-filtered data set. These values are used to properly scale plotted points to locations on the screen.

The FloatTable class has methods for calculating the min and max for the rows and columns. These methods are worth discussing because they are important in later code. The following example calculates the minimum value for a column (comments denote important portions of the code):

  float getColumnMax(int col) {
    // Set the value of m to the lowest possible value,
    // so that the first value found will automatically be larger.
    float m = MIN_FLOAT;

    // Loop through each row.
    for (int row = 0; row < rowCount; row++) {

      // Only consider valid data elements (see later text).
      if (isValid(row, col)) {
        // Finally, check to see if the value
        // is greater than the maximum found so far.
        if (data[row][col] > m) {
          m = data[row][col];
        }
      }
    }
    return m;
  }

The isValid( ) method is important because most data sets have incomplete data. In the milk-tea-coffee.tsv file, all of the data is valid, but in most data sets (including others used in this chapter), missing values require extra consideration.

Because the values for milk, coffee, and tea will be compared against one another, it’s necessary to calculate the maximum value across all of the columns. The following bit of code does this after loading the milk-tea-coffee.tsv file:

FloatTable data;
float dataMin, dataMax;

void setup(  ) {
  data = new FloatTable("milk-tea-coffee.tsv");

  dataMin = 0;
  dataMax = data.getTableMax(  );
}

Sometimes, it’s also useful to calculate the minimum value, but setting the minimum to zero provides a more accurate comparison between the three data sets. The minimum for this data set is 5.1, and the values for the tea column hover around 6, so using 5.1 as the dataMin value would produce a chart that looked as though the beverage history included periods of no (or nearly no) tea consumption in the U.S. In addition, if the value is 6, it’s important that the relative difference seen by the viewer is not just 0.9, but that it shows the full range from 0 up to 5.1 and how it compares to a value of 6.

Each row name specifies a year, which will be used later to draw labels on the plot. To make them useful in code, it’s also necessary to get the minimum and maximum year after converting the entire group to an int array. The getRowNames( ) method inside FloatTable returns a String array that can be converted with the int( ) casting function:

FloatTable data;
float dataMin, dataMax;int yearMin, yearMax;
int[] years;

void setup(  ) {
  data = new FloatTable("milk-tea-coffee.tsv");
  years = int(data.getRowNames(  ));
  yearMin = years[0];
  yearMax = years[years.length - 1];

  dataMin = 0;
  dataMax = data.getTableMax(  );
}

A Simple Plot (Represent and Refine)

To begin the representation, it’s first necessary to set the boundaries for the plot location. The plotX1, plotY1, plotX2, and plotY2 variables define the corners of the plot. To provide a nice margin on the left, set plotX1 to 50, and then set the plotX2 coordinate by subtracting this value from width. This keeps the two sides even, and requires only a single change to adjust the position of both. The same technique is used for the vertical location of the plot:

FloatTable data;
float dataMin, dataMax;float plotX1, plotY1;
float plotX2, plotY2;

int yearMin, yearMax;
int[] years;


void setup(  ) {
  size(720, 405);

  data = new FloatTable("milk-tea-coffee.tsv");

  years = int(data.getRowNames(  ));
  yearMin = years[0];
  yearMax = years[years.length - 1];

  dataMin = 0;
  dataMax = data.getTableMax(  );

  // Corners of the plotted time series
  plotX1 = 50;
  plotX2 = width - plotX1;
  plotY1 = 60;
  plotY2 = height - plotY1;

  smooth(  );
}

Next, add a draw( ) method that sets the background to a light gray and draws a filled white rectangle for the plotting area. That will make the plot stand out against the background, rather than a color behind the plot itself—which can muddy its appearance.

The rect( ) function normally takes the form rect(x, y, width, height), but rectMode(CORNERS) changes the parameters to rect(left, top, right, bottom), which is useful because our plot’s shape is defined by the corners. Like other methods that affect drawing properties, such as fill( ) and stroke( ), rectMode( ) affects all geometry that is drawn after it until the next time rectMode( ) is called:

void draw(  ) {
  background(224);

  // Show the plot area as a white box.
  fill(255);
  rectMode(CORNERS);
  noStroke(  );
  rect(plotX1, plotY1, plotX2, plotY2);

  strokeWeight(5);
  // Draw the data for the first column.
  stroke(#5679C1);
  drawDataPoints(0);
}


// Draw the data as a series of points.
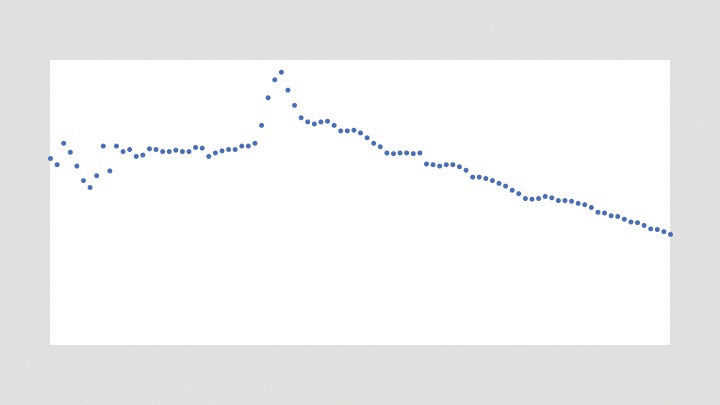
void drawDataPoints(int col) {
  int rowCount = data.getRowCount(  );
  for (int row = 0; row < rowCount; row++) {
    if (data.isValid(row, col)) {
      float value = data.getFloat(row, col);
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      float y = map(value, dataMin, dataMax, plotY2, plotY1);
      point(x, y);
    }
  }
}

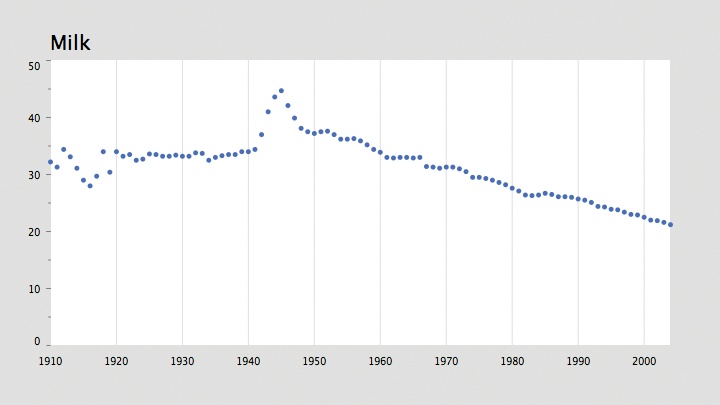
Because the data is drawn as points using the drawDataPoints( ) method, a stroke color and weight are set. This method also takes a column index to draw as a parameter. The results are in Figure 4-1. For the first step, I’ve shown only the first column of data (the values for milk consumption).

Figure 4-1. One set of points over time

The map( ) function does most of the work. The x coordinate is calculated by mapping the year for each row from yearMin and yearMax to plotX1 and plotX2. Another option would be to use the row variable, instead of the year:

float x = map(row, 0, rowCount-1, plotX1, plotX2);

But a value for row would be less accurate because a year or two might be missing from the data set, which would skew the representation. Again, this data set is complete, but often that is not the case.

Labeling the Current Data Set (Refine and Interact)

Missing from the previous code is an indicator of the currently visible column of data (whether milk, tea, or coffee) and a means to swap between each of the three. For this, we add a variable to keep track of the current column, and another for the font used for the title. And few lines of code are added to the draw( ) method to write the name of the column with the text( ) method:

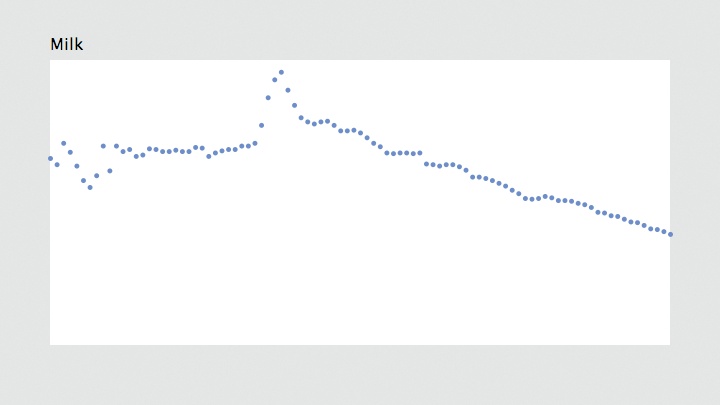
FloatTable data;
float dataMin, dataMax;

float plotX1, plotY1;
float plotX2, plotY2;int currentColumn = 0;
int columnCount;

int yearMin, yearMax;
int[] years;

PFont plotFont;


void setup(  ) {
  size(720, 405);
  data = new FloatTable("milk-tea-coffee.tsv");
  columnCount = data.getColumnCount(  );

  years = int(data.getRowNames(  ));
  yearMin = years[0];
  yearMax = years[years.length - 1];

  dataMin = 0;
  dataMax = data.getTableMax(  );

  // Corners of the plotted time series
  plotX1 = 50;
  plotX2 = width - plotX1;
  plotY1 = 60;
  plotY2 = height - plotY1;

  plotFont = createFont("SansSerif", 20);
  textFont(plotFont);

  smooth(  );
}


void draw(  ) {
  background(224);

  // Show the plot area as a white box.
  fill(255);
  rectMode(CORNERS);
  noStroke(  );
  rect(plotX1, plotY1, plotX2, plotY2);

  // Draw the title of the current plot.
  fill(0);
  textSize(20);
  String title = data.getColumnName(currentColumn);
  text(title, plotX1, plotY1 - 10);

  stroke(#5679C1);
  strokeWeight(5);
  drawDataPoints(currentColumn);
}

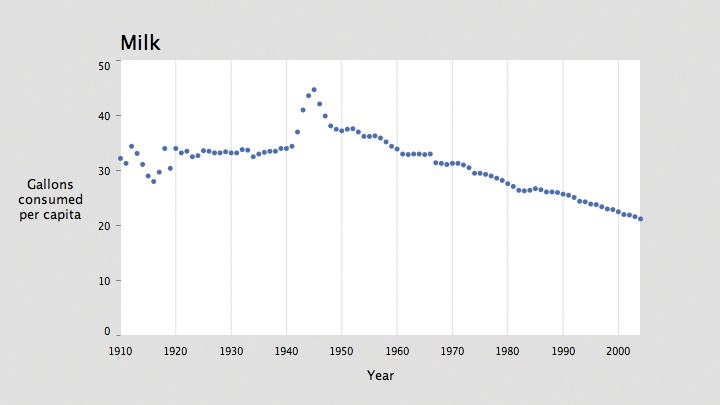
The text( ) line draws the text 10 pixels above plotY1, which represents the top of the plot, and the drawDataPoints( ) line uses currentColumn instead of just 0. Results are shown in Figure 4-2.

Figure 4-2. Time series with data set labeled

The createFont( ) function is used to create a font from one of the built-in typefaces. The built-in typefaces are Serif, SansSerif, Monospaced, Dialog, and DialogInput; they map to the default fonts on each operating system. On Mac OS X, for instance, SansSerif maps to Lucida Sans, whereas on Windows it maps to Arial. The default fonts are useful when you don’t want to deal with the Create Font tool, but the font choices are not particularly inspiring, and they don’t guarantee consistent output across different operating systems. For instance, making pixel-level decisions with a built-in font is a bad idea because the shaping and spacing of the characters can be significantly different on other operating systems.

One advantage of using createFont( ) is that the text will look smooth at any size, unlike a font used with loadFont( ), which may be distorted as it is resized.

It is possible to use createFont( ) to specify something besides a built-in font, but there’s no guarantee that the font will be installed on another user’s system. This can be useful for testing, after which you can use the Create Font tool before deployment. The name of a font used by createFont( ) should be identical to how it is listed in the Create Font tool. You can also get a list of the available fonts with the PFont.list( ) method, which returns a String array. The following will print the list of all available fonts to the console:

println(PFont.list(  ));

Tip

If you have a lot of fonts installed on your system, there might be a long delay before they are listed.

The createFont( ) method can also be used with a TrueType (.ttf) or OpenType (.otf) file added to the data folder. Most TrueType fonts will work, but OpenType support varies by platform. Be mindful of copyrighted fonts when using this method in a sketch for public distribution.

A simple means of swapping between columns of data is to add a keyPressed( ) method, which will automatically run any time a key is pressed:

void keyPressed(  ) {
  if (key == '[') {
    currentColumn--;
    if (currentColumn < 0) {
      currentColumn = columnCount - 1;
    }
  } else if (key == ']') {
    currentColumn++;
    if (currentColumn == columnCount) {
      currentColumn = 0;
    }
  }
}

This method will rotate through the columns as the user presses the [ and ] (bracket) keys. When the number gets too big or too small, it wraps around to the beginning or end of the list. Because columnCount is 3, the possible currentColumn values are 0, 1, and 2. So, when currentColumn reaches a value less than zero, it wraps around to 2 (columnCount - 1).

Drawing Axis Labels (Refine)

An unlabeled plot has minimal utility. It clearly displays relative up or down swings, but without a sense of the time period or amounts to indicate the degree of swing, it’s impossible to know whether values have changed by, say, 5% or 50%. And some indication is required to explain that the horizontal axis represents the year and the vertical axis represents actual volumes: the amount consumed of a particular beverage, measured in gallons per capita per year.

There are clever (and complicated) means of selecting intervals, but for this project, we will pick the interval by hand. Choosing a proper interval and deciding whether to include major and minor tick marks depends on the data, but a general rule of thumb is that five intervals is at the low end, and more than ten is likely a problem. Too many labels make the diagram look like graph paper, and too few suggests that only the minimum and maximum values need to be shown.

The most important consideration is the way the data is used. Are minute, year-by-year comparisons needed? Always use the fewest intervals you can get away with, as long as the plot shows the level of detail the reader needs. Sometimes no labels are necessary—if values are only meant to be compared against one another. For instance, you might dispense with labels if you want to show only upward and downward trends. Other factors, such as the width of the plot, also play a role, so determining the correct level of detail usually requires a little trial and error.

Year Labels

Creating the year axis is straightforward. The data ranges from 1910 to 2004, so an interval of 10 years means marking 10 individual years: 1910, 1920, 1930, and so on, up to 2000. Add the yearInterval variable to the beginning of the code before setup( ):

int yearInterval = 10;

Next, add the following function to draw the year labels:

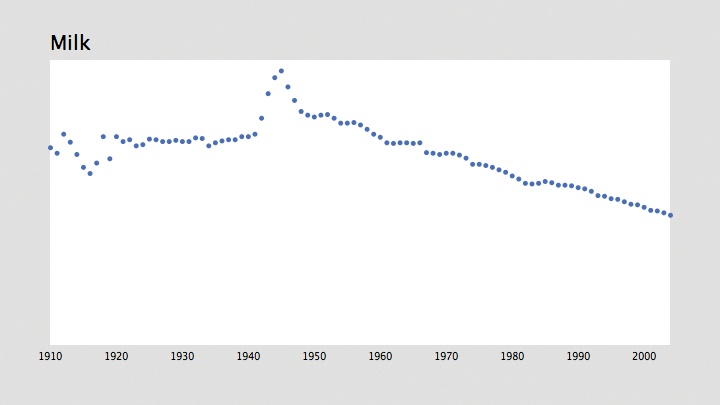
void drawYearLabels(  ) {
  fill(0);
  textSize(10);
  textAlign(CENTER, TOP);
  for (int row = 0; row < rowCount; row++) {
    if (years[row] % yearInterval == 0) {
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      text(years[row], x, plotY2 + 10);
    }
  }
}

The fill color is set to black, the text size to 10, and the alignment to the middle so that the year number centers on the position of the data point for that year.

Two lines in this code deserve further consideration. The first is the line that makes use of the %, or modulo, operator. A modulo operation returns the remainder from a division. So, for example, 7 % 2 is equal to 1, and 8 % 5 equals 3. It’s useful for drawing labels because it provides a way to easily identify a year ending in 0. Dividing 1910 by 10 returns 0, so a label is drawn, whereas dividing 1911 by 10 produces 1, and so it continues until the loop reaches 1920, which also returns 0 when divided by 10.

A second parameter to textAlign( ) sets the vertical alignment of the text. The options are TOP, BOTTOM, CENTER, and BASELINE (the default). The TOP and CENTER parameters are straightforward. The BOTTOM parameter is the same as BASELINE when only one line of text is used, but for multiple lines, the final line will be aligned to the baseline, with the previous lines appearing above it. When only one parameter is used, the vertical alignment resets to BASELINE.

The resulting image is shown in Figure 4-3.

Figure 4-3. Time series with labeled x-axis

Tip

To draw text that does not bump into the elements above it, you need to know the height of the tallest character in the font. Typographers refer to this as the ascent. Traditionally, the ascent of a font is the height to the top of a capital H character. Characters such as the capital O or a capital B are in fact slightly taller than the letter H and dip slightly below the baseline—the bottom line from which text is drawn. The ascent value essentially refers to the optical height of the font, which is the height perceived by our eyes.

Simple grid lines can also help the presentation by identifying each interval. The following modifications add a grid to the drawYearLabels( ) function:

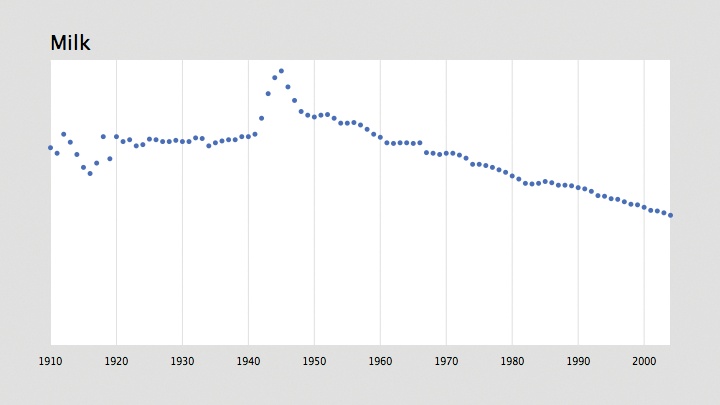
void drawYearLabels(  ) {
  fill(0);
  textSize(10);
  textAlign(CENTER, TOP);// Use thin, gray lines to draw the grid.
  stroke(224);
  strokeWeight(1);

  for (int row = 0; row < rowCount; row++) {
    if (years[row] % yearInterval == 0) {
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      text(years[row], x, plotY2 + 10);
      line(x, plotY1, x, plotY2);
    }
  }
}

Figure 4-4 shows the result.

Figure 4-4. Time series with vertical grid

Notice that because the fill color does not affect lines, and a stroke color does not affect text, it is not necessary to use noFill( ) or noStroke( ) in this method.

With a separate method to draw the year labels, it makes sense to put the code that draws the title into its own method. The drawTitle( ) method takes this code from the draw( ) function. Just replace the title drawing code inside draw( ) with:

drawTitle(  );

and then add the following method to the code:

void drawTitle(  ) {
  fill(0);
  textSize(20);
  textAlign(LEFT);
  String title = data.getColumnName(currentColumn);
  text(title, plotX1, plotY1 - 10);
}

Because the drawYearLabels( ) function changes the text alignment, a line is added to reset to textAlign(LEFT) before drawing the title. Otherwise, the title would appear centered at plotX1 on the next trip through the draw( ) method, inheriting the text alignment settings from the previous draw( ).

Labeling Volume on the Vertical Axis

The vertical axis can be handled the same way as the horizontal, but it is a bit trickier. A quick println(dataMax) added to setup( ) tells us that the maximum value is 46.4. Intervals of 10 will again suffice, this time producing only 5 divisions (as opposed to 10 in the horizontal):

int volumeInterval = 10;

With a dataMax value of 46.4 and intervals of 10, rounding up dataMax to the nearest interval will make the maximum value on the plot 50, making it a little easier to read changes in vertical values. To do so automatically, divide dataMax by volumeInterval. The result is 4.64. Next, use ceil( ), which rounds a float up to the next int value (in this case, 5), called the ceiling of a float. Then, set dataMax to the rounded value multiplied by volumeInterval. That calculation took a few sentences to explain, but the code consists of a one-line change to setup( ):

dataMax = ceil(data.getTableMax(  ) / volumeInterval) * volumeInterval;

To draw the labels, create a loop that iterates from the minimum to maximum data values. Use an increment of volumeInterval to draw a label at each interval:

void drawVolumeLabels(  ) {
  fill(0);
  textSize(10);
  textAlign(RIGHT, CENTER);

  for (float v = dataMin; v <= dataMax; v += volumeInterval) {
    float y = map(v, dataMin, dataMax, plotY2, plotY1);
    text(floor(v), plotX1 - 10, y);
  }
}

Add a draw VolumeLabels( ) call to the draw( ) method, next to drawTitle( ). When you’re drawing the text label, the floor( ) function removes decimals from the number value because there’s no need to write 10.0, 20.0, 30.0, etc. when 10, 20, and 30 will suffice. If dataInterval included decimal points, the nf( ) method could be used instead to format the value to a specific number of decimal places.

Tip

The text( ) method can draw int or float values instead of just String objects. For float values, it is best to use the nf( ) method to first convert the float to a specific number of decimal places. By default, text( ) will format a float to three decimal places. That is different from Java, which can have many digits in the decimal place for a float, because using just a few digits is usually more useful for a graphical display. To get the full 4-, 8-, or 15-digit version of the float value, use the str( ) function to convert the float to a String. For Java programmers, using str( ) is equivalent to String.valueOf( ).

The x-coordinate of the label text is the lefthand edge of the plot minus a few pixels. Also note the use of textAlign( ) to vertically center the text.

With the vertical centering, the label drawn at 0 is visually a little too close to the year markers below. In its current state, this example is not detailed enough to be used for real analysis and is better at showing upward and downward trends. In that context, it’s clear from a glance that the bottom of the plot is 0, so the bottom label could be left out completely. The same goes for the top value, which gets close to the title. To leave these out, alter the first value drawn by adding a volumeInterval to dataMin, and end the loop at v < dataMax instead of v <= dataMax so that the 50 won’t be drawn:

void drawVolumeLabels(  ) {
  fill(0);
  textSize(10);
  textAlign(RIGHT, CENTER);float dataFirst = dataMin + volumeInterval;
  for (float v = dataFirst; v < dataMax; v += volumeInterval) {
    float y = map(v, dataMin, dataMax, plotY2, plotY1);
    text(floor(v), plotX1 - 10, y);
  }
}

In other cases, it might not be appropriate to remove upper and lower values. If dataMin were something other than 0, or the intervals more awkward than simple intervals of 10, viewers might be confused without the minimum and maximum values. In such cases, the maximum value (50) can be vertically aligned to the top of the plot, and the minimum value (0) to the bottom, rather than centered vertically like the rest of the labels:

void drawVolumeLabels(  ) {
  fill(0);
  textSize(10);for (float v = dataMin; v <= dataMax; v += volumeInterval) {
    float y = map(v, dataMin, dataMax, plotY2, plotY1);
    if (v == dataMin) {
      textAlign(RIGHT); // Align by the bottom
    } else if (v == dataMax) {
      textAlign(RIGHT, TOP); // Align by the top
    } else {
      textAlign(RIGHT, CENTER); // Center vertically
    }
    text(floor(v), plotX1 - 10, y);
  }
}

Horizontal lines can be fashioned in the same manner as those for the year. Choosing whether to use a horizontal or vertical grid depends on the axis with data that is most important to be measured. If this plot is being used to analyze exact changes in milk consumption, the horizontal gridlines will better help with identifying changes. But if the purpose is to compare upward and downward trends across different years (for instance, to understand how milk consumption changed during and after World War II), the vertical gridlines are more valuable. For this data set, it’s most interesting to compare changes over the years, so we’ll stick with vertical lines.

Instead of gridlines, small tick marks near the labels on the vertical axis can be produced with the same technique, by drawing a short line just outside the edge of the plot. Minor gridlines or tick marks can be drawn by including a variable for a second interval that’s a multiple of the first and incrementing by that interval in the loop. The following modification to drawVolumeLabels( ) adds major and minor tick marks to the volume axis:

int volumeIntervalMinor = 5; // Add this above setup(  )void drawVolumeLabels(  ) {
  fill(0);
  textSize(10);stroke(128);
  strokeWeight(1);

  for (float v = dataMin; v <= dataMax; v += volumeIntervalMinor) {
    float y = map(v, dataMin, dataMax, plotY2, plotY1);
    if (v % volumeInterval == 0) { // If a major tick mark
      if (v == dataMin) {
        textAlign(RIGHT); // Align by the bottom
      } else if (v == dataMax) {
        textAlign(RIGHT, TOP); // Align by the top
      } else {
        textAlign(RIGHT, CENTER); // Center vertically
      }
      text(floor(v), plotX1 - 10, y);
      line(plotX1 - 4, y, plotX1, y); // Draw major tick
     } else {
      line(plotX1 - 2, y, plotX1, y); // Draw minor tick
    }
    }
  }

The result with the tick marks and vertical labels is shown in Figure 4-5.

Figure 4-5. Tick marks on the vertical axis

Strictly speaking, the minor tickmarks in this example are not very informative. They can be removed to avoid visual clutter; simply comment out the line that draws the minor ticks.

Bringing It All Together and Titling Both Axes

So far, anyone looking at this diagram should be able to guess that it has something to do with milk from 1910 to sometime after 2000. To further explain the plot, the next step is to provide titles for the year and volume axes. Informative axis titles are important for the people viewing your data.

The year axis title is simple: just a piece of text centered between plotX1 and plotX2. After centering the text in both directions with textAlign(CENTER, CENTER), the text is drawn centered between plotY1 and plotY2. To fit both, the values for plotX1 and friends must be changed to make room for the labels. In this case, eyeballing the placement is sufficient, though textWidth( ) could be used to accurately size the lefthand margin, and textAscent( ) could do the same for the label below.

For the vertical axis, it might be tempting to rotate the title on its side, but more often than not it is more effective at giving your viewer eyestrain than it is at communicating. I’ve kept the text horizontal and broken the label into three lines by inserting newline characters (\n) into the string.

Figure 4-6 shows our progress.

Figure 4-6. Axis labels

Here’s the code listing for the program thus far, with the lines highlighted that were altered to display the titles:

FloatTable data;
float dataMin, dataMax;
float plotX1, plotY1;
float plotX2, plotY2;float labelX, labelY;

int rowCount;
int columnCount;
int currentColumn = 0;

int yearMin, yearMax;
int[] years;

int yearInterval = 10;
int volumeInterval = 10;
int volumeIntervalMinor = 5;

PFont plotFont;


void setup(  ) {
  size(720, 405);

  data = new FloatTable("milk-tea-coffee.tsv");
  rowCount = data.getRowCount(  );
  columnCount = data.getColumnCount(  );

  years = int(data.getRowNames(  ));
  yearMin = years[0];
  yearMax = years[years.length - 1];

  dataMin = 0;
  dataMax = ceil(data.getTableMax(  ) / volumeInterval) * volumeInterval;

  // Corners of the plotted time series
  plotX1 = 120;
  plotX2 = width - 80;
  labelX = 50;
  plotY1 = 60;
  plotY2 = height - 70;
  labelY = height - 25;

  plotFont = createFont("SansSerif", 20);
  textFont(plotFont);

  smooth(  );
}


void draw(  ) {
  background(224);

  // Show the plot area as a white box
  fill(255);
  rectMode(CORNERS);
  noStroke(  );
  rect(plotX1, plotY1, plotX2, plotY2);
  drawTitle(  );
  drawAxisLabels(  );

  drawYearLabels(  );
  drawVolumeLabels(  );

  stroke(#5679C1);
  strokeWeight(5);
  drawDataPoints(currentColumn);
}


void drawTitle(  ) {
  fill(0);
  textSize(20);
  textAlign(LEFT);
  String title = data.getColumnName(currentColumn);
  text(title, plotX1, plotY1 - 10);
}


void drawAxisLabels(  ) {
  fill(0);
  textSize(13);
  textLeading(15);

  textAlign(CENTER, CENTER);
  // Use \n (aka enter or linefeed) to break the text into separate lines.
  text("Gallons\nconsumed\nper capita", labelX, (plotY1+plotY2)/2);
  textAlign(CENTER);
  text("Year", (plotX1+plotX2)/2, labelY);
}


void drawYearLabels(  ) {
  fill(0);
  textSize(10);
  textAlign(CENTER, TOP);

  // Use thin, gray lines to draw the grid.
  stroke(224);
  strokeWeight(1);

  for (int row = 0; row < rowCount; row++) {
    if (years[row] % yearInterval == 0) {
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      text(years[row], x, plotY2 + 10);
      line(x, plotY1, x, plotY2);
    }
  }
}

void drawVolumeLabels(  ) {
  fill(0);
  textSize(10);
  stroke(128);
  strokeWeight(1);

  for (float v = dataMin; v <= dataMax; v += volumeIntervalMinor) {
    float y = map(v, dataMin, dataMax, plotY2, plotY1);
    if (v % volumeInterval == 0) { // If a major tick mark
      if (v == dataMin) {
        textAlign(RIGHT); // Align by the bottom
      } else if (v == dataMax) {
        textAlign(RIGHT, TOP); // Align by the top
      } else {
        textAlign(RIGHT, CENTER); // Center vertically
      }
      text(floor(v), plotX1 - 10, y);
      line(plotX1 - 4, y, plotX1, y); // Draw major tick
    } else {
      // Commented out; too distracting visually
      //line(plotX1 - 2, y, plotX1, y); // Draw minor tick
    }
  }
 }


void drawDataPoints(int col) {
  for (int row = 0; row < rowCount; row++) {
    if (data.isValid(row, col)) {
      float value = data.getFloat(row, col);
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      float y = map(value, dataMin, dataMax, plotY2, plotY1);
      point(x, y);
    }
  }
}


void keyPressed(  ) {
  if (key == '[') {
    currentColumn--;
    if (currentColumn < 0) {
      currentColumn = columnCount - 1;
    }
  } else if (key == ']') {
    currentColumn++;
    if (currentColumn == columnCount) {
      currentColumn = 0;
    }
  }
}

Choosing a Proper Representation (Represent and Refine)

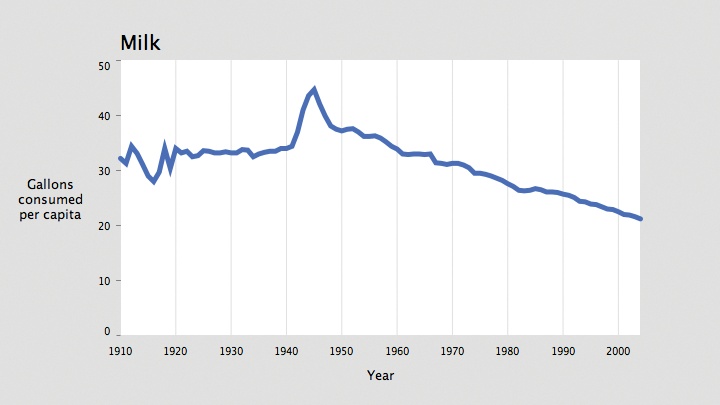
A series of points can be difficult to follow if they’re not connected. It’s not as easy to compare milk and coffee in these images, for instance, because the predominant difference between the two plots is that the coffee values are far more erratic than those for milk. Instead of a specific shape, the points make an indeterminate cloud that is difficult to make sense of at a quick glance.

When values are truly a series and there is no missing data, it’s possible to use a line graph and simply connect the points. The beginShape( ) and endShape( ) methods provide a means for drawing irregular shapes. The vertex( ) method adds a single point to the shape. To connect the dots in a line, replace the point( ) method with vertex( ).

Three examples follow that show the basic drawing modes of beginShape( ) and endShape( ). See Figure 4-7. Using noFill( ) will produce the image at left, and the default fill and stroke settings will produce the image in the center. The CLOSE parameter in the endShape( ) method handles the connection of the final point to the first, so that the stroke completely outlines the shape. Always use endShape(CLOSE) when closing a shape because the alternative—repeating the first point—may cause unexpected visual defects.

Figure 4-7. Examples using beginShape( ) and endShape( )

// Leftmost image: fill disabled and the default stroke
noFill(  );
beginShape(  );
vertex(10, 10);
vertex(90, 30);
vertex(40, 90);
vertex(50, 40);
endShape(  );

// Center image: default fill (white) and stroke (black)
beginShape(  );
vertex(10, 10);
vertex(90, 30);
vertex(40, 90);
vertex(50, 40);
endShape(  );
// Rightmost image: default fill and stroke, closed shape
beginShape(  );
vertex(10, 10);
vertex(90, 30);
vertex(40, 90);
vertex(50, 40);
endShape(CLOSE);

To represent a time series, we want a simple line with no fill, so we’ll use the nofill( ) form of the shape. The following method is a variation of drawPoints( ) that draws the data with beginShape( ) and endShape( ), with the alterations highlighted:

void drawDataLine(int col) {
  beginShape(  );  int rowCount = data.getRowCount(  );
  for (int row = 0; row < rowCount; row++) {
    if (data.isValid(row, col)) {
      float value = data.getFloat(row, col);
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      float y = map(value, dataMin, dataMax, plotY2, plotY1);vertex(x, y);
    }
  }
  endShape(  );
}

Inside draw( ), comment out the line that reads:

  drawDataPoints(currentColumn);

by placing a pair of slashes (//) in front of it. On the line that follows, add:

  noFill(  );
  drawDataLine(currentColumn);

The noFill( ) command is important; without it, the shape would have a strange black background because the fill was last set to black in the prior lines that draw the text label for the plot. This version of the code produces the image shown in Figure 4-8.

Figure 4-8. Continuously drawn time series using vertices

It could also be used to draw all three series (milk, tea, and coffee) on a single plot. To do this, call drawDataLine( ) once for each of the three columns, and set a different stroke color for each.

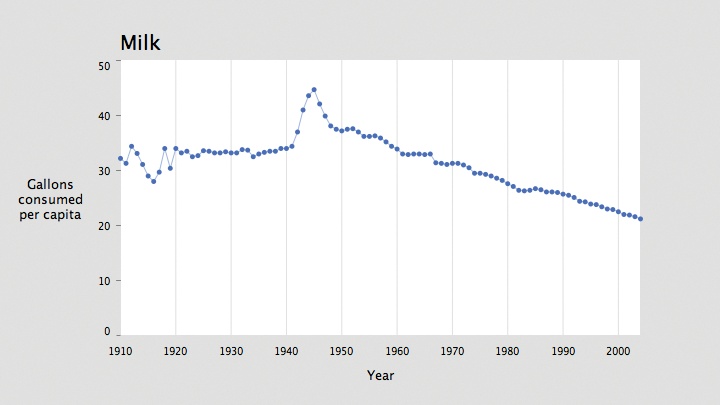
It’s also easy to mix lines and points in the representation to create a background line that highlights the individual data points. To do so, set the stroke weight to something smaller while drawing the lines and keep the thicker weight for the points. Modify the end of draw( ) to read as follows:

  stroke(#5679C1);
  strokeWeight(5);
  drawDataPoints(currentColumn);
  noFill(  );
  strokeWeight(0.5);
  drawDataLine(currentColumn);

The result appears in Figure 4-9.

Figure 4-9. Combined dots and continuous line

Note that the functions themselves should not be merged, as other shape commands (such as point( )) are not permitted inside a beginShape( ) and endShape( ) block.

Depending on how you use this code, it may be important to draw the points after the lines. For example, if you set the stroke of the line to a light gray, it would be best to draw the blue points on top of the line so that the points are not bisected by an odd gray line (which has poor contrast with blue).

Using Rollovers to Highlight Points (Interact)

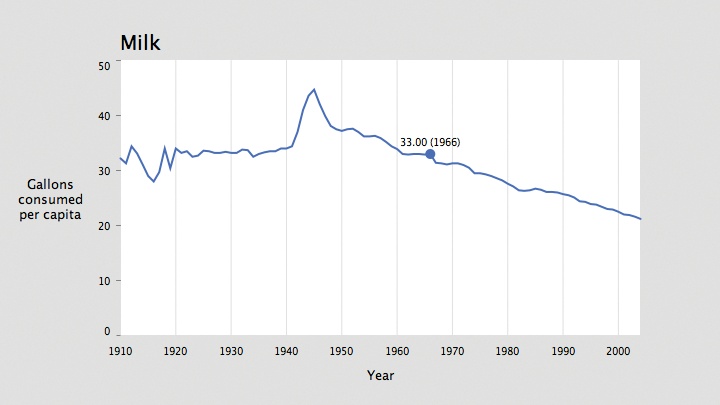
The lines and points combination is overkill for this data set: there are so many data points horizontally that the individual dots (at a size of five pixels) are nearly the size of the space allotted for each data point (around seven pixels), leaving only two pixels between them. Another option is to highlight individual points when the mouse is nearby. This is technique is nearly identical to the one used at the end of the previous chapter, and the function looks like the following:

void drawDataHighlight(int col) {
  for (int row = 0; row < rowCount; row++) {
    if (data.isValid(row, col)) {
      float value = data.getFloat(row, col);
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      float y = map(value, dataMin, dataMax, plotY2, plotY1);
      if (dist(mouseX, mouseY, x, y) < 3) {
        strokeWeight(10);
        point(x, y);
        fill(0);
        textSize(10);
        textAlign(CENTER);
        text(nf(value, 0, 2) + " (" + years[row] + ")", x, y-8);
      }
    }
  }
}

The stroke weight for the point is set to 10 because the weight used in the drawDataPoints( ) method (5) would not contrast enough with the rest of the image. Similarly, the stroke weight for the lines is set to 2, rather than the 0.5 stroke used when combining drawDataLines( ) and drawDataPoints( ), because it should stand out more. But strokeWeight(2) is still thinner than the strokeWeight(5) used when the drawDataLines( ) method is run by itself because if the line itself is too thick, the rollover won’t be prominent enough.

The modified draw( ) method to draw the highlight follows:

void draw(  ) {
  background(224);

  // Show the plot area as a white box.
  fill(255);
  rectMode(CORNERS);
  noStroke(  );
  rect(plotX1, plotY1, plotX2, plotY2);
  drawTitle(  );
  drawAxisLabels(  );

  drawYearLabels(  );
  drawVolumeLabels(  );

  stroke(#5679C1);noFill(  );
  strokeWeight(2);
  drawDataLine(currentColumn);
  drawDataHighlight(currentColumn);
}

An image of the result is shown in Figure 4-10.

Figure 4-10. Time series with user-selected highlight

Ways to Connect Points (Refine)

Connecting the points with a curve is often a better option because it prevents the spikiness of the plot from overwhelming the data itself. The curveVertex( ) function is similar to the vertex( ) function, except that it connects successive points by fitting them to a curve.

The drawDataCurve( ) method, a modification of drawDataLine( ), follows:

void drawDataCurve(int col) {
  beginShape(  );
  for (int row = 0; row < rowCount; row++) {
    if (data.isValid(row, col)) {
      float value = data.getFloat(row, col);
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      float y = map(value, dataMin, dataMax, plotY2, plotY1);curveVertex(x, y);
      // Double the curve points for the start and stop
      if ((row == 0) || (row == rowCount-1)) {
        curveVertex(x, y);
      }
    }
  }
  endShape(  );
}

To draw a curve with curveVertex( ), at least four points are necessary because the first and last coordinates in curveVertex( ) are used to guide the angle at which the curve begins and ends. In this particular example, doubling start and stop points will work fine. In other cases, additional points can be used to maintain continuity between two connected curves.

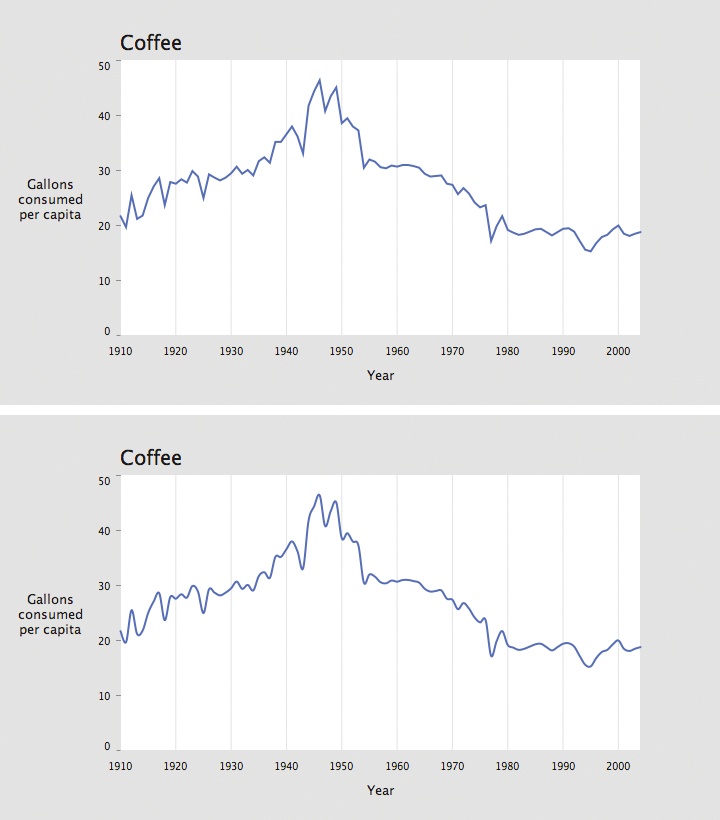
The results of using a smooth curve can be seen most clearly when comparing the coffee data drawn with vertex( ) and curveVertex( ) in Figure 4-11.

Figure 4-11. Comparison of the use of vertices (top) and curve vertices (bottom)

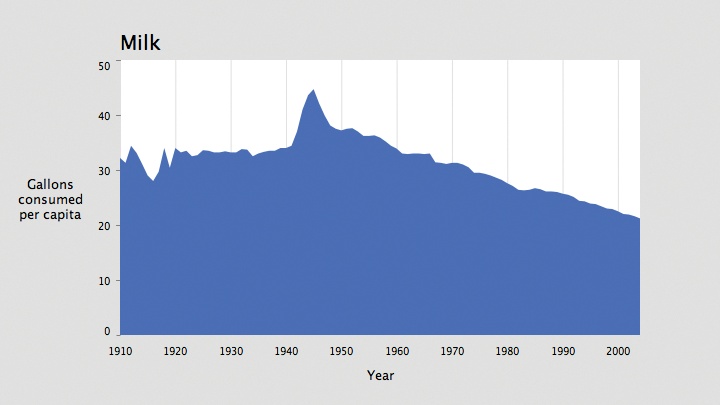
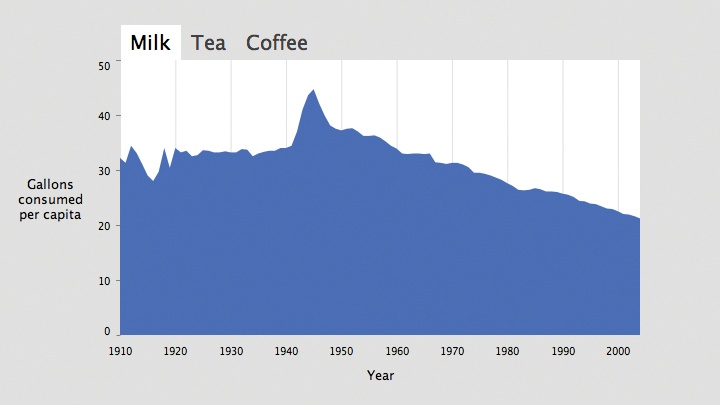
Showing Data As an Area

Another variation of drawDataLine( ) draws the values as a filled area. Before calling endShape( ), add the lower-right corner and then the lower-left corner to complete the outline of the shape to be filled. And instead of endShape( ) with no parameters, use endShape(CLOSE) to close it, reconnecting it to the first vertex.

The new drawDataArea( ) function is:

void drawDataArea(int col) {  beginShape(  );
  for (int row = 0; row < rowCount; row++) {
    if (data.isValid(row, col)) {
      float value = data.getFloat(row, col);
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      float y = map(value, dataMin, dataMax, plotY2, plotY1);
      vertex(x, y);
    }
  }// Draw the lower-right and lower-left corners.
  vertex(plotX2, plotY2);
  vertex(plotX1, plotY2);
  endShape(CLOSE);
}

Next, modify the end of the draw( ) method to replace the stroke(#5679C1) line with fill(#5679C1), and change noFill( ) to noStroke( ); drawing an outline around an already filled shape is unnecessary:

  noStroke(  );
  fill(#5679C1);
  drawDataArea(currentColumn);

The new plot is shown in Figure 4-12.

Figure 4-12. Filled time series

This makes a more attractive plot, and because the data set considers the actual volume of consumption—that is, the vertical axis starts at 0—it makes sense to fill the area beneath the data points. Whenever filling a plot, consider whether the data being shown refers to some kind of actual area or volume. For instance, it would not be appropriate to fill the area beneath a plot of temperature because the lower bound is arbitrary (unless you’re measuring temperatures above absolute zero). A graph of rainfall, however, refers to the actual volume or amount that can be measured upward from “none,” making it a candidate for a filled plot.

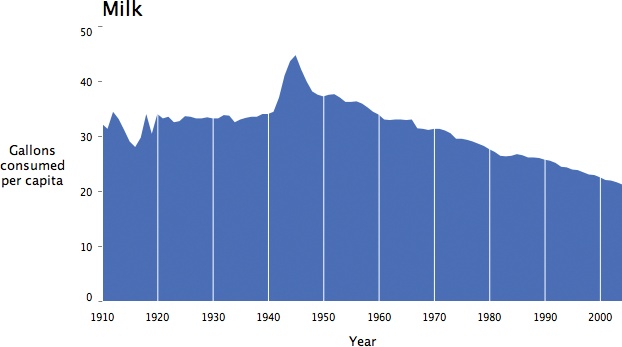
Further Refinements and Erasing Elements

The highest priority of any information graphic is to place the data it represents first and foremost. A filled area can seem too much like the background, so sometimes it’s best to remove the background. Without the gray background, the grid lines become awkward without some kind of box around them to contain the plot. A box adds no additional usefulness, just clutters the composition, so a better option is to remove the background and make the gridlines part of the graphic itself by setting their color to white. To draw the gridlines on top of the data, move the drawYearLabels( ) method after drawDataArea( ) inside draw( ) so that the grid lines will be drawn after the filled shape. The new draw( ) method is very sparse:

void draw(  ) {
  background(255);

  drawTitle(  );
  drawAxisLabels(  );
  drawVolumeLabels(  );

  noStroke(  );
  fill(#5679C1);
  drawDataArea(currentColumn);

  drawYearLabels(  );
}

Inside drawYearLabels( ), use stroke(255) instead of stroke(224) to make the gridlines white. The results are shown in Figure 4-13.

Figure 4-13. Unboxed plot with reverse-color gridlines

Such minimization of graphic elements has long been the province of those who champion a “less is more” approach to design. Edward Tufte later popularized this approach in his series of books on information graphics.

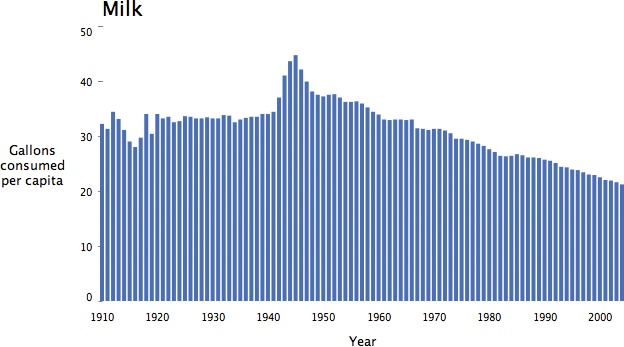
Discrete Values with a Bar Chart (Represent)

When values are discrete and cannot be shown in a series, a bar chart might be more suitable. A common example is when data is missing and therefore does not represent a complete series. Drawing a bar chart is a matter of using rectangles instead of individual points, and then drawing the data centered at each horizontal location.

The following replacement for drawDataArea( ) creates a bar chart:

float barWidth = 4; // Add to the top of the page, before setup(  )

void drawDataBars(int col) {  noStroke(  );rectMode(CORNERS);

  for (int row = 0; row < rowCount; row++) {
    if (data.isValid(row, col)) {
      float value = data.getFloat(row, col);
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      float y = map(value, dataMin, dataMax, plotY2, plotY1);
      rect(x-barWidth/2, y, x+barWidth/2, plotY2);
    }
  }
}

Here, the barWidth variable makes the bars four pixels wide. Calculating widths for a bar chart can be done with algebra (by dividing the distance between plotX2 and plotX1 by the number of rows of data) or by trial and error.

It’s also necessary to disable the lines drawn in drawYearLabels( ) because vertical grid lines will conflict with the bars.

Unfortunately, this is too much data to show at this width, resulting in the vibrating texture shown in Figure 4-14, which looks more like a swatch of patterned fabric.

Figure 4-14. Overly busy bar chart

This example highlights an important consideration: when deciding on a representation, use a bar chart only when there’s enough room to leave clear gaps between bars.

Once a bar chart is laid out properly, the method of using white grid lines in Figure 4-13 could be better utilized to highlight the divisions on the left axis by erasing thin horizontal lines across the plot. Like the version that sliced the area plot into individual decades, this would provide another cue to help the viewer quickly read data values.

Text Labels As Tabbed Panes (Interact)

Using keys to navigate an interface should be used only during testing. A more sophisticated method is to use on-screen buttons, as users expect from a modern interface. This section describes how to replace the drawTitle( ) function with drawTitleTabs( ) to introduce a series of tabbed panel—one for each data series.

Adding the Necessary Variables

The tabTop and tabBottom variables specify the upper and lower edge of the tabs. The tabLeft and tabRight variables store the coordinates for the left and right edges of each tab so that we can detect mouse clicks inside the tabs. The tabPad variable specifies the amount of padding on the left and right of the tab text:

float[] tabLeft, tabRight; // Add above setup(  )
float tabTop, tabBottom;
float tabPad = 10;

Drawing Tabs Instead of a Single Title

The important part of this method keeps track of a value named runningX to calculate the positions of each tab. The width of each tab is calculated using textWidth( ), and the tabPad value is added to provide padding on the sides:

void drawTitleTabs(  ) {
  rectMode(CORNERS);
  noStroke(  );
  textSize(20);
  textAlign(LEFT);

  // On first use of this method, allocate space for an array
  // to store the values for the left and right edges of the tabs.
  if (tabLeft == null) {
    tabLeft = new float[columnCount];
    tabRight = new float[columnCount];
  }

  float runningX = plotX1;
  tabTop = plotY1 - textAscent(  ) - 15;
  tabBottom = plotY1;

  for (int col = 0; col < columnCount; col++) {
    String title = data.getColumnName(col);
    tabLeft[col] = runningX;
    float titleWidth = textWidth(title);
    tabRight[col] = tabLeft[col] + tabPad + titleWidth + tabPad;

    // If the current tab, set its background white; otherwise use pale gray.
    fill(col == currentColumn ? 255 : 224);
    rect(tabLeft[col], tabTop, tabRight[col], tabBottom);

    // If the current tab, use black for the text; otherwise use dark gray.
    fill(col == currentColumn ? 0 : 64);
    text(title, runningX + tabPad, plotY1 − 10);

    runningX = tabRight[col];
  }
}

This piece of code also introduces the conditional operator, identified by the ?. The conditional statement:

fill(col == currentColumn ? 0 : 64);

is equivalent to writing:

if (col == currentColumn) {
  fill(0);
} else {
  fill(64);
}

The benefit of the former is compact code: a single line instead of five. The conditional operator is most useful in situations such as this one, where a simple if test is used to control something straightforward like the fill color. In this case, it can be argued that the shorter code is more readable than all five lines. However, use the conditional operator sparingly because overuse can result in code that is difficult to read.

Handling Mouse Input

Next, we’ll add the mousePressed( ) method, which tests whether the mouse is inside one tab or another. This method is a simple matter of iterating through each tab and checking the mouseX and mouseY coordinates against the variables that contain the boundaries of each tab rectangle. If the mouseY value is in the correct range, mouseX is tested against each tabLeft and tabRight value. If inside, the value of currentColumn is updated with the setColumn( ) method:

void mousePressed(  ) {
  if (mouseY > tabTop && mouseY < tabBottom) {
    for (int col = 0; col < columnCount; col++) {
      if (mouseX > tabLeft[col] && mouseX < tabRight[col]) {
        setColumn(col);
      }
    }
  }
}

void setColumn(int col) {
  if (col != currentColumn) {
    currentColumn = col;
  }
}

The setColumn( ) method is expressed in a separate piece of code because it will be modified in the next section, and the keyPressed( ) method should simply be removed.

Finally, the result is shown in Figure 4-15.

Figure 4-15. Clickable tabs

Better Tab Images (Refine)

The tabs in Figure 4-15 look pretty boring, but some tweaking of the text, the colors, and a line here and there could improve them. Another option is to load the tabs from a series of image files. Three separate image files would be used for the nonselected state of the tabs, and three others would be used for the selected state. Then, instead of setting the fill differently for the rectangle and the text title, one of the six images would be used in its place. A modified version of the code looks like this:

float[] tabLeft, tabRight; // Add above setup(  )
float tabTop, tabBottom;
float tabPad = 10;PImage[] tabImageNormal;
PImage[] tabImageHighlight;

void drawTitleTabs(  ) {
  rectMode(CORNERS);
  noStroke(  );
  textSize(20);
  textAlign(LEFT);

  // Allocate the tab position array, and load the tab images.
  if (tabLeft == null) {
    tabLeft = new float[columnCount];
    tabRight = new float[columnCount];

    tabImageNormal = new PImage[columnCount];
    tabImageHighlight = new PImage[columnCount];
    for (int col = 0; col < columnCount; col++) {
      String title = data.getColumnName(col);
      tabImageNormal[col] = loadImage(title + "-unselected.png");
      tabImageHighlight[col] = loadImage(title + "-selected.png");
    }
  }

  float runningX = plotX1;
  tabBottom = plotY1;
  // Size based on the height of the tabs by checking the
  // height of the first (all images are the same height)
  tabTop = plotY1 - tabImageNormal[0].height;

  for (int col = 0; col < columnCount; col++) {
    String title = data.getColumnName(col);
    tabLeft[col] = runningX;
    float titleWidth = tabImageNormal[col].width;
    tabRight[col] = tabLeft[col] + tabPad + titleWidth + tabPad;

    PImage tabImage = (col == currentColumn) ?
      tabImageHighlight[col] : tabImageNormal[col];
    image(tabImage, tabLeft[col], tabTop);

    runningX = tabRight[col];
  }
}

When preparing the images, be sure to keep their heights the same. As with the text version, the widths of the titles can vary, but the width of the selected versus non-selected version should always be the same. The images should be named based on the title of each column, so, in this case, the following six files are used:

Milk-selected.png
Tea-selected.png
Coffee-selected.png
Milk-unselected.png
Tea-unselected.png
Coffee-unselected.png

For those who want to use standard interface components instead of making their own, later chapters cover integrating Processing with Java code. Custom components are useful when a unique interface is preferred, but they are less helpful if a standard interface is more appropriate for your audience.

Interpolation Between Data Sets (Interact)

Chapter 3 showed how to interpolate between values in a data set with the use of the Integrator class. Download itfrom http://benfry.com/writing/series/Integrator.pde.

The changes are identical to those in the previous chapter. First, declare the array of Integrator objects before setup( ):

Integrator[] interpolators;

Inside setup( ), create each Integrator and set its initial value:

  interpolators = new Integrator[rowCount];
  for (int row = 0; row < rowCount; row++) {
    float initialValue = data.getFloat(row, 0);
    interpolators[row] = new Integrator(initialValue);
    interpolators[row].attraction = 0.1; // Set lower than the default
  }

The attraction value is set to 0.1 (instead of the default, 0.2) so that the interpolation occurs at a less frantic pace.

In draw( ), each Integrator is updated:

   for (int row = 0; row < rowCount; row++) {
    interpolators[row].update(  );
  }

Next, for whatever variation of the drawData( ) function you would like to use, replace its data.getFloat( ) line. The original looks like this:

float value = data.getFloat(row, col);

Change the line to the following to use the interpolated values:

float value = interpolators[row].value;

Finally, modify setColumn( ) to set each Integrator to target the value for the current column:

void setColumn(int col) {
  currentColumn = col;

  for (int row = 0; row < rowCount; row++) {
    interpolators[row].target(data.getFloat(row, col));
  }
}

The final code, with modifications highlighted, follows:

FloatTable data;
float dataMin, dataMax;

float plotX1, plotY1;
float plotX2, plotY2;
float labelX, labelY;

int rowCount;
int columnCount;
int currentColumn = 0;

int yearMin, yearMax;
int[] years;

int yearInterval = 10;
int volumeInterval = 10;
int volumeIntervalMinor = 5;

float[] tabLeft, tabRight;
float tabTop, tabBottom;
float tabPad = 10;Integrator[] interpolators;

PFont plotFont;


void setup(  ) {
  size(720, 405);
  data = new FloatTable("milk-tea-coffee.tsv");
  rowCount = data.getRowCount(  );
  columnCount = data.getColumnCount(  );

  years = int(data.getRowNames(  ));
  yearMin = years[0];
  yearMax = years[years.length - 1];

  dataMin = 0;
  dataMax = ceil(data.getTableMax(  ) / volumeInterval) * volumeInterval;

  interpolators = new Integrator[rowCount];
  for (int row = 0; row < rowCount; row++) {
    float initialValue = data.getFloat(row, 0);
    interpolators[row] = new Integrator(initialValue);
    interpolators[row].attraction = 0.1; // Set lower than the default
  }

  plotX1 = 120;
  plotX2 = width - 80;
  labelX = 50;
  plotY1 = 60;
  plotY2 = height - 70;
  labelY = height - 25;

  plotFont = createFont("SansSerif", 20);
  textFont(plotFont);

  smooth(  );
}


void draw(  ) {
  background(224);

  // Show the plot area as a white box
  fill(255);
  rectMode(CORNERS);
  noStroke(  );
  rect(plotX1, plotY1, plotX2, plotY2);

  drawTitleTabs(  );
  drawAxisLabels(  );

  for (int row = 0; row < rowCount; row++) {
    interpolators[row].update(  );
  }

  drawYearLabels(  );
  drawVolumeLabels(  );

  noStroke(  );
  fill(#5679C1);
  drawDataArea(currentColumn);
}
void drawTitleTabs(  ) {
  rectMode(CORNERS);
  noStroke(  );
  textSize(20);
  textAlign(LEFT);

  // On first use of this method, allocate space for an array
  // to store the values for the left and right edges of the tabs.
  if (tabLeft == null) {
    tabLeft = new float[columnCount];
    tabRight = new float[columnCount];
  }

  float runningX = plotX1;
  tabTop = plotY1 - textAscent(  ) - 15;
  tabBottom = plotY1;

  for (int col = 0; col < columnCount; col++) {
    String title = data.getColumnName(col);
    tabLeft[col] = runningX;
    float titleWidth = textWidth(title);
    tabRight[col] = tabLeft[col] + tabPad + titleWidth + tabPad;

    // If the current tab, set its background white; otherwise use pale gray.
    fill(col == currentColumn ? 255 : 224);
    rect(tabLeft[col], tabTop, tabRight[col], tabBottom);

    // If the current tab, use black for the text; otherwise use dark gray.
    fill(col == currentColumn ? 0 : 64);
    text(title, runningX + tabPad, plotY1 - 10);

    runningX = tabRight[col];
  }
}


void mousePressed(  ) {
  if (mouseY > tabTop && mouseY < tabBottom) {
    for (int col = 0; col < columnCount; col++) {
      if (mouseX > tabLeft[col] && mouseX < tabRight[col]) {
        setColumn(col);
      }
    }
  }
}


void setCurrent(int col) {
  currentColumn = col;

  for (int row = 0; row < rowCount; row++) {
    interpolators[row].target(data.getFloat(row, col));
  }
}
void drawAxisLabels(  ) {
  fill(0);
  textSize(13);
  textLeading(15);

  textAlign(CENTER, CENTER);
  text("Gallons\nconsumed\nper capita", labelX, (plotY1+plotY2)/2);
  textAlign(CENTER);
  text("Year", (plotX1+plotX2)/2, labelY);
}


void drawYearLabels(  ) {
  fill(0);
  textSize(10);
  textAlign(CENTER);

  // Use thin, gray lines to draw the grid
  stroke(224);
  strokeWeight(1);

  for (int row = 0; row < rowCount; row++) {
    if (years[row] % yearInterval == 0) {
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      text(years[row], x, plotY2 + textAscent(  ) + 10);
      line(x, plotY1, x, plotY2);
    }
  }
}


void drawVolumeLabels(  ) {
  fill(0);
  textSize(10);
  textAlign(RIGHT);

  stroke(128);
  strokeWeight(1);

  for (float v = dataMin; v <= dataMax; v += volumeIntervalMinor) {
    float y = map(v, dataMin, dataMax, plotY2, plotY1);
    if (v % volumeInterval == 0) { // If a major tick mark
      float textOffset = textAscent(  )/2; // Center vertically
      if (v == dataMin) {
        textOffset = 0; // Align by the bottom
      } else if (v == dataMax) {
        textOffset = textAscent(  ); // Align by the top
      }
      text(floor(v), plotX1 - 10, y + textOffset);
      line(plotX1 - 4, y, plotX1, y); // Draw major tick
    } else {
      //line(plotX1 - 2, y, plotX1, y); // Draw minor tick
    }
  }
 }


void drawDataArea(int col) {
  beginShape(  );
  for (int row = 0; row < rowCount; row++) {
    if (data.isValid(row, col)) {
      float value = interpolators[row].value;
      float x = map(years[row], yearMin, yearMax, plotX1, plotX2);
      float y = map(value, dataMin, dataMax, plotY2, plotY1);
      vertex(x, y);
    }
  }
  vertex(plotX2, plotY2);
  vertex(plotX1, plotY2);
  endShape(CLOSE);
}

End of the Series

In this chapter, we looked at the most common form of data plot: the time series. The point was to get comfortable with functions such as map( ), pick up some principles on how to choose a representation, and see how a few lines of code can help produce an alternate representation or a more refined appearance. The techniques implemented here are useful for nearly any type of plot, as the algebra for placement and considerations for use will be identical across all other data sets that we examine.

Developers familiar with Processing or Java might want to make this code into a class. Classes are a useful means for encapsulating data sets. For instance, this code could be made into a class named TimeSeries to handle arbitrary data stored in a table. This might be a useful abstraction, but keep in mind how you customize the code once it’s in a class. The final version of the program listing in this chapter is just over 200 lines (a little more than three printed pages). Once you’ve moved this code into a 200-line class, how do you keep it flexible? Do you modify it directly or subclass it? Is it necessary to create a new subclass for each new type of representation, when each new representation is between 5 and 20 lines apiece? Always weigh such decisions in terms of how the code will be used. If only one representation is required for your particular project, why bother maintaining multiple subclasses? Just do the representation right the first time. And when reusing the code in your next project, you’ll probably change at least 10% of the base code anyway, so there’s no need to maintain several subclasses. As our projects become more complicated, we’ll do more to encapsulate code into modular units, while doing our best to avoid needless levels of abstraction.

Of course, there are libraries that allow you to plot data in a number of ways, particularly for simple things such as time series or bar charts. For Java coders, JFreeChart is a widely used example (see http://www.jfree.org/jfreechart). JFreeChart is a nice tool for basic charting and graphing, but it doesn’t allow the kind of flexible customization taught here—which you are hopefully coming to appreciate. This book intends to teach you the starting point for drawing basic representations, such as a plot or chart, and then goes on to show how they can be manipulated in a more sophisticated manner than can be done with standard tools.

^[2]^* Tufte, Edward R. The Visual Display of Quantitative Information. Cheshire, Conn.: Graphics Press, 1983.

Get Visualizing Data now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial

Visualizing Data by Ben Fry