VLSI Digital Signal Processing Systems: Design and Implementation

5.7    PROBLEMS

1. Unfold the DFG in Fig. 5.20 using unfolding factors 3 and 4.
2. Unfold the DFGs in Fig. 5.21 using unfolding factors 2 and 5.
3. Prove the relationship in (5.3) used to show that unfolding preserves the number of delays.
4. This problem attempts to show that a complex loop, which is a combination of 2 simple or fundamental loops, cannot introduce a new iteration bound. To show this, consider two loops with loop computation times T₁ and T₂, respectively, and with number of delay elements N₁ and N₂, respectively. Let T₁/N₁ > T₂/N₂ hold. Show that

   

5. Our objective in this problem is to prove that the critical path of a J-unfolded DFG is a monotonically nondecreasing function with respect to J [11]. To show this, prove that the critical path of a J-unfolded DFG is greater than or equal to the critical path of the (J − l)-unfolded DFG.
6. Prove that the following iterative algorithm computes the minimum unfolding factor for a nonrecursive DFG such that the iteration period of T is achievable. It is assumed that pipelining and/or retiming are not used to reduce the critical path.

   Repeat until T_crit ≤ JT

   {

   

   

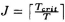
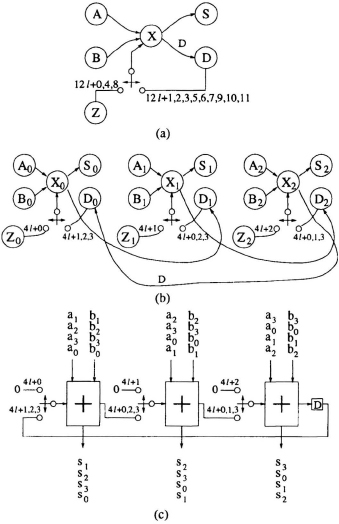
   Fig 5.19    (a) The DFG in Fig. 5.16 redrawn so it is compatible with the unfolding ...