VLSI Digital Signal Processing Systems: Design and Implementation

9.6    PROBLEMS

1. Express the 2-parallel filter algorithm:

   

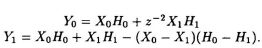
   in terms of a postprocessing matrix, a diagonal matrix, and a preprocessing matrix. Obtain another 2-parallel structure using the transpose of this formulation.

2. Consider a 6-tap FIR filter with unit-sample response

   

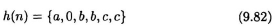
   and

   

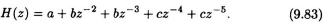
   The sequential filter has 3 distinct coefficients and can be implemented using 3 multiplication operations as shown in Fig. 9.35. The 2-parallel filter will not require more than 6 multiplication operations. Design the structure of a 2-parallel implementation of this filter. Show the coefficients of all multipliers in your structure.

3. Design a 3-parallel filter structure using the transpose of the 3-parallel filter algorithm presented in Section 9.2.2.1.
4. Using the following 3-parallel linear convolution:

   

   

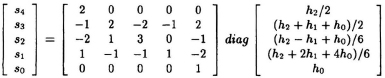
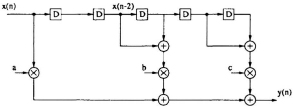
   Fig. 9.35    Figure for Problem 2.

   

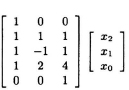
   obtain a 3-parallel filter that requires 5 subfiltering operations.

5. Use ...