4.4. Drawing a Rounded Rectangle

Problem

You want to draw a rectangle with rounded corners, an offset, or rotation.

Solution

Create a custom MovieClip.drawRectangle( ) method using

the Drawing API and invoke it on a movie clip.

Discussion

The drawSimpleRectangle( ) method from Recipe 4.3 is, as the name suggests, quite simple.

Let’s create a more complex version that also:

Draws a rectangle with a specified angle of rotation
Let’s you specify the rectangle center’s coordinates
Can draw a rectangle with rounded corners

The drawRectangle( ) method accepts six parameters:

width: The width of the rectangle in pixels
height: The height of the rectangle in pixels
round: The radius (in pixels) of the arc that is used to round the corners. If the value is undefined or 0, the corners remain square.
rotation: The clockwise rotation to apply to the rectangle in degrees. If undefined, the rectangle is not rotated.
x: The x coordinate of the center point for the rectangle. If undefined, the rectangle is centered at x = 0.
y: The y coordinate of the center point for the rectangle. If undefined, the rectangle is centered at y = 0.

Here is our enhanced drawRectangle( ) method, defined on MovieClip.prototype, so it’s available to all movie clip instances:

// Include the custom Math library from Chapter 5 to access Math.degToRad(  ).
#include "Math.as"

MovieClip.prototype.drawRectangle = function (width, height, round, rotation, x, y) {
  // Make sure the rectangle is at least as wide and tall as the rounded corners.
  if (width < (round * 2)) {
    width = round * 2;
  }
  if (height < (round * 2)) {
    height = round * 2;
  }

  // Convert the rotation from degrees to radians.
  rotation = Math.degToRad(rotation);

  // Calculate the distance from the rectangle's center to one of the corners (or
  // where the corner would be in rounded-cornered rectangles). See the line labeled
  // r in Figure 4-2.
  var r = Math.sqrt(Math.pow(width/2, 2) + Math.pow(height/2, 2));

  // Calculate the distance from the rectangle's center to the upper edge of the
  // bottom-right rounded corner. See the line labeled rx in Figure 4-2. When round
  // is 0, rx is equal to r.
  var rx = Math.sqrt(Math.pow(width/2, 2) + Math.pow((height/2) - round, 2));

  // Calculate the distance from the rectangle's center to the lower edge of the
  // bottom-right rounded corner. See the line labeled ry in Figure 4-2. When round
  // is 0, ry is equal to r.
  var ry = Math.sqrt(Math.pow((width/2) - round, 2) + Math.pow(height/2, 2));

  // Calculate angles. r1Angle is the angle between the X axis that runs through the
  // center of the rectangle and the line rx. r2Angle is the angle between rx and r.
  // r3Angle is the angle between r and ry. And r4Angle is the angle between ry and
  // the Y axis that runs through the center of the rectangle.
  var r1Angle = Math.atan( ((height/2) - round) /( width/2) );
  var r2Angle = Math.atan( (height/2) / (width/2) ) - r1Angle;
  var r4Angle = Math.atan( ((width/2) - round) / (height/2) );
  var r3Angle = (Math.PI/2) - r1Angle - r2Angle - r4Angle;

  // Calculate the distance of the control point from the 
  // arc center for the rounded corners.
  var ctrlDist = Math.sqrt(2 * Math.pow(round, 2));

  // Declare the local variables used to calculate the control point.
  var ctrlX, ctrlY;

  // Calculate where to begin drawing the first side segment and then draw it.
  rotation += r1Angle + r2Angle + r3Angle;
  var x1 = x + ry * Math.cos(rotation);
  var y1 = y + ry * Math.sin(rotation);
  this.moveTo(x1, y1);
  rotation += 2 * r4Angle;
  x1 = x + ry * Math.cos(rotation);
  y1 = y + ry * Math.sin(rotation);
  this.lineTo(x1, y1);

  // Set rotation to the starting point for the next side segment and calculate the x
  // and y coordinates.
  rotation += r3Angle + r2Angle;
  x1 = x + rx * Math.cos(rotation);
  y1 = y + rx * Math.sin(rotation);

  // If the corners are rounded, calculate the control point for the corner's curve
  // and draw it.
  if (round > 0) {
    ctrlX = x + r * Math.cos(rotation - r2Angle);
    ctrlY = y + r * Math.sin(rotation - r2Angle);
    this.curveTo(ctrlX, ctrlY, x1, y1);
  }

  // Calculate the end point of the second side segment and draw the line.
  rotation += 2 * r1Angle;
  x1 = x + rx * Math.cos(rotation);
  y1 = y + rx * Math.sin(rotation);
  this.lineTo(x1, y1);

  // Calculate the next line segment's starting point.
  rotation += r2Angle + r3Angle;
  x1 = x + ry * Math.cos(rotation);
  y1 = y + ry * Math.sin(rotation);

  // Draw the rounded corner, if applicable.
  if (round > 0) {
    ctrlX = x + r * Math.cos(rotation - r3Angle);
    ctrlY = y + r * Math.sin(rotation - r3Angle);
    this.curveTo(ctrlX, ctrlY, x1, y1);
  }

  // Calculate the end point of the third segment and draw the line.
  rotation += 2 * r4Angle;
  x1 = x + ry * Math.cos(rotation);
  y1 = y + ry * Math.sin(rotation);
  this.lineTo(x1, y1);

  // Calculate the starting point of the next segment.
  rotation += r3Angle + r2Angle;
  x1 = x + rx * Math.cos(rotation);
  y1 = y + rx * Math.sin(rotation);

  // If applicable, draw the rounded corner.
  if (round > 0) {
    ctrlX = x + r * Math.cos(rotation - r2Angle);
    ctrlY = y + r * Math.sin(rotation - r2Angle);
    this.curveTo(ctrlX, ctrlY, x1, y1);
  }

  // Calculate the end point for the fourth segment and draw it.
  rotation += 2 * r1Angle;
  x1 = x + rx * Math.cos(rotation);
  y1 = y + rx * Math.sin(rotation);
  this.lineTo(x1, y1);

  // Calculate the end point for the next corner arc and, if applicable, draw it.
  rotation += r3Angle + r2Angle;
  x1 = x + ry * Math.cos(rotation);
  y1 = y + ry * Math.sin(rotation);
  if (round > 0) {
    ctrlX = x + r * Math.cos(rotation - r3Angle);
    ctrlY = y + r * Math.sin(rotation - r3Angle);
    this.curveTo(ctrlX, ctrlY, x1, y1);
  }
}

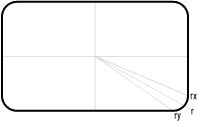
Figure 4-2 shows the geometry when drawing the rounded corners for the rectangle.

Figure 4-2. A conceptual illustration of drawing a rounded rectangle

The preceding example will be clearer with a closer examination.

The ActionScript trigonometric methods require angles measured in radians. Therefore, whenever you specify an angle in degrees (which is generally easier for humans), you must convert the units to radians before passing them to ActionScript’s trigonometric methods. In this case, we convert the rotation parameter from degrees to radians using the Math.degToRad( ) method from Recipe 5.12:

rotation = Math.degToRad(rotation);

The length of the three imaginary lines used for drawing the rounded corners, as shown in Figure 4-2, are calculated using the Pythagorean theorem, as discussed in Recipe 5.13. In our example, these distances are:

var r  = Math.sqrt(Math.pow(width/2, 2) + Math.pow(height/2, 2));
var rx = Math.sqrt(Math.pow(width/2, 2) + Math.pow((height/2) - round, 2));
var ry = Math.sqrt(Math.pow((width/2) - round, 2) + Math.pow(height/2, 2));

Next, we must calculate the angles formed between the axes and the lines r, rx, and ry. These angles are used to determine the x and y coordinates of the starting and ending side segments. If you know the lengths of the sides of a right triangle, you can determine the angles that they form. Because the axes and the lines r, rx, and ry can be formed into right triangles you can determine the angles these lines form using the tangent and arctangent. The tangent in a right triangle is defined as the ratio of the side opposite the angle to the side adjacent to the angle. The arctangent is the inverse of the tangent function, so we use the following to determine the angles:

var r1Angle = Math.atan(((height/2) - round)/(width/2));
var r2Angle = Math.atan((height/2)/(width/2)) - r1Angle;
var r4Angle = Math.atan(((width/2) - round)/(height/2));
var r3Angle = (Math.PI/2) - r1Angle - r2Angle - r4Angle;

The corners are each composed of a single curve that is a semicircle. To determine the distance between the semicircle’s center point and the control point used to draw that curve, again use the Pythagorean theorem:

var ctrlDist = Math.sqrt(2 * Math.pow(round, 2));

The first thing you want to do when you draw the rectangle is to move the imaginary pen to a starting point on the rectangle without actually drawing a line. In this example, the calculated starting point is at the right end of the bottom segment (of an unrotated rectangle). If you know the distance between two points and the angle (the opposite angle formed by an imaginary right triangle with the known line being the hypotenuse), you can calculate the x and y coordinates of the destination point using trigonometric functions. The x coordinate is determined by the distance times the cosine of the angle. The y coordinate is determined by the distance times the sine of the angle. In this example the x and y coordinates (x1 and y1) are also offset by the x and y parameters to draw a rectangle whose center is not at (0, 0):

rotation += r1Angle + r2Angle + r3Angle;
var x1 = x + ry * Math.cos(rotation);
var y1 = y + ry * Math.sin(rotation);
this.moveTo(x1, y1);

The remainder of the example follows the same pattern: draw a line, draw a rounded corner (if applicable), and then move to the next side segment. The new coordinates for each segment are calculated using the same process as described previously. Once you have defined and included the drawRectangle( ) method in your Flash document, you can quickly draw a rectangle within any movie clip instance. Don’t forget that you still need to define the line style (see Recipe 4.1) before Flash will actually draw anything.

// Create a new movie clip into which to draw the rectangle.
this.createEmptyMovieClip("rectangle_mc", 1);

// Define a 1-pixel, black, solid line style.
rectangle_mc.lineStyle(1, 0x000000, 100);

// Draw a rectangle with dimensions of 100   ×   200. The rectangle has rounded corners
// with radii of 10, and it is rotated 45 degrees clockwise.
rectangle_mc.drawRectangle(100, 200, 10, 45);

You can draw a square by using the drawRectangle( ) method with equal height and width values:

this.createEmptyMovieClip("square_mc", 1);
square_mc.lineStyle(1, 0x000000, 100);
square_mc.drawRectangle(100, 100);

You can draw filled rectangles by invoking beginFill( ) or beginGradientFill( ) before drawRectangle( ) and invoking endFill( ) after drawRectangle( ):

this.createEmptyMovieClip("filledRectangle_mc", 1);
filledRectangle_mc.lineStyle(1, 0x000000, 100);   // Define a black, 1-pixel border.
filledRectangle_mc.beginFill(0x0000FF);           // Define a solid blue fill.
filledRectangle_mc.drawRectangle(100, 200);
filledRectangle_mc.endFill(  );

Actionscript Cookbook by Joey Lott

4.4. Drawing a Rounded Rectangle

Problem

Solution

Discussion

See Also

Don’t leave empty-handed

It’s yours, free.

Check it out now on O’Reilly