Data Structures and Algorithms in Python

Appendix B

Useful Mathematical Facts

In this appendix we give several useful mathematical facts. We begin with some combinatorial definitions and facts.

Logarithms and Exponents

The logarithm function is defined as

The following identities hold for logarithms and exponents:

1. log_b ac = log_ba + log_bc
2. log_b a/c = log_ba − log_bc
3. log_b a^c = clog_ba
4. log^b a = (log_ca)/log_cb
5. b^{log_c a} = a^log_cb
6. (b^a)^c = b^ac
7. b^a b^c = b^a+c
8. b^a /b^c = b^a−c

In addition, we have the following:

Proposition B.1: If a > 0, b > 0, and c > a + b, then

loga + logb < 2logc − 2.

Justification: It is enough to show that ab < c²/4. We can write

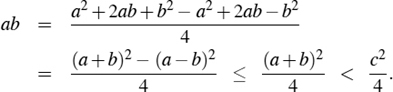
The natural logarithm function lnx = log_e x, where e = 2.71828. . ., is the value of the following progression:

In addition,

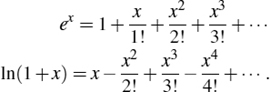
There are a number of useful inequalities relating to these functions (which derive from these definitions).

Proposition B.2: If x > −1,

Proposition B.3: For 0 ≤ x < 1,

Proposition B.4: For any two positive real numbers x and n,

Integer Functions and Relations

The “floor” ...