Digital Communication Systems

APPENDIX

B  Bounds on the Q-Function

Following Chapter 3, we define the Q-function as

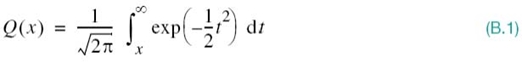
which represents the area under the tail of the standard Gaussian distribution. In this appendix, we derive some useful bounds on the Q-function for large positive values of x.

To this end, we change the variable of integration in (B.1) by setting

and then recast (B.1) in the form

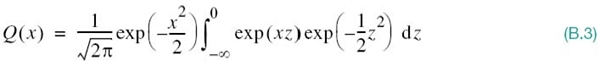
For any real z, the value of exp (−1/2z²) lies between the successive partial sums of the power series:

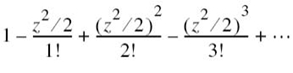
Therefore, for x > 0 we find that, on using (n + 1) terms of this series, the Q-function lies between the values taken by the integral

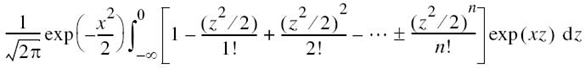
for even n and odd n. We now make another change in the integration variable by setting

and also use the definite integral

Doing so, we obtain the following asymptotic expansion for the ...