Machine Learning for Email

Chapter 4. Ranking: Priority Inbox

How Do You Sort Something When You Don’t Know the Order?

In Chapter 3, we discussed in detail the concept of binary classification—that is, placing items into one of two types or classes. In many cases, we will be satisfied with an approach that can make such a distinction. But what if the items in one class are not created equally, and we want to rank the items within a class? In short, what if we want to say that one email is the most spammy, while another is the second, or we want to distinguish among them in some other meaningful way? Suppose we not only wanted to filter spam from our email, but we also wanted to place “more important” messages at the top of the queue. This is a very common problem in machine learning, and it will be the focus of this chapter.

Generating rules for ranking a list of items is an increasingly common task in machine learning, yet you may not have thought of it in these terms. More likely, you have heard of something like a recommendation system, which implicitly produces a ranking of products. Even if you have not heard of a recommendation system, it’s almost certain that you have used or interacted with a recommendation system at some point. Some of the most successful e-commerce websites have benefitted from leveraging data on their users to generate recommendations for other products their users might be interested in.

For example, if you have ever shopped at Amazon.com, then you have interacted with a recommendation system. The problem Amazon faces is simple: what items in their inventory are you most likely to buy? The implication of that statement is that the items in Amazon’s inventory have an ordering specific to each user. Likewise, Netflix.com has a massive library of DVDs available to its customers to rent. In order for those customers to get the most out of the site, Netflix employs a sophisticated recommendation system to present people with rental suggestions.

For both companies, these recommendations are based on two kinds of data. First, there is the data pertaining to the inventory itself. For Amazon, if the product is a television, this data might contain the type (i.e., plasma, LCD, LED), manufacturer, price, and so on. For Netflix, this data might be the genre of a film, its cast, director, running time, etc. Second, there is the data related to the browsing and purchasing behavior of the customers. This sort of data can help Amazon understand what accessories most people look for when shopping for a new plasma TV and can help Netflix understand which romantic comedies George A. Romero fans most often rent. For both types of data, the features are well identified. That is, we know the labels for categorical data like product type or movie genre; likewise, user-generated data is well structured in the form of purchase/rental records and explicit ratings.

Because we usually have explicit examples of the outputs of interest when doing ranking, this is a type of machine learning problem that is often called supervised learning. This is in contrast to unsupervised learning, where there are no pre-existing examples of the outputs when we start working with the data. To better understand the difference, think of supervised learning as a process of learning through instruction. For example, if you want to teach someone how to bake a cherry pie, you might hand them a recipe and then let them taste the pie that results. After seeing how the result tastes, they might decide to adjust the ingredients a bit. Having a record of the ingredients they’ve used (i.e., the inputs) and the taste of the result (i.e., the output) means that they can analyze the contributions of each ingredient and try to find the perfect cherry pie recipe.

Alternatively, if you only knew that dishes with refried beans tend to also come with tortillas, while dishes with baked cherries tend to come with dough, you might be able to group other ingredients into classes that would ultimately resemble the sorts of things you’d use to make Mexican food versus the sorts of things you’d use to make American desserts. Indeed, a common form of unsupervised learning is clustering, where we want to assign items to a fixed number of groups based on commonalities or differences.

If you have already read and worked through the exercise in Chapter 3, then you have already solved a supervised learning problem. For spam classification, we knew the terms associated with spam and ham messages, and we trained our classifier using that recipe. That was a very simple problem, and so we were able to obtain relatively good classification results using a feature set with only a single element: email message terms. For ranking, however, we need to assign a unique weight to each item to stratify them in a finer way.

So in the next section we will begin to address the question proposed in the title of this section: how do you sort something when you don’t already know its order? As you may have guessed, to do this in the context of ordering emails by their importance, we will have to reword the question in terms of the features available to us in the email data and how those features relate to an email’s priority.

Ordering Email Messages by Priority

What makes an email important? To begin to answer this, let’s first step back and think about what email is. First, it is a transaction-based medium. People send and receive messages over time. As such, in order to determine the importance of an email, we need to focus on the transactions themselves. Unlike the spam classification task, where we could use static information from all emails to determine their type, to rank emails by importance we must focus on the dynamics of the in- and out-bound transactions. Specifically, we want to make a determination as to the likelihood a person will interact with a new email once it has been received. Put differently, given the set of features we have chosen to study, how likely is the reader to perform an action on this email in the immediate future?

The critical new dimension that this problem incorporates is time. In a transaction-based context, in order to rank things by importance, we need to have some concept of time. A natural way to use time to determine the importance of an email is to measure how long it takes a user to perform some action on an email. The shorter the average time it takes a user to perform some action on an email, given its set of features, the more important emails of that type may be.

The implicit assumption in this model is that more important emails will be acted on sooner than less important emails. Intuitively this makes sense. All of us have stared at the queue in our inbox and filtered through emails that needed immediate response versus those that could wait. The filtering that we do naturally is what we will attempt to teach our algorithm to do in the following sections. Before we can begin, however, we must determine which features in email messages are good proxy measures for priority.

Priority Features Email

If you use Google’s Gmail service for your email, you will know that the idea of a “priority inbox” was first popularized by Google in 2010. Of course, it was this problem that inspired the case study on ranking for this chapter, so it will be useful to revisit the approach that Google took in implementing their ranking algorithm as we move toward designing our own. Fortunately, several months after the priority inbox feature was released by Google, they published a paper, entitled “The Learning Behind Gmail Priority Inbox,” which describes their strategy for designing the supervised learning approach and how to implement it at scale DA10. For the purposes of this chapter, we are only interested in the former, but we highly recommend the paper as a supplement to what we discuss here. And at four pages in length, it is well worth the time commitment.

As we mentioned, measuring time is critical, and in Google’s case they have the luxury of a long and detailed history of users’ interactions with email. Specifically, Google’s priority inbox attempts to predict the probability that a user will perform some action on an email within a fixed number of seconds from its delivery. The set of actions a user can perform in Gmail is large: reading, replying, labeling, etc. Also, delivery is not explicitly the time at which an email is received by the server, but the time at which it is delivered to the user—i.e., when they check their email.

As with spam classification, this is a relatively simple problem to state: what is the probability that a user will perform some actions, within our set of possible actions, between some minimum and maximum numbers of seconds, given a set of features for that email and the knowledge that the user has recently checked their email?

Within the universe of possible email features, which did Google decide to focus on? As you might expect, they incorporated a very large number of features. As the authors of the paper note, unlike spam classification—which nearly all users will code the same way—everyone has a different way of ordering the priority of email. Given this variability in how users may evaluate the feature set, Google’s approach needed to incorporate multiple features. To begin designing the algorithm, Google engineers explored various different types of email features, which they describe as follows:

There are many hundred features falling into a few categories. Social features are based on the degree of interaction between sender and recipient, e.g., the percentage of a sender’s mail that is read by the recipient. Content features attempt to identify headers and recent terms that are highly correlated with the recipient acting (or not) on the mail, e.g., the presence of a recent term in the subject. Recent user terms are discovered as a pre-processing step prior to learning. Thread features note the user’s interaction with the thread so far, e.g., if a user began a thread. Label features examine the labels that the user applies to mail using filters. We calculate feature values during ranking and we temporarily store those values for later learning. Continuous features are automatically partitioned into binary features using a simple ID3 style algorithm on the histogram of the feature values.

As we mentioned, Google has a long history of its users’ interactions with Gmail, which affords them a rich perspective into what actions users perform on emails and when. Unfortunately, such detailed email logs are not available to us in this exercise. Instead, we will again be using the SpamAssassin Public Corpus, available for free download at: http://spamassassin.apache.org/publiccorpus/.

Though this data set was distributed as a means of testing spam classification algorithms, it also contains a convenient timeline of a single user’s email. Given this single thread, we can repurpose the data set to design and test a priority email ranking system. Also, we will only focus on the ham emails from this data set, so we know that all of the messages we will examine are those that the user would want in their inbox.

Before we can proceed, however, we must consider how our data differs from that of a full-detail email log—such as Google’s—and how that affects the features we will be able to use in our algorithm. Let’s begin by going through each of the four categories proposed by Google and determining how they might fit into the data we are using.

Warning

The most critical difference between a full-detail email log and what we will be working with is that we can only see the messages received. This means that we will be effectively “flying half-blind,” as we have no data on when and how a user responded to emails, or if the user was the originator of a thread. This is a significant limitation, and therefore the methods and algorithms used in this chapter should be considered as exercises only, and not examples of how enterprise priority inbox systems should be implemented. What we hope to accomplish is to show how, even with this limitation, we can use the data we have to create proxy measures for email importance and still design a relatively good ranking system.

Given that email is a transaction-based medium, it follows that social features will be paramount in assessing the importance of an email. In our case, however, we can only see half of that transaction. In the full-detail case, we would want to measure the volume of interactions between the user and various email senders in order to determine which senders receive more immediate actions from the user. With our data, however, we can only measure incoming volume. We can, then, assume that this one-way volume is a good proxy for the type of social features we are attempting to extract from the data.

Clearly this is not ideal. Recall, however, that for this exercise we will be using only the ham messages from the SpamAssassin Public Corpus. If one receives a large volume of ham email messages from a certain address, then it may be that the user has a strong social connection to the sender. Alternatively, it may be the case that the user is signed up to a mailing list with a high volume and would prefer that these emails not receive a high priority. It is exactly for this reason why we must incorporate other features to balance these types of information when developing our ranking system.

One problem with only looking at the volume of messages from a given address is that the temporal component is protracted. Since our data set is static compared to a fully-detailed email log, we must partition the data into temporal segments and measure volume over these periods to get a better understanding of the temporal dynamics.

As we will discuss in detail later, for this exercise we will simply order all of the messages chronologically, then split the set in half. The first half will be used to train the ranking algorithm and the second half to test. As such, message volume from each email address over the entire time period covered by the training data will be used to train our ranker’s social feature.

Given the nature of our data, this may be a good start, but we will need to achieve a deeper understanding if we hope to rank messages more accurately. One way to partition the data to gain a more granular view of these dynamics is to identify conversation threads and then measure the intra-thread activity. (To identify threads, we can borrow techniques used by other email clients and match message subjects with key thread terms, such as “RE:”.) The assumption here is that, although we do not know what actions the user is taking on a thread, if it is very active then it is likely to be more important than less-active threads. By compressing the temporal partitions into these small pieces, we can get a much more accurate proxy for the thread features we need to model email priority.

Next, there are many content features we could extract from the emails to add to our feature set. In this case, we will continue to keep things relatively simple by extending the text mining techniques we used in Chapter 3 to this context. Specifically, if there are common terms in the subjects and bodies of emails received by a user, then future emails that contain these terms in the subject and body may be more important than those that do not. This is actually a common technique, and it is mentioned briefly in the description of Google’s priority inbox. By adding content features based on terms for both the email subject and body, we will encounter an interesting problem of weighting. Typically, there are considerably fewer terms in an email’s subject than the body; therefore, we should not weight the relative importance of common terms in these two features equally.

Finally, there are also many features used in enterprise distributed priority inbox implementations—like Gmail’s—that are simply unavailable to us in this exercise. We have already mentioned that we are blind to much of the social feature set, and therefore must use proxies to measure these interactions. Furthermore, there are many user actions that we do not even have the ability to approximate. For example, user actions such as labeling or moving email messages are completely hidden from our view. In the Google priority inbox implementation, these actions form a large portion of the action set, but are completely missing here. Again, while this is a weakness to the approach described here when compared to those used when full-detail email logs are available, since they are not available in this case, the fact that they are missing will not affect our results.

Figure 4-1. Strategy for extracting priority features from email data

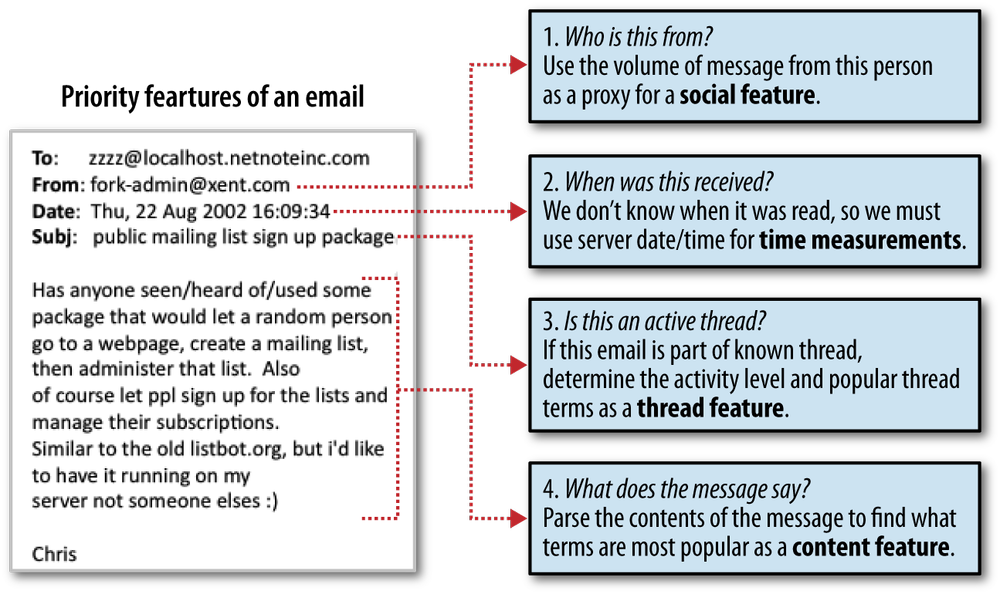
We now have a basic blueprint for the feature set we will use to create our email ranking system. We begin by ordering the messages chronologically, because in this case much of what we are interested in predicting is contained in the temporal dimension. The first half of these messages are used to train our ranker. Next, we have four features we will use during training. The first is a proxy for the social feature, which measures the volume of messages from a given user in the training data. Next, we attempt to compress the temporal measurements by looking for threads, and ranking active threads higher than inactive ones. Finally, we add two content features based on frequent terms in email subjects and message bodies. Figure 4-1 is an illustration of how these features are extracted from an email.

In the next section, we will implement the priority inbox approach described above. Using the features listed here, we will specify a weighting scheme that attempts to quickly push more important messages to the top of the stack. As before, however, our first steps will be to take the raw email data and extract the relevant pieces to fit into our feature set.

Writing a Priority Inbox

By now you will have noticed a trend: before we can get to the sexy parts of machine learning, we need to get our hands dirty hacking at the data to split, pull, and parse it until it’s in a shape fit for our analysis. So far, we have only had to suffer slightly during this process. To build the spam classifier, we only had to extract the email message body, and then we let the tm package do all of the heavy lifting. For this exercise, however, we are adding several other features to our data set and complicating the process by adding a temporal dimension as well. As such, we will have to operate on the data considerably more. But we are hackers, and getting dirty with data is what we like!

For this exercise, we will be focusing on only the ham email messages from the SpamAssassin Public Corpus. Unlike the spam classification exercise, here we are not concerned with the type of email but rather with how each should be ranked in terms of priority. Therefore, we will use the largest easy ham data set, and not worry about including other types of emails. Since we may safely assume a user would not distinguish among emails in this way when determining which emails have a higher priority, there is no reason to carry this information into our ranking system.^[8] Instead, we want to be able to learn as much about our features sets from a single user’s emails, which is why we will use the first easy ham data set emails:

library(tm)
library(ggplot2)

data.path <- "../../03-Classification/code/data/"
easyham.path <- paste(data.path, "easy_ham/", sep="")

Similarly to Chapter 3, the only R packages we will be using in this exercise are tm, for extracting common terms from the emails subjects and bodies, and ggplot2, for visualizing the results. Also, since the SpamAssassin Public Corpus is a relatively large text data set, we will not duplicate it in the data/ folder for this chapter. Instead, we will set the relative path for the data back to its location in the Chapter 3 files.

Next, we will create a series of functions that will work together to parse each email into the feature set illustrated in Figure 4-1. From this diagram we know that we need to extract four elements from each email message: the sender’s address, date received, subject, and message body.

Functions for Extracting the Feature Set

Recall that in Chapter 2, we introduced the idea of data as rectangles. For this exercise, therefore, the task of constructing the training data is one of “rectangularization.” We need to shape the email data set to fit into a usable feature set. The features we extract from the emails will be the columns of our training data, and each row will be the unique values from a single email filling in the rectangle. Conceptualizing data this way is very useful, as we need to take the semi-structured text data in the email messages and turn them into a highly structured training data set that we can use to rank future emails:

parse.email <- function(path) {
    full.msg <- msg.full(path)
    date <- get.date(full.msg)
    from <- get.from(full.msg)
    subj <- get.subject(full.msg)
    msg <- get.msg(full.msg)
    return(c(date, from, subj, msg, path))
}

To explore this process, we will work backwards and begin by examining the parse.email function. This will call a series of helper functions that extract the appropriate data from each message, and then order these elements into a single vector. The vector created by the command c(date, from, subj, msg, path) constitutes the single row of data that will populate our training data. The process of turning each email message into these vectors, however, requires some classic text hacking.

Note

We include the path string as the final column because it will make ordering the data easier during the testing phase.

msg.full <- function(path) {
    con <- file(path, open="rt", encoding="latin1")
    msg <- readLines(con)
    close(con)
    return(msg)
}

If you worked through the entire case study in Chapter 3, the msg.full function above will look very familiar. Here, we are simply opening a connection file path and reading the file’s contents into a character vector. The readLines function will produce a vector whose elements are each line in the file. Unlike what we did in Chapter 3, here we do not preprocess the data at this step because we need to extract various elements from the messages. Instead, we will return the entire email as a character vector and write separate functions to work on this vector to extract the necessary data.

With the message vector in hand, we must begin to fight our way through the data in order to extract as much useable information from the email messages—and organize them in a uniform way—to build our training data. We will begin with the relatively easy task of extracting the sender’s address. To do this—and all of the data extraction in this section—we need to identify the text patterns in the email messages that identify the data we are looking for. To do so, let’s take a look at a few email messages.

Example 4-1. Examples of email “From” text pattern variation

Email #1
........................................................
X-Sender: [e-mail] (Unverified)
Message-Id: <p05100300ba138e802c7d@[194.154.104.171]>
To: Yahoogroups Forteana <[e-mail]>
From: Joe McNally <[e-mail]>
X-Yahoo-Profile: wolf_solent23
MIME-Version: 1.0
Mailing-List: list [e-mail]; contact
    [e-mail]
........................................................

Email #2         
........................................................
Return-Path: [e-mail]
Delivery-Date: Fri Sep  6 17:27:57 2002
From: [e-mail] (Paul Svensson)
Date: Fri, 6 Sep 2002 12:27:57 -0400 (EDT)
Subject: [Spambayes] Corpus Collection (Was: Re: Deployment)
In-Reply-To: <[e-mail]>
Message-ID: <[e-mail]>
........................................................

After exploring a few email messages, we can observe key patterns in the text that identify the sender’s email address. Example 4-1 shows two excerpts from emails that highlight these patterns. First, we need to identify the line in each message that contains the email address. From the examples above, we can see that this line always has the term “From:”, which again, is specified by the email protocol mentioned in Chapter 3. So, we will use this information to search the character vector for each email to identify the correct element. As we can see from Example 4-1, however, there is variation in how the email address is written among emails. This line always contains the name of the sender and the sender’s email address, but sometimes encapsulated in angled brackets (Email #1) while in others it is not enclosed in brackets (Email #2). For that reason, we will write a get.from function that uses regular expressions to extract the data for this feature:

get.from <- function(msg.vec) {
    from <- msg.vec[grepl("From: ", msg.vec)]
    from <- strsplit(from, '[":<> ]')[[1]]
    from <- from[which(from !="" & from !=" ")]
    return(from[grepl("@", from)][1])
}

As we have already seen, R has many powerful functions for working with regular expressions. The grepl function works just like a regular grep function for matching regular expression patterns, but the “l” stands for logical. So, rather than returning vector indices, it will return a vector of the same length as msg.vec with boolean values indicating whether the pattern was matched in the character vector. After the first line in this function, the from variable is a character vector with a single element: the “From:” lines highlighted in Example 4-1.

Now that we have the correct line, we need to extract the address itself. To do this, we will use the strsplit function, which will split a character element into a list by a given regular expression pattern. In order to properly extract the addresses, we need to account for the variation in the text patterns observed in Example 4-1. To do so, we create a set of characters for our pattern by using the square brackets. Here, the characters we want to split the text by are colons, angle brackets, and an empty character. This pattern will always put the address as the first element in the list, so we can pull that from the list with [[1]]. Because of the variation in the pattern, however, it will also add empty elements to this vector. In order to return only the email address itself, we will ignore those empty elements, then look for the remaining element containing the “@” symbol, and return that. We now have parsed 1/4 of the data needed to generate our training data.

Extracting the next two features, the message subject and body, is relatively simple. In Chapter 3, we needed to extract the message body in order to quantify the terms in spam and ham email messages. The get.msg function, therefore, simply replicates the pattern we used to perform the same task here. Recall, the message body always appears after the first empty line break in the email. So, we simply look for the first empty element in msg.vec and return all of the elements after that. To simplify the text mining process, we collapse these vectors into a single character vector with the paste function and return that:

get.msg <- function(msg.vec) {
    msg <- msg.vec[seq(which(msg.vec == "")[1] + 1, length(msg.vec), 1)]
    return(paste(msg, collapse="\n"))
}

Extracting the email’s subject is akin to extracting the sender’s address, but is actually a bit simpler. With the get.subject function we will again use the grepl function to look for the “Subject:” pattern in each email to find the line in the message that contains the subject. There is, however, a catch: as it turns out, not every message in the data set actually has a subject. As such, the pattern matching we are using will blow up on these edge cases. In order to guard against this, we will simply test to see if our call to grepl has actually returned anything. To test this, we check that the length of subj is greater than zero. If it is, we split the line based on our pattern and return the second element. If not, we return an empty character. By default in R, when matching functions like grepl do not make a match, special values such as integer(0) or character(0) will be returned. These values have a zero length, so this type of check is always a good idea when running a function over a lot of messy data:

get.subject <- function(msg.vec) {
    subj <- msg.vec[grepl("Subject: ", msg.vec)]
    if(length(subj) > 0) {
        return(strsplit(subj, "Subject: ")[[1]][2])
    }
    else {
        return("")
    }
}

Warning

In the code/data/hard_ham/ folder in the files for Chapter 3, see file 00175.* for a problematic email message. As is often the case when attempting to work a data set into your problem, you will run into edge cases like this. Getting through them will take some trial and error, as it did for us in this case. The important thing is to stay calm and dig deeper into the data to find the problem. You’re not doing it right if you do not stumble on your way to parsing a data set into a workable form!

We now have three-quarters of our features extracted, but it is the final element—the date and time the message was received—that will cause us to suffer the most. This field will be difficult to work with for two reasons. First, dealing with dates is almost always a painful prospect, as different programming languages often have slightly different ways of thinking about time; and, in this case, R is no different. Eventually, we will want to convert the date strings into POSIX date objects in order to sort the data chronologically. But to do this, we need a common character representation of the dates, which leads directly to the second reason for our suffering: there is considerable variation within the SpamAssassin Public Corpus in how the dates and times messages received are represented. Example 4-2 illustrates a few examples of this variation.

Example 4-2. Examples of email date and time received text pattern variation

Email #1
........................................................
Date: Thu, 22 Aug 2002 18:26:25 +0700

    Date:        Wed, 21 Aug 2002 10:54:46 -0500
    From:        Chris Garrigues lt;[e-mail];
    Message-ID:  lt;[e-mail];
........................................................

Email #2 
........................................................
List-Unsubscribe: lt;https://example.sourceforge.net/lists/listinfo/sitescooper-talkgt;,
    lt;mailto:[e-mail]?subject=unsubscribegt;
List-Archive: lt;http://www.geocrawler.com/redir-sf.php3?list=sitescooper-talkgt;
X-Original-Date: 30 Aug 2002 08:50:38 -0500
Date: 30 Aug 2002 08:50:38 -0500
........................................................

Email #3
........................................................
Date: Wed, 04 Dec 2002 11:36:32 GMT
Subject: [zzzzteana] Re: Bomb Ikea
Reply-To: [e-mail]
Content-Type: text/plain; charset=US-ASCII
........................................................

Email #4
........................................................
Path: not-for-mail
From: Michael Hudson lt;[e-mail];
Date: 04 Dec 2002 11:49:23 +0000
Message-Id: lt;[e-mail];
........................................................

As you can see, there are many things that we need to be cognizant of when extracting the date and time information from each email. The first thing to notice from the examples in Example 4-2 is that the data we want to extract is always identified by “Date:”. However, there are many traps in using this pattern that we must be mindful of. As Email #1 from Example 4-2 illustrates, sometimes there will be multiple lines that match this pattern. Likewise, Email #2 shows that some lines may be partial matches, and in either case the data on these lines can be conflicting—as it is in Email #1. Next, we can observe even in these three examples that dates and times are not stored in a uniform way across all emails. In all emails, there are extraneous GMT offsets and other types of labeling information. Finally, the format for the date and time in Email #4 is totally different from the previous two.

All of this information will be critical in getting the data into a uniform and workable form. For now, however, we will only need to focus on extracting the date and time information without the extraneous offset information by defining a get.date function. Once we have all of the date/time strings, we will need to deal with converting the conflicting date/time formats to a uniform POSIX object, but this will not be handled by the get.date function:

get.date <- function(msg.vec) {
    date.grep <- grepl("^Date: ", msg.vec)
    date.grepl <- which(date.grep == TRUE)
    date <- msg.vec[date.grep[1]]
    date <- strsplit(date, "\\+|\\-|: ")[[1]][2]
    date <- gsub("^\\s+|\\s+$", "", date)
    return(strtrim(date, 25))
}

As we mentioned, many emails have multiple full or partial matches to the “Date:” pattern. Notice, however, from Emails #1 and #2 in Example 3-1 that only one line from the email has “Date:” at the start of the string. In email #1, there are several empty characters preceding this pattern, and in #2 the pattern is partially matched to “X-Original-Date:”. We can force the regular expression to match only strings that have “Date:” at the start of the string by using the caret operator (“^Date:”). Now, grepl will only return TRUE when that pattern starts an element of the message vector.

Next, we want to return the first element in msg.vec that matches this pattern. We may be able to get away with simply returning the element in msg.vec that matches our pattern in grepl, but what if an email message contains a line that begins “Date:”? If this edge case were to occur, we know the first element that matched our pattern will come from the message’s header because header information always comes before the message body. To prevent this problem, we always return the first matching element.

Now we need to process this line of text in order to return a string that can eventually be converted into a POSIX object in R. We’ve already noted that there is extraneous information and that the dates and times are not stored in a uniform format. To isolate the date and time information, we will split the string by characters that denote extraneous information. In this case, that will be a colon, a plus, or a minus character. In most cases, this will leave us with only the date and time information, plus some trailing empty characters. The use of the gsub function in the next line will substitute any leading or training whitespace in the character string. Finally, to deal with the kind of extraneous data we observe in Email #3 in Example 4-2, we will simply trim off any characters after a 25 character limit. A standard data/time string is 25 characters long, so we know that anything over this is extraneous.

easyham.docs <- dir(easyham.path)
easyham.docs <- easyham.docs[which(easyham.docs != "cmds")]
easyham.parse <- lapply(easyham.docs, function(p) 
    {parse.email(paste(easyham.path, p, sep=""))})


ehparse.matrix <- do.call(rbind, easyham.parse)
allparse.df <- data.frame(ehparse.matrix, stringsAsFactors=FALSE)
names(allparse.df) <- c("Date", "From.EMail", "Subject", "Message", "Path")

Congratulations, you have successfully suffered though transforming this amorphous set of emails into a structured rectangle suitable for training our ranking algorithm! Now all we have to do is throw the switch. Similar to what we did in Chapter 3, we will create a vector with all of the “easy ham” files, remove the extra “cmds” file from the vector, and then use the lapply function to apply the parse.email function to each email file. Because we are pointing to files in the data directory for the previous chapter, we also have to be sure to concatenate the relative path to these files using the paste function and our easyham.path inside the lapply call.

Next, we need to convert the list of vectors returned by lapply into a matrix—i.e., our data rectangle. As before, we will use the do.call function with rbind to create the ehparse.matrix object. We will then convert this to a data frame of character vectors, and then set the column names to c("Date", "From.EMail", "Subject", "Message", "Path"). To check the results, use head(allparse.df) to inspect the first few rows of the data frame. We will not reproduce this here to conserve space, but we recommend you do.

Before we can proceed to creating a weighting scheme from this data, however, there is still some remaining housekeeping.

As we mentioned, our first trial with extracting the dates was simply isolating the text. Now, we need to take that text and convert it into POSIX objects that can be compared logically. This is necessary because we need to sort the emails chronologically. Recall that running through this entire exercise is the notion of time, and how temporal differences among observed features can be used to infer importance. The character representation of dates and times will not suffice.

As we saw in Example 4-2, there are two variations on the date format. From these examples, Email #3 has a date/time string of the format “Wed, 04 Dec 2002 11:36:32,” while Email #4 is of the format “04 Dec 2002 11:49:23”. To convert these two strings into POSIX formats, we will need to use the strptime function, but pass it two different date/time formats to make the conversion. Each element of these strings matches a specific POSIX format element, so we will need to specify conversion strings that match these variants:

date.converter <- function(dates, pattern1, pattern2) {
    pattern1.convert <- strptime(dates, pattern1)
    pattern2.convert <- strptime(dates, pattern2)
    pattern1.convert[is.na(pattern1.convert)] <- pattern2.convert[is.na(pattern1.convert)]
    return(pattern1.convert)
}

pattern1 <- "%a, %d %b %Y %H:%M:%S"
pattern2 <- "%d %b %Y %H:%M:%S"

allparse.df$Date <- date.converter(allparse.df$Date, pattern1, pattern2)

Note

R uses the standard POSIX date/time format strings to make these conversions. There are many options for these strings, and we recommend reading through the documentation in the strptime function using the ?strptime command to see all of the options. Here we will only be using a select few, but understanding them in greater depth will be very useful whenever working with dates and times in R.

We need to convert the strings in the Date column of allparse.df to the two different POSIX formats separately, then recombine them back into the data frame to complete the conversion. To accomplish this, we will define the date.converter function to take two different POSIX patterns and a character vector of date strings. When the pattern passed to strptime does not match the string passed to it, the default behavior is to return NA. We can use this to recombine the converted character vectors by replacing the elements with NA from the first conversion with those from the second. Because we know there are only two patterns present in the data, the result will be a single vector with all date strings converted to POSIX objects.

The final bit of cleanup is to convert the character vectors in the Subject and From email columns to all lowercase. Again, this is done to ensure that all data entries are as uniform as possible before we move into the training phase. Next, we sort the data chronologically using a combination of the with and order commands in R. (R has a particularly unintuitive way of doing sorting, but this shorthand is something you will find yourself doing very often, so it is best to get familiar with it.) The combination will return a vector of the element indices in ascending chronological order. Then, to order the data frame by these indices, we need to reference the elements of allparse.df in that order, and add the final comma before closing the square bracket so all columns are sorted this way:

allparse.df$Subject <- tolower(allparse.df$Subject)
allparse.df$From.EMail <- tolower(allparse.df$From.EMail)

priority.df <- allparse.df[with(allparse.df, order(Date)),]

priority.train <- priority.df[1:(round(nrow(priority.df) / 2)),]

Finally, we store the first half of the chronologically-sorted data frame as priority.traning. The data in this data frame will be used to train our ranker. Later, we will use the second half of priority.df to test the ranker. With the data fully formed, we are ready to begin designing our ranking scheme. Given our feature set, one way to proceed is to define weights for each observed feature in the training data.

Creating a Weighting Scheme for Ranking

Before we can proceed to implementing a weighting scheme, we need to take a brief digression to discuss scales. Consider for a moment your own email activity. Do you interact with roughly the same people on a regular basis? Do you know about how many emails you receive in a day? How many emails do you receive from total strangers in a week? If you are like us, and we suspect most other people, your email activity crudely adheres to the 80/20 cliche. That is, about 80% of your email activity is conducted with about 20% of the total number of people in your address book. So, why is this important?

We need to be able to devise a scheme for weighting the observation of certain features in our data, but because of the potential differences in scale among these observations, we cannot compare them directly. More precisely, we cannot compare their absolute values directly. Let’s take the training data that we have just finished parsing. We know that one of the features that we are adding to our ranker is an approximation of social interaction based on the volume of emails received from each address in our training data.

To begin to explore how this scaling affects our first feature, we will need to count the number of times each email address appears in our data. To do this, we will use the plyr package, which we have already loaded in as a dependency for ggplot2. If you worked through the example in Chapter 1, then you have already seen plyr in action. Briefly, the family of functions in plyr are used to chop data into smaller squares and cubes so that we can operate over these pieces all once. (This is very similar to the popular Map-Reduce paradigm used in many large-scale data analysis environments.) Here, we will be performing a very simple task: find all of the columns with matching addresses in the From.EMail column and count them.

To do this, we use the ddply function, which operates on data frames, with our training data. The syntax has us define the data grouping we want first—which in this case in only the From.EMail dimension—then the operation we will run over that grouping. Here, we will use the summarise option to create a new column named Freq with the count information. You can use the head(from.weight) command to inspect the results:

from.weight <- ddply(priority.train, .(From.EMail), summarise, Freq=length(Subject))

Note

In this case, the operation asks for the length of the vector at column Subject in the chopped up data frame, but we could have actually used any column name from the training data to get the same result, because all columns matching our criteria will have the same length. Becoming more familiar with plyr for manipulating data will be extremely valuable to you going forward, and we highly recommend the package author’s documentation HW11.

Figure 4-2. Number of emails received from various senders in training data

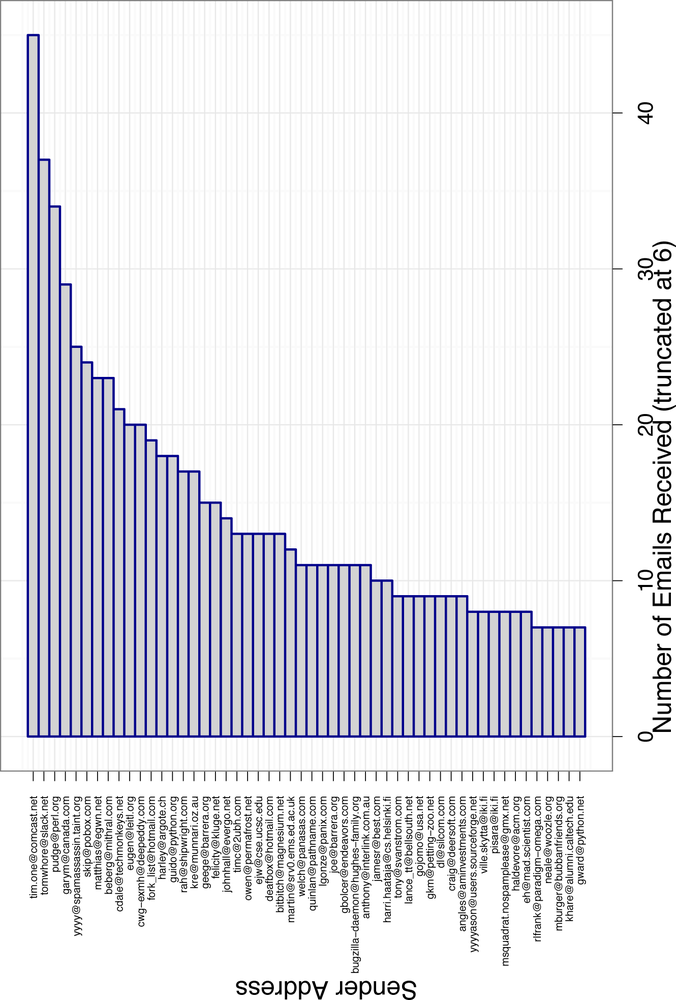
To get a better sense of the scale of this data, let’s plot the results. Figure 4-2 shows a bar chart of the volume of emails from users who have sent more than six emails. We have performed this truncation to make it easier to read, but even with this data removed, we can already see how quickly the data scales. The top emailer, [e-mail], has sent 45 messages in our data. That’s about 15 times more emails than the average person in our training data! But [e-mail] is pretty unique. As you can see from Figure 4-2, there are only a few other senders near his level, and the frequency drops off very quickly after them. How could we weight an observation from an average person in our training data without skewing that value to account for outliers like our top emails?

A Log-Weighting Scheme

The answer comes in transforming the scales. We need to make the numerical relationship among the units in our feature set less extreme. If we compare the absolute frequency counts, then an email from [e-mail] will be weighted as 15 times more important than email from an average sender. This is very problematic, as we will eventually want to establish a threshold for being either priority or not based on the range of weight values produced by our ranker at the learning stage. With such extreme skewness, our threshold will either be far too low or far too high, so we need to rescale the units in order to account for the nature of our data.

This brings us to logarithms and log-transformations. You are probably familiar with logarithms from elementary mathematics, but if not, the concept is quite simple. A logarithm is a function that returns the exponent value that would satisfy an equation where some base number is being raised to that exponent equals the number given to the logarithmic function.

The base value in a log-transformation is critical. As hackers, we are familiar with thinking of things in base two, or binary. We may very easily construct a log-transformation of base two. In this case, we would solve an equation for the exponent value where the input value is equal to two raised to that exponent. For example, if we transformed 16 by log base-two, it would equal four, because two raised to the 4th power equals 16. In essence, we are “reversing” an exponential, so these types of transformations work best when the data fit such a function.

Figure 4-3. A natural-log spiral, often observed in nature

The two most common log-transformations are the so-called natural log and the log base-10 transformation. In the former, the base is the special value e, which is an irrational constant (like pi) equal to approximately 2.718. The name natural log is often denoted ln. Rates of change equal to this constant are very often observed in nature, and in fact the derivation can be done geometrically as a function of the angles inside a circle. You are likely very familiar with shapes and relationships that follow a natural log, although you may not have thought of them in these terms. Figure 4-3 illustrates a natural log spiral, which can be observed in many naturally-occurring phenomenon. Some examples include the interior structure of a nautilus shell, the spiraling winds of a hurricane (or tornado)—even the scattering of interstellar particles in our galaxy follow a natural logarithmic spiral. Also, many professional camera settings’ apertures are set to vary by natural logs.

Given the intimate relationship between this value and many naturally occurring phenomena, it is a great function for re-scaling social data—like email activity—that is exponential. Alternatively, the log base-10 transformation, often denoted log10, replaces the e value in the natural log-transform with a 10. Given how log-transforms work, we know that the log base-10 transformation will reduce large values to much smaller ones than the natural log. For example, the log base-10 transformation of 1,000 is 3; because 10 raised to the third is 1,000, while the natural log is approximately 6.9. Therefore, it makes sense to use a log base-10 transformations when our data scale by a very large exponent.

Figure 4-4. Number of emails received, with absolute counts, and ln and log10 transformation

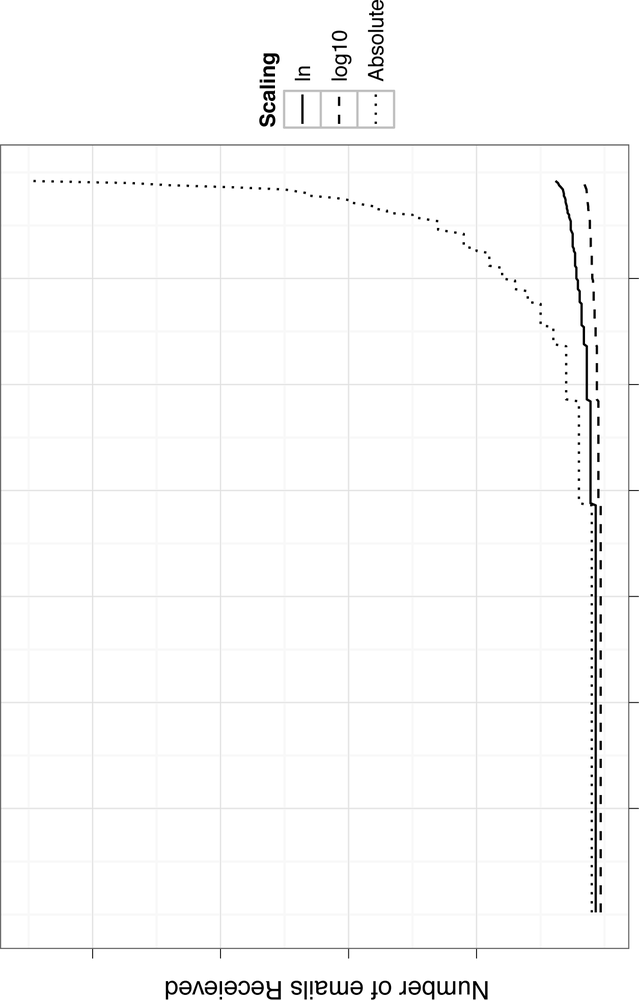
The ways in which both of these options would transform our email volume data are illustrated in Figure 4-4. In this figure, we can see that the volume of emails sent by the users in the training data follows a fairly steep exponential. By transforming those values by the natural log and log base-10, we significantly flatten out that line. As we know, the log base-10 transforms the values substantially, while the natural log still provides some variation that would allow us to pull out meaningful weights from this training data. For this reason, we will use the natural log to define the weight for our email volume feature:

from.weight <- transform(from.weight, Weight=log(Freq + 1))

Note

As we have done here, and as we explained in detail in Chapter 2, it is always a good idea to explore your data visually as you are working through any machine learning problem. We want to know how all of the observations in our feature set relate to one another in order to make the best predictions. Often, the best way to do this is through data visualization.

Finally, recall from grade school mathematics your rules for exponents. Anything raised to zero always equals one. This is very important to keep in mind when using log-transformation in a weighting scheme, because any observation equal to one will be transformed to zero. This is problematic in a weighting scheme, because multiplying other weights with zero will zero out the entire value. To avoid this, we always add one to all observations before taking logs.

Note

There is actually a function in R called log1p that computes log(1 + p), but for the purposes of learning and being explicit we will do this addition “by hand.”

Given the rescaling, this does not affect our results, and it keeps all weights greater than zero. In this case, we are using the default base value for the log function, which is the natural log.

Warning

For our purposes we will never have an observation in our feature set that is equal to zero, because we are counting things. If there are no observations of something, then it simply doesn’t enter our training data. In some cases, however, this will not be true, and you may have zero observations in your data. The log of zero is undefined, and if you try to compute it in R, it will return the special value -Inf. Often, having instances of -Inf in your data with cause things to blow up.

Weighting from Email Thread Activity

The second feature we want to extract from the data is email thread activity. As noted, we have no way of knowing whether the user we are building this ranking for has responded to any emails, but we can group messages by their thread and measure how active they have been since they started. Again, our assumption in building this feature is that time is important, and therefore threads that have more messages sent over a short period of time are more active and consequently more important.

The emails in our data set do not contain specific thread IDs, but a logical way to identify threads within the training data is to look for emails with a shared subject line. That is, if we find a subject that begins with “re: ”, then we know that this is part of some thread. When we see a message like this, we can look around for other messages in that thread and measure the activity.

find.threads <- function(email.df) {
    response.threads <- strsplit(email.df$Subject, "re: ")
    is.thread <- sapply(response.threads, function(subj) ifelse(subj[1] == "", 
                                                                TRUE, 
                                                                FALSE))
    threads <- response.threads[is.thread]
    senders <- email.df$From.EMail[is.thread]
    threads <- sapply(threads, function(t) paste(t[2:length(t)], collapse="re: "))
    return(cbind(senders,threads))
}

threads.matrix<-find.threads(priority.train)

This is precisely what the find.threads function attempts to do with our training data. If we split every subject in our training data by “re:”, then we can find threads by looking for split character vectors with an empty character as the first element. Once we know which observations in the training data are part of threads, we can extract the senders from those threads and the subject. The result matrix will have all of the senders and initial thread subject in our training data.

email.thread <- function(threads.matrix) {
    senders <- threads.matrix[, 1]
    senders.freq <- table(senders)
    senders.matrix <- cbind(names(senders.freq), senders.freq, log(senders.freq + 1))
    senders.df <- data.frame(senders.matrix, stringsAsFactors=FALSE)
    row.names(senders.df) <- 1:nrow(senders.df)
    names(senders.df) <- c("From.EMail", "Freq", "Weight")
    senders.df$Freq <- as.numeric(senders.df$Freq)
    senders.df$Weight <- as.numeric(senders.df$Weight)
    return(senders.df)
}

senders.df <- email.thread(threads.matrix)

Now, we will create a weighting based on the senders who are most active in threads. This will be a supplement to the volume-based weighting we just did for the entire data set, but now we will focus only on those senders present in the threads.matrix. The function email.thread will take the threads.matrix as input and generate this secondary volume-based weighting. This will be very similar to what we did in the previous section, except this time we will use the table function to count the frequency of senders in the threads. This is done simply to show a different method for accomplishing the same calculation on a matrix in R, rather than a data frame using plyr. Most of this function simply performs housekeeping on the senders.df data frame, but notice that we are again using a natural-log weighting.

As the final piece to the email thread feature, we will create a weighting based on threads that we know are active. We have already identified all of the threads in our training data and created a weighting based on the terms in those threads. Now, we want to take that knowledge and give additional weight to known threads that are also active. The assumption here is that if we already know the threads, we expect a user to place more importance on those threads that are more active.

Using the threads.matrix we just created, we will go back into the training data to find all of the emails inside each thread. To do this, we create the get.threads function, which will take the threads.matrix and out training data as arguments. Using the unique command, we create a vector of all thread subjects in our data. Now we need to take this information and measure each thread’s activity:

get.threads <- function(threads.matrix, email.df) {
    threads <- unique(threads.matrix[, 2])
    thread.counts <- lapply(threads, function(t) thread.counts(t, email.df))
    thread.matrix <- do.call(rbind, thread.counts)
    return(cbind(threads, thread.matrix))
}

thread.counts <- function(thread, email.df) {
    thread.times <- email.df$Date[which(email.df$Subject == thread 
    | email.df$Subject == paste("re:", thread))]
    freq <- length(thread.times)
    min.time <- min(thread.times)
    max.time <- max(thread.times)
    time.span <- as.numeric(difftime(max.time, min.time, units="secs"))
    if(freq < 2) {
        return(c(NA,NA,NA))
    }
    else {
        trans.weight <- freq / time.span
        log.trans.weight <- 10 + log(trans.weight, base=10)
        return(c(freq,time.span, log.trans.weight))
    }
}

thread.weights <- get.threads(threads.matrix, priority.train)
thread.weights <- data.frame(thread.weights, stringsAsFactors=FALSE)
names(thread.weights) <- c("Thread","Freq","Response","Weight")
thread.weights$Freq <- as.numeric(thread.weights$Freq)
thread.weights$Response <- as.numeric(thread.weights$Response)
thread.weights$Weight <- as.numeric(thread.weights$Weight)
thread.weights <- subset(thread.weights, is.na(thread.weights$Freq) == FALSE)

The thread.counts functions will do this. Using the thread subject and training data as parameters, we will collect all of the date and time stamps for all emails matching the thread in the thread.times vector. We can measure how many emails have been received in training data for this thread by measuring the length of thread.times.

Finally, to measure the activity level, we need to know how long the thread has existed in our training data. Implicitly, there is truncation on either side of this data. That is, there may be emails that were received in a thread before our training data started or after. There is nothing we can do about this, so we will take the minimum and maximum date/times for each thread and use these to measure the timespan. The function difftime will calculate the amount of time elapsed between two POSIX objects in some units. In our case, we want the smallest unit possible: seconds.

Due to the truncation, it may be that we observe only a single message in a thread. This could be a thread that ended just as the training data got collected or just started when collection ended. Before we can create a weight based on the activity over the timespan of a thread, we must flag those threads for which we have only one message. The if-statement at the end of thread.counts does this check and returns a vector of NA if the current thread has only one message. We will use this later to scrub these from the activity weighting data.

The final step is to create a weighting for those messages we can measure. We start by calculating the ratio of messages-to-seconds elapsed in the thread. So, if a message were sent every second in a given thread, the result would be one. Of course, in practice, this number is much lower, with the average number of messages in each thread about 4.5 and the average elapsed time about 31,000 seconds (8.5 hours). Given these scales, the vast majority of our ratios are tiny fractions. As before, we still want to transform these values using logs, but because we are dealing with fractional values, this will result in negative numbers. We cannot have a negative weight value in our scheme, so we will have to perform an additional transformation that is formally called an affine transformation.

An affine transformation is simply a linear movement of points in space. Imagine a square drawn on piece of graph paper. If you wanted to move that square to another position on the paper, you could do so by defining a function that moved all of the points in the same direction. This is an affine transformation. To get non-negative weights in log.trans.weight, we will simply add 10 to all the log-transformed values. This will insure that all of the values will be proper weights with a positive value.

As before, once we have generated the weight data with the get.threads and thread.counts, we will perform some housekeeping on the thread.weights data frame to keep the naming consistent with the other weight data frames. In the final step, we use the subset function to remove any rows that refer to threads with only one message (i.e., truncated threads). We can now use head(thread.weights) to check the results:

head(thread.weights)
                                      Thread Freq Response   Weight
1   please help a newbie compile mplayer :-)    4    42309 5.975627
2                 prob. w/ install/uninstall    4    23745 6.226488
3                       http://apt.nixia.no/   10   265303 5.576258
4         problems with 'apt-get -f install'    3    55960 5.729244
5                   problems with apt update    2     6347 6.498461
6 about apt, kernel updates and dist-upgrade    5   240238 5.318328

The first two rows are good examples of how this weighting scheme values thread activity. In both of these threads, there have been four messages. The prob. w/ install/uninstall thread, however, has been in the data for about half as many seconds. Given our assumptions, we would think that this thread is more important and therefore should have a higher weight. In this case, we give messages form this thread about 1.04 times more weight than those from the please help a newbie compile mplayer :-) thread. This may or may not seem reasonable to you and therein lies part of the art in designing and applying a scheme such as this to a general problem. It may be that in this case, our user would not value things this way (while others might), but because we want a general solution, we must accept the consequences of our assumptions.

The final weighting data we will produce from the threads are the frequent terms in these threads. Similar to what we did in Chapter 3, we create a general function term.counts that takes a vector of terms and a TermDocumentMatrix control list to produce the TDM and extract the counts of terms in all of the threads. The assumption in creating this weighting data is that frequent terms in active thread subjects are more important than terms that are either less frequent or not in active threads. We are attempting to add as much information as possible to our ranker in order to create a more granular stratification of emails. To do so, rather than look only for already-active threads, we want to also weight threads that “look like” previously active threads, and term weighting is one way to do this:

term.counts <- function(term.vec, control) {
    vec.corpus <- Corpus(VectorSource(term.vec))
    vec.tdm <- TermDocumentMatrix(vec.corpus, control=control)
    return(rowSums(as.matrix(vec.tdm)))
}

thread.terms <- term.counts(thread.weights$Thread, 
  control=list(stopwords=stopwords()))
thread.terms <- names(thread.terms)

term.weights <- sapply(thread.terms, 
  function(t) mean(thread.weights$Weight[grepl(t, thread.weights$Thread, 
                   fixed=TRUE)]))
term.weights <- data.frame(list(Term=names(term.weights), Weight=term.weights), 
  stringsAsFactors=FALSE, row.names=1:length(term.weights))

The final weighting data we will build is based on term frequency in all email messages in the training data. This will proceed almost identically to our method for counting terms in the spam classification exercise; however, this time we will assign log-transformed weights based on these counts. As with the term-frequency weighting for thread subjects, the implicit assumption in the msg.weights data frame is that a new message that looks like other messages we have seen before is more important than a message that is totally foreign to us:

msg.terms <- term.counts(priority.train$Message, 
    control=list(stopwords=stopwords(),
    removePunctuation=TRUE, removeNumbers=TRUE))

msg.weights <- data.frame(list(Term=names(msg.terms), 
    Weight=log(msg.terms, base=10)), stringsAsFactors=FALSE,
    row.names=1:length(msg.terms))

msg.weights <- subset(msg.weights, Weight > 0)

We now have five weight data frames with which to perform our ranking! This includes from.weight (social activity feature), senders.df (sender activity in threads), thread.weights (thread message activity), term.weights (terms from active threads), and msg.weights (common terms in all emails). We are now ready to run our training data through the ranker to find a threshold for marking a message as important.

Training and Testing the Ranker

To generate a priority rank for each message in our training data, we must multiply all of the weights produced in the previous section. This means that for each message in the data, we will need to parse the email, then take the extracted features and match them to corresponding weight data frames to get the appropriate weighting value. We will then take the product of these values to produce a single—and unique—rank value for each message. The rank.message function below is a single function that takes a file path to a message and produces a priority ranking for that message based on the features we have defined and their subsequent weights. The rank.message function relies on many functions we have already defined, as well as a new function, get.weights (which does the weight lookup when the feature does not map to a single weight—i.e., subject and message terms):

get.weights <- function(search.term, weight.df, term=TRUE) {
    if(length(search.term) > 0) {
        if(term) {
            term.match <- match(names(search.term), weight.df$Term)
        }
        else {
            term.match <- match(search.term, weight.df$Thread)
        }
        match.weights <- weight.df$Weight[which(!is.na(term.match))]
        if(length(match.weights) > 1) {
            return(1)
        }
        else {
            return(mean(match.weights))
        }
    }
    else {
        return(1)
    }
}

We first define get.weights, which takes three arguments: some search terms (a string), the weight data frame in which to do the look up, and a single Boolean value term. This final parameter will allow us to tell the application if it is doing a lookup on a term data frame or on a thread data frame. We will treat these lookups slightly differently due to differences in column labels in the thread.weights data frame, so we need to make this distinction. The process here is fairly straightforward, as we use the match function to find the elements in the weight data frame that match search.term and return the weight value. What is more important to notice here is how the function is handling non-matches.

First, we do one safety check to be sure that the search term being passed to get.weights is valid by checking that it has some positive length. This is the same type of check we performed while parsing the email data to check that an email actually had a subject line. If it is an invalid search term, then we simply return a 1 (which elementary mathematics tells us will not alter the product computed in the next step because of the rules for multiplication by 1). Next, the match function will return an NA value for any elements in the search vector that do not match search.term. Therefore, we extract the weight values for only those matched elements that are not NA. If there are no matches, the term.match vector will be all NA’s, in which case match.weights will have a zero length. So, we do an additional check for this case, and if we encounter this case we again return 1. If we have matched some weight values, we return the mean of all these weights as our result.

The rank.message function uses similar rules to the get.weights function for assigning weight values to the features extracted from each email in the data set. First, it calls the parse.email function to extract the four features of interest. It then proceeds to use a series of if-then clauses to determine whether any of the features extracted from the current email are present in any of the weight data frames used to rank and assigns weights appropriately. The from and thread.from use the social interaction features to find weight based on the sender’s email address. Note that, in both cases, if the ifelse function does not match anything in the data weight data frames, a 1 is returned. This is the same strategy implemented in the get.weights function:

rank.message <- function(path) {
    msg <- parse.email(path)
    # Weighting based on message author

    # First is just on the total frequency
    from <- ifelse(length(which(from.weight$From.EMail == msg[2])) > 0,
        from.weight$Weight[which(from.weight$From.EMail == msg[2])], 1)

    # Second is based on senders in threads, and threads themselves
    thread.from <- ifelse(length(which(senders.df$From.EMail == msg[2])) > 0,
        senders.df$Weight[which(senders.df$From.EMail == msg[2])], 1)

    subj <- strsplit(tolower(msg[3]), "re: ")
    is.thread <- ifelse(subj[[1]][1] == "", TRUE, FALSE)
    if(is.thread) {
        activity <- get.weights(subj[[1]][2], thread.weights, term=FALSE)
    }
    else {
        activity <- 1
    }

    # Next, weight based on terms    

    # Weight based on terms in threads
    thread.terms <- term.counts(msg[3], control=list(stopwords=stopwords()))
    thread.terms.weights <- get.weights(thread.terms, term.weights)
    
    # Weight based terms in all messages
    msg.terms <- term.counts(msg[4], control=list(stopwords=stopwords(),
        removePunctuation=TRUE, removeNumbers=TRUE))
    msg.weights <- get.weights(msg.terms, msg.weights)

    # Calculate rank by interacting all weights
    rank <- prod(from, thread.from, activity, 
        thread.terms.weights, msg.weights)

    return(c(msg[1], msg[2], msg[3], rank))
}

For the thread- and term-based weighting, some internal text parsing is done. For threads, we first check that the email being ranked is part of a thread in the exact same way we did during the training phase. If it is, we look up a rank; otherwise, we assign 1. For term-based weighting, we use the term.counts function to get the terms of interest from the email features and then weight accordingly. In the final step, we generate the rank by passing all of the weight values we have just looked up to the prod function. The rank.message function then returns a vector with the email’s data/time, sender’s address, subject, and rank.

We are now ready to fire up our ranker! Before we can proceed, we will split our data into two chronologically divided sets. The first will be the training data, which we call train.paths. We will use the ranking data generated from here to establish a threshold value a “priority” message. Once we have this, we can run the ranker over the emails in test.paths to determine which ones are priority and to estimate their internal rank ordering. Next, we will apply the rank.messages function to the train.paths vector to generate a list of vectors containing the features and priority rank for each email. We then perform some basic housekeeping to convert this list to a matrix. Finally, we we convert this matrix to a data frame with column names and properly-formatted vectors:

train.paths <- priority.df$Path[1:(round(nrow(priority.df) / 2))]
test.paths <- priority.df$Path[((round(nrow(priority.df) / 2)) + 1):nrow(priority.df)]

train.ranks <- lapply(train.paths, rank.message)
train.ranks.matrix <- do.call(rbind, train.ranks)
train.ranks.matrix <- cbind(train.paths, train.ranks.matrix, "TRAINING")
train.ranks.df <- data.frame(train.ranks.matrix, stringsAsFactors=FALSE)
names(train.ranks.df) <- c("Message", "Date", "From", "Subj", "Rank", "Type")
train.ranks.df$Rank <- as.numeric(train.ranks.df$Rank)

priority.threshold <- median(train.ranks.df$Rank)

train.ranks.df$Priority <- ifelse(train.ranks.df$Rank >= priority.threshold, 1, 0)

Warning

You may notice that train.ranks <- lapply(train.paths, rank.message) causes R to throw a warning. This is not a problem, but simply a result of the way we have built the ranker. You may wrap the lapply call in the suppressWarnings function if you wish to turn off this warning.

We now perform the critical step of calculating a threshold value for priority email. As you can see, for this exercise we have decided to use the median rank value as our threshold. Of course, we could have used many other summary statistics for this threshold, as we discussed in Chapter 2. Because we are not using pre-existing examples of how emails ought to be ranked to determine this threshold, we are performing a task that is not really a standard sort of supervised learning. But we have chosen the median for two principled reasons. First, if we have designed a good ranker, then the ranks should have a smooth distribution, with most emails having low rank and many fewer emails having a high rank. We are looking for “important emails,” i.e., those that are most unique or unlike the normal flow of email traffic. Those will be the emails in the right-tail of the rank distribution. If this is the case, those values greater than the median will be those somewhat greater than the typical rank. Intuitively, this is how we want to think about recommending priority email: those with rank larger than the typical email.

Second, we know that the test data will contain email messages that have data that does not match anything in our training data. New emails are flowing in constantly, but given our setup, we have no way of updating our ranker. As such, we may want to have a rule about priority that is more inclusive than exclusive. If not, we may miss messages that are only partial matches to our features. Finally, we add a new binary column Priority to train.ranks.df indicating whether the email will be recommended as priority by our ranker.

Figure 4-5. Density of weights in training data, with priority threshold as 1 standard deviation of weights

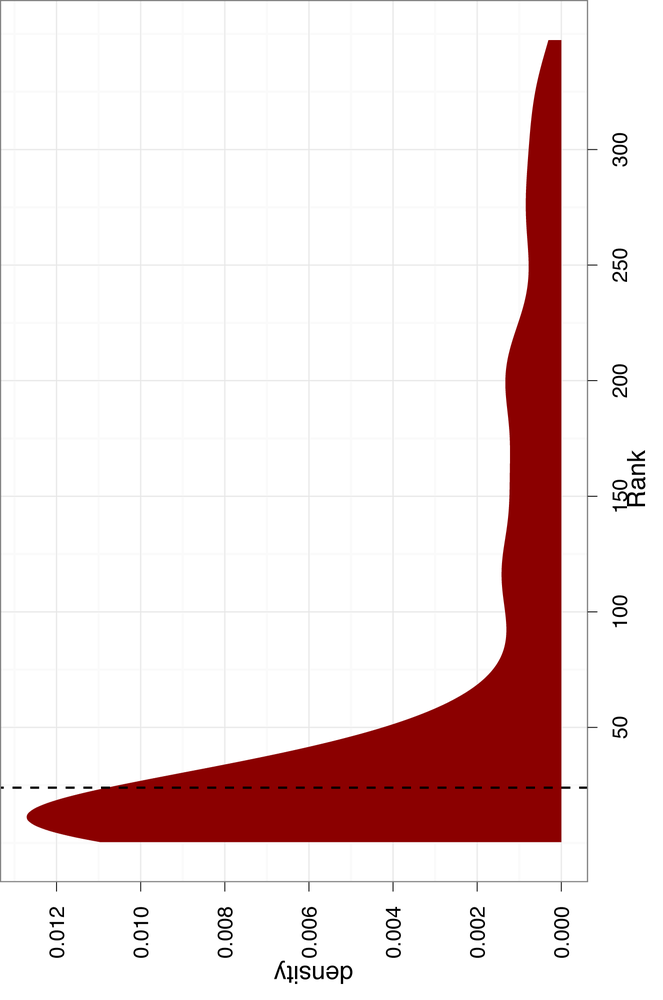
Figure 4-5 shows the density estimate for the ranks calculated on our training data. The vertical dashed line is the median threshold, which is about 24. As you can see, our ranks are very heavy-tailed, so we have created a ranker that performs well on the training data. We can also see that the median threshold is very inclusive, with a large portion of the downward sloping density included as priority email. Again, this is done intentionally. A much less inclusive threshold would be to use the standard deviation of the distributions, which we can calculate with sd(train.ranks.df$Rank). The standard deviation is about 90, which would almost exactly exclude any emails outside of the tail.

Figure 4-6. Density of weights for test data overlaid on training data density

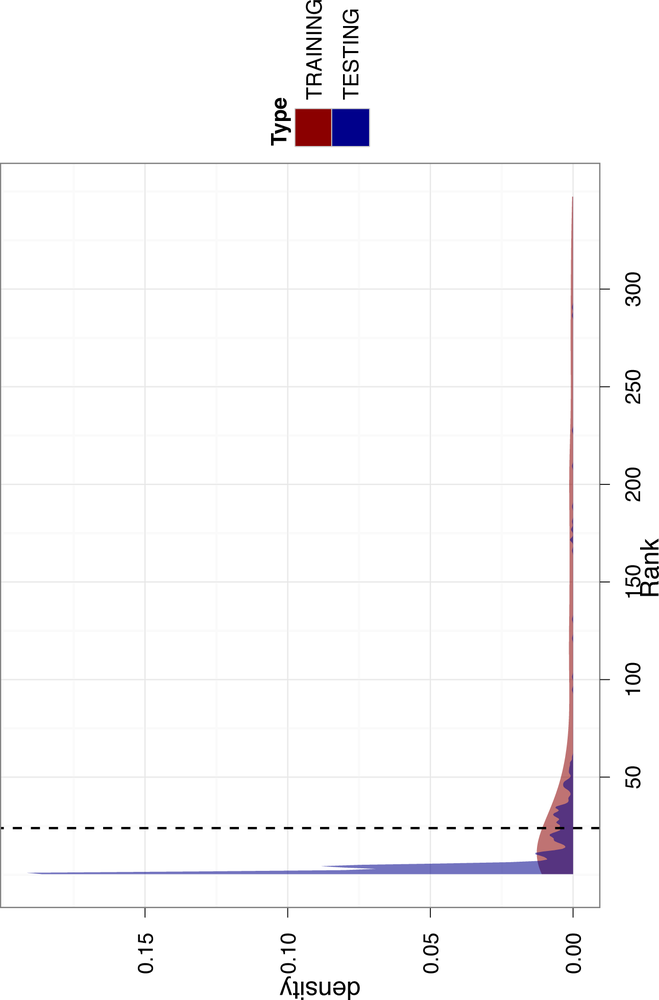
We will now calculate the rank values for all of the emails in our test set. This process proceeds exactly the same way as it did for our training data, so we will not reproduce the code here to save space. To see the code, refer to the “code/priority_inbox.R” file included for this chapter at about line 308. Once we have calculated the ranks for the test data, we can compare the results and see how well our ranker did on new emails.

Figure 4-6 overlays the density of ranks from the test data on the densities in Figure 4-5. This illustration is very informative regarding the quality of our ranker. First, we notice that there is much more density in the test data at the very low end of the distributions. This means that there are many more emails with a low rank. Additionally, the test density estimate is much less smooth than the training data. This is evidence that the test data includes many observations not in our training data. Because these observations do not match anything in our training data, the ranker effectively ignores this information.

While this is problematic, we avoid disaster because we used an inclusive threshold for priority email. Note that there is still a reasonable amount of density for the test data to the right of the threshold line. This means our ranker was still able to find emails to recommend as important from the test data. As a final check, let’s actually see which emails our ranker pushed to the top.

Warning

There is an inherent “unknowable” quality to creating a ranker of this type. Throughout this entire exercise, we have posted assumptions about each feature we included in our design and attempted to justify these intuitively. However, we can never know the “ground truth” as to how well our ranker is doing, because we can’t go back and ask the user for whom these emails were sent if the ordering is good or makes sense. In the classification exercise, we knew the labels for each email in the training and test set, so we could measure explicitly how well the classifier was doing using the confusion matrix. In this case we can’t, but we can try to infer how well the ranker is doing be looking at the results. This is what makes this exercise something distinct from standard supervised learning.

Table 4-1 shows the 10 newest emails in test data that have been labeled as priority by our ranker. The table is meant to mimic what you might see in your email inbox if you were using this ranker to perform priority inbox over your emails with the added information of the email’s rank. If you can excuse some of the somewhat odd or controversial subject headings, we’ll explore these results to check how the ranker is grouping emails.

Table 4-1. Results of priority inbox testing

Date	From	Subject	Rank
12/1/02 21:01	[e-mail]	RE: Mercedes-Benz G55	31.97963566
11/25/02 19:34	[e-mail]	Re: Men et Toil	34.7967621
10/10/02 13:14	[e-mail]	Re: [SAdev] fully-public corpus of mail available	53.94872021
10/9/02 21:47	[e-mail]	Re: [SAdev] fully-public corpus of mail available	29.48898756
10/9/02 18:23	[e-mail]	Re: [SAtalk] Re: fully-public corpus of mail available	44.17153847
10/9/02 13:30	[e-mail]	Re: From	25.02939914
10/9/02 12:58	[e-mail]	RE: The Disappearing Alliance	26.54528998
10/8/02 23:42	[e-mail]	Re: Zoot apt/openssh & new DVD playing doc	25.01634554
10/8/02 19:17	[e-mail]	Re: The Disappearing Alliance	56.93995821
10/8/02 17:02	[e-mail]	RE: The Disappearing Alliance	31.50297057

What’s most encouraging about these results is that the ranker is grouping threads together very well. You can see several examples of this in the table, where emails from the same thread have all been marked as priority and are grouped together. Also, the ranker appears to be giving appropriately high ranks to emails from frequent senders, as is the case for outlier senders such as [e-mail] and [e-mail]. Finally, and perhaps most encouraging, the ranker is making messages priority that were not present in the training data. In fact, only 12 out of the 85 threads in the test data marked as priority are continuations from the training data (about 14%). This shows that our ranker is able to apply observations from training data to new threads in the test data and make recommendations without updating. This is very good!

In this chapter we have introduced the idea of moving beyond a feature set with only one element to a more complex model with many features. We have actually accomplished a fairly difficult task, which is to design a ranking model for email when we can only see one half of the transactions. Relying on social interactions, thread activity, and common terms, we specified four features of interest and generated five weighting data frames to perform the ranking. The results, which we have just explored, were encouraging, though without ground truth, difficult to test explicitly.

With the last two chapters behind us, you’ve worked through a relatively simple example of supervised learning used to perform spam classification and a very basic form of heuristic-based ranking. We hope the experience has piqued your interest in machine learning.

---

^[8] Put more simply, this is the assumption that users are not acting on emails that were harder to identify as ham than those that were easy.