March 2012
Beginner
304 pages
6h 32m
English
APPENDIX B
Taylor Expansions
A Taylor series expansion can be used to provide approximations to a function. Given a function f(x), assuming the necessary derivatives exist, we can define the Taylor series:
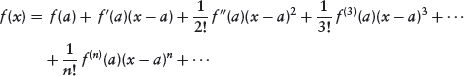
where f′, f″, and f(3) are, respectively, the first, second, and third derivatives of f(x) with respect to x.
We can talk about an nth order Taylor series expansion, which would extend to the nth term,
As an example, take the exponential function. The corresponding Taylor series expansion is:
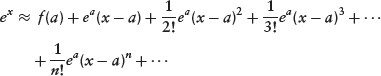
An obvious choice for a is a = 0, which implies ea = 1. In this case, we say that we are expanding ex around zero. The expansion then simplifies to:
Table B.1 shows the first few approximations for ex, expanded around zero, for various values of x:
TABLE B.1 Taylor Approximations for ex
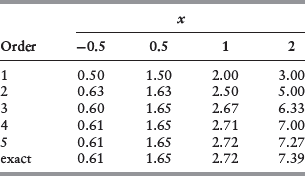
The last row is the exact value of the function, which would be equal to the infinite expansion. Notice that as we add more terms, the approximation gets closer and closer to the real value. Also notice that ...
