Matrix Differential Calculus with Applications in Statistics and Econometrics, 3rd Edition

Chapter 2Kronecker products, vec operator, and Moore‐Penrose inverse

1 INTRODUCTION

This chapter develops some matrix tools that will prove useful to us later. The first of these is the Kronecker product, which transforms two matrices A = (a_ij) and B = (b_st) into a matrix C = (a_ijb_st). The vec operator transforms a matrix into a vector by stacking its columns one underneath the other. We shall see that the Kronecker product and the vec operator are intimately connected. Finally we discuss the Moore‐Penrose (MP) inverse, which generalizes the concept of the inverse of a nonsingular matrix to singular square matrices and rectangular matrices.

2 THE KRONECKER PRODUCT

Let A be an m × n matrix and B a p × q matrix. The mp × nq matrix defined by

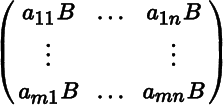
is called the Kronecker product of A and B and is written A ⊗ B.

Observe that, while the matrix product AB only exists if the number of columns in A equals the number of rows in B or if either A or B is a scalar, the Kronecker product A ⊗ B is defined for any pair of matrices A and B.

The following three properties justify the name Kronecker product:

(1)

(2)

if A + B and C + D exist, and

(3)

if AC and BD exist.

If α is a scalar, then

(4)

Another ...