Modern Control System Theory and Design, 2nd Edition

6.13.  CLOSED-LOOP FREQUENCY BANDWIDTH AND CUTOFF FREQUENCY

Let us consider the closed-loop frequency response shown in Figure 6.46 and 6.51b so that we can define the closed-loop frequency bandwidth and cutoff frequency. We define the bandwidth of a closed-loop control system in a manner similar to other electronic equipment such as amplifiers. The bandwidth of a closed-loop control system is defined as the frequency range where the magnitude of the closed loop gain does not drop below −3 dB as shown in Figure 6.54. Therefore, the bandwidth of the control system, ω_B, is defined to be that frequency range in which the magnitude of the closed-loop frequency response is greater than −3 dB. The frequency ω_B is defined as the cutoff frequency. At frequencies greater than ω_B, the closed-loop frequency response is attenuated by more than −3 dB.

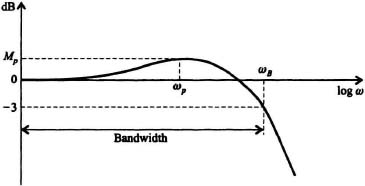
Figure 6.54   Closed-loop frequency response of a control system indicating the bandwidth and the cutoff frequency, ω_B.

The question arises as to the desired bandwidth and cutoff frequency of a control system. We would like to have a very large bandwidth so that we can reproduce the input signal (external forcing function) very accurately. Unfortunately, very large bandwidths pass high-frequency noise which can be a detriment to the control-system performance. Therefore, there are conflicting requirements on the bandwidth and cutoff frequency, ...