Multivariate Time Series Analysis and Applications

8Space–time series models

As indicated in Chapter 1, although the ordering of a time series is usually through time, it may also be ordered through space. If distances of spaces between observations are equal, the time series models and methods discussed earlier are equally applicable. However, in practice, we often see the phenomenon where regular time series are observed in different regions, and the point of interest is the study of the spatial patterns of these series. For example, in studying a traffic pattern of a certain location, traffic flow data is collected at constant intervals of time not only at that location but also at neighboring locations. In studying the prices of a certain commodity in a city, we not only want to study the price series of that commodity in that city but also the prices of the same commodity in nearby cities. In this chapter, we will present methods and models that can be used to describe spatial time series that are related to both time and space.

8.1 Introduction

One way to model the space–time series is to treat them as a vector time series where the ith component corresponds to the ith location. Thus,

(8.1)

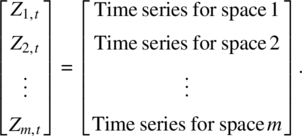
One can use the methods that were introduced in Chapter 2 to construct a vector autoregressive moving average VARMA(p,q) model or a vector autoregressive VAR(p) model for the series and use it to forecast and make inferences.

Alternatively, ...