Theory of Computation

3.2   NONDETERMINISTIC FINITE AUTOMATA

The FA formalism provides us with tools to finitely define certain languages: Such a language—defined as an L(M) over some alphabet A, for some FA M—contains a string x iff there is an accepting computation

or, equivalently an accepting path within the FA (given as a flow diagram) whose labels from left to right form x.

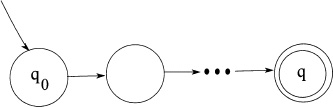
The computation (1) above, equivalently, the path labeled x within the FA, are uniquely determined by x since the automaton’s δ—the transition relation—is a total function.

Much is to be gained in theoretical flexibility if we relax both the requirements that δ is single-valued (a function) and total.

This gives rise to a nondeterministic model of finite automata, a “NFA”, that may accept a string in more than one ways, that is, there may be more than one distinct paths from q₀ to an accepting state q, each labeled by the same string x.

Indeed, even more flexibility is attained if we also allow “unconditional jumps“ from one state to another, such as

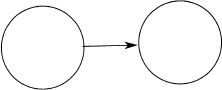
which, in the first approximation, will have unlabeled edges as above. However, in order to retain the central property that we may “read off” what string is accepted by any given ...