12.7 ROUNDOFF NOISE CALCULATION IN LATTICE FILTERS
In addition to the computation of K and W matrices based on the state variable description method, roundoff noise of lattice filters can be conveniently computed by the method proposed in [5]. This method is based upon the Schur algorithm and the transposition theorem [1],[12] and is explained in this section. Roundoff noise properties of the scaled-normalized and the reverse scaled-normalized lattice filters are also compared.
12.7.1 Roundoff Noise Computation Using Transposition Theorem
To compute the output roundoff noise, the transfer functions from the internal nodes to the output node are needed and can be found by the transposition theorem. According to the transposition theorem, the transfer functions from input to the internal nodes of transposed graph are also the transfer functions from those corresponding internal nodes to the output node in the original graph. Fig. 12.24 shows a module of the transposed graph of scaled-normalized lattice filter. (For notational convenience, superscripts are omitted. Also, using (12.79), the following notations are used: k = σ20 = − σ02,
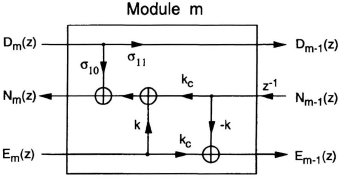
Fig. 12.24 Module m of transposed graph of the scaled-normalized lattice filter.
![]()
From the transposed graph, the following equations can be derived: ...
Get VLSI Digital Signal Processing Systems: Design and Implementation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

